Hi everyone,
Here’s my first and hopefully not last post on ethresear.ch
I would love to hear your thoughts on my proposed mechanism. I’m sure there are things I’ve missed.
For a bit of a background, I am just finishing my MS through Arizona State University and a part of my project was designing a governance mechanism for filtering proposals and requests for funding coming into a DAO. The context of my research is a non-profit “Charity DAO” which anyone can requests funds from for social impact projects. However, I see the governance model as more widely applicable to DAOs and limiting the role of trusted curators.
My governance mechanism is a bond model which requires anyone submitting a proposal and requesting funds to post a bond which will be returned to them if the proposal is successful and forfeit otherwise. This mechanism has been inspired by the ARES protocol (ares.sh). However, to me, a limitation of that protocol is a static 100 Ether bond that can only be adjusted by voting every six months. I wanted to design a dynamic bond whose size would be appropriate to its intended use and which will dynamically adjust itself based on information available in the system as opposed to voting.
There are directly measurable metrics that come with each proposal that can be used to evaluate it and calculate an appropriate bond. The most readily available metrics are the amount of funding the project is asking for, the amount of total funding available in the system (supply), and the amount of total funding requested by all pending proposals (demand). This also gives us, by proxy, the information on the proportion of total available funding a given proposal is requesting. Lastly, we can also include a reputation score (a reputation framework was a separate part of my project which I’m not going to get into here, but let’s just say that’s really the hard part so if anyone has expertise and resources for decentralized reputation system design, I’d love to hear your thoughts)
So in the bond model, we have the following variables:
B = Bond required for posting a proposal B(F, F_{L} , R, \Omega )
F = Amount of funding requested
F_{L} = Funding Request Limit agreed on by stakeholders below which no bond deposit is required. This is aimed to alleviate monetary and administrative burden for small proposals
R = Reputation ranges between 0 and 1
\Omega = DSR = Demand Supply Ratio
DSR(FS, FD) = \frac{F_{D}}{F_{S}}
F_{S}= Supply of funding (amount held by the DAO)
F_{D}= Demand for funding (outstanding amount requested)
Without further ado, here is the actual bond mechanism and I will explain the design principles and goal of the mechanism below. I will also include some sample visualizations of how the bond behaves. (Turns out I can only include one image and two links in the post, so the files are here: GitHub - Tomasvrba/DAO-bond-model-files)
\displaystyle \ B = \begin{cases} \quad 0 & \quad F \leq F_{L}\\ \frac{F}{( F^{\frac{1}{3}}R )^{\sqrt{\frac{1}{\Omega}}}} & \quad F > F_{L} \end{cases} \
The general design principles here are:
-
The bond size should rise as amount of requested funding rises. This is represented by F in the numerator of the bond model.
-
The bond should however not rise in such a way to make large projects prohibitively expensive to propose. Thus the size of the bond should rise, but it should rise at a decreasing, rather than increasing or linear rate. This is where the deflationary F^{\frac{1}{3}} in the denominator comes from.
-
The bond should also rise if there is too much demand for or not enough supply of funding. That is, if proposals are requesting more funding than is available, the bond for new proposals should automatically rise to discourage new submissions. Vice versa, if supply starts exceeding demand, the bond should decrease to incentivize more proposals.
-
Theoretically, a bond that increases at a decreasing rate of change could be viewed as a punishment for requesting smaller amounts whose bonds are disproportionately larger. It could also be viewed as an incentive for proposals to be pooled together to request larger funding amounts, as opposed to submitted separately. Here, the supply limitation should work well enough as a guard against large requests exceeding total supply. When the supply of funds is fixed or limited, the supply limitation should act as a disincentive to submitting funding requests that are too large. In other words, it is not always the case as that larger requests should require a proportionately smaller bond. The bond size behavior is very dependent on the supply of funding as well. The incentives above are handled by the \sqrt(\frac{1}{𝛺}) in the power of the denominator
-
Lastly, Reputation R which in our reputation model is on a [0,1] scale should work in conjunction with the other variables to make it affordable for agents with low reputation to still propose projects and build reputation, but to disincentivize them from requesting excessive amount of funding given their limited trustworthiness. This is why proposals below a certain amount may not require any bond at all as represented by the piecewise function. R in the denominator produces such an incentive for agents with low reputation to either build reputation first by voting and evaluating other projects, or requesting funds F < FL for which there is no bond required and build reputation that way.
Here are some visualizations for a better idea of how the bond changes with different variables:
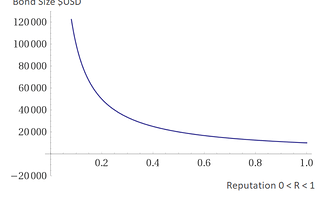
Effect of varying Reputation, holding F and \Omega constant
Here we see the non-linear relationship between bond size and reputation. With very low reputation (R<0.2) the posted bond is very expensive relative to the total amount of funding requested. Therefore, agents who request funds are incentivized to either build reputation first by voting and evaluating other projects, or requesting funds F < F_{L} for which there is no bond required and build reputation that way.
Effects of varying Supply and Demand against Reputation, holding F constant
Effects of varying supply and demand
Here we see the effects of varying supply and demand. Specifically, we see that as demand outpaces supply (by a factor of two in the example above) the required bond sizes for submitting a proposal rise, disproportionately affecting those with lower reputation, thus discouraging new entries into the system and spamming of proposals. The opposite is true for when supply is larger than demand. The required bond becomes much cheaper for everyone and only those with really low reputation (R<0.1) still face a significant barrier to entry.
Effects of varying Requested Funding, holding R and \Omega constant
See VaryingRequestedFunding.png
We see that at this scale, even though bond size is designed to increase at a decreasing rate, reputation plays a highly important role. Looking at a funding request of $1B, an agent with baseline reputation of 0.2 would have to deposit a $5,000,000 bond, while an agent with 1.0 reputation deposits a bond of only $500,000. A relatively small amount given the amount of funding requested.
Effects of varying Requested Funding, with a limited fixed supply of funds, holding R constant
See FixedSupply.png
The supply limitation should work well as a guard against large requests exceeding total supply as seen above. The figure shows what happens when the supply of funds is fixed or limited as opposed to maintaining a dynamic \Omega ratio which was the assumption in previous models. We are looking at an example of funding requests between $0 and $100,000 and we can see that by fixing the supply of funds at $80,000 we change the bond size function to increase exponentially. The supply limitation thus acts as a disincentive to submitting funding requests that are too large. In other words, it is not always the case that larger requests always require a proportionately smaller bond. The bond size behavior is very dependent on the supply of funding as well.
Looking forward to everyone’s feedback.
Tom