by: Davide Rezzoli (@DavideRezzoli) and Barnabé Monnot (@barnabe)
Many thanks to Yoav Weiss (@yoavw) for introducing us to the problem, Dror Tirosh (@drortirosh) for helpful comments on the draft, and the 4337 team for support. Reviews ≠ endorsements, all errors are the authors’ own.
This work was done for ROP-7
Transaction fee mechanisms have become the workhorse models to understand the intermediation of block producers between users wishing to transact and “the chain” (or “the protocol”) which users transact on. Given the ability to use some of the supply provided by the chain, the block producers must arbitrate which users will have ability to use the scarce resource of on-chain execution, and at what cost. On Ethereum, for the question of cost, block producers are constrained by the EIP-1559 fee mechanism, which dynamically sets a reserve price block-to-block, called “base fee”. The base fee is a price, expressed per units of gas, which a user transaction must pay to be included and executed. The user may provide so-called “priority fees” beyond the base fee, to further incentivise the block producers in times of congestion.
In this note, we investigate the question of embedded fee markets, i.e., fee markets which “live” within other fee markets. This question was discussed in a different context in a recent paper by Maryam Bahrani, Pranav Garimidi and Tim Roughgarden, “Transaction Fee Mechanism Design in a Post-MEV World”. In this paper, the authors model the use of searchers, further intermediating access to the chain between users and block producers. Block producers receive “hints” from searchers, embodied by atomic bundles of transactions to be included by the chain. The fee market of searchers is driven by the maximisation objective of a quantity known as MEV, or maximal extractable value.
In our setting, users wish to access the chain but do not express their demand using protocol-legible transactions. Instead, users produce “operations”, to be bundled by entities known as “bundlers”, who then originate a protocol-legible transaction packing the operations together towards execution. Thus, to the EIP-1559 fee mechanism, bundlers are the users of the chain, yet the actual users must first obtain inclusion in the bundle of a bundler before they may gain inclusion to the chain. In other words, we may see this setting as part of the larger question of block co-creation, which arises with (partial) builders/searchers as well as inclusion lists.
Our hope is for these dynamics to be as transparent as possible, such that there is not either more cognitive overhead or opportunities for the user to be unduly exploited by the bundler, compared to going on-chain directly. We hope for even stronger results, cases where indeed the users benefit from the bundler intermediation, when amortised costs allow users to enjoy greater welfare.
To investigate the distinction between direct fee markets and their embedded (sub-)mechanisms, we must precise the economic constraints which a bundler abides by. In the following section, we offer a simple model of the bundler cost function motivated by the practice, in particular bundlers participating in the ERC-4337 protocol, which we briefly recapitulate.
Model
Bundling in ERC-4337
A user wishing to perform some activity on-chain via bundlers issues a User Operation (UserOp, or operation). This UserOp is emitted from the user’s wallet, e.g., after interacting with a DApp. Once the UserOp is broadcast, some bundler receiving the operation may decide to include it in a bundle. A bundle is an “externally-owned account” (EOA) meta-transaction, which writes the data of the included UserOps in its bundle.calldata field. The bundler issues the bundle towards inclusion in a block by a block producer (we discuss the relation between bundler and block producer in a future note).
Once the bundle is included in the block, and the block makes its way to the chain, the bundle is executed along with other transactions in the block. Essentially, the bundle execution steps are as follows:
- Pre-verification: A bundler’s EOA transaction will consume 21,000 gas, and the call to the EntryPoint contract will set up key variables to keep track of the execution of the operations in the operation loop.
- Operation loop: For each operation included in the bundle, the following two steps take place:
- Verification step: UserOps perform operations containing a verification step, which is encoded in a “smart contract wallet” deployed initially by the user (during an initial UserOp). The verification step may simply check a signature, or perform more complex operations to “grant” the right for the UserOp to proceed with its execution. The verification step is metered by
op.verificationGasLimit. - Execution step: The core of the UserOp, the execution step performs the operation described in
op.callData. This step is also metered, usingop.callGasLimit.
- Verification step: UserOps perform operations containing a verification step, which is encoded in a “smart contract wallet” deployed initially by the user (during an initial UserOp). The verification step may simply check a signature, or perform more complex operations to “grant” the right for the UserOp to proceed with its execution. The verification step is metered by
As is made clear by the previous decomposition, the pre-verification step is executed once, offering the possibility to amortise the pre-verification costs across all included users. When the bundle is executed, all costs (e.g., block.basefee + priority fees paid by the bundler to the block producer including them) are charged to the bundler, who must ensure that user operations compensate her enough for the costs incurred. We make these statements precise in the following section.
Fee market model for bundles
We attempt to remain consistent with classic fee markets models. A user t who wishes to emit an operation has some value v_t for the execution of the operation. We assume all operations to have the same size S (i.e., same gas used for the verification and execution steps), and we thus express all quantities as prices per unit of gas.
Users express their wish to be included by emitting a bid b_t along with their operation. For now, we do not assume a specific grammar for the user to express their bid for inclusion, e.g., the ability to express a max fee and priority fee along with their operation, as they would with EIP-1559. User operations are collected in a mempool \mathbf{M}, representing the pending status of these operations until inclusion.
The EIP-1559 fee market exposes a reserve price r known as “base fee”, which bundlers must incur when their bundle is executed. If the bundle contains n operations, the bundler must then expense at least n \times S \times r. Additionally, since the bundle consumes “pre-verification gas”, say, some quantity F, the bundler will additionally pay F \times r. The operations included in the bundle are given by the set \mathbf{B}.
Bundler cost functions
We now consider the costs incurred by bundlers for the inclusion of their bundles in the block.
On-chain cost function: A bundler issuing bundle \mathbf{B} when the base fee is r expends a cost:
The bundler problem mirrors the block producer problem expressed in [Roughgarden 2021]. There, the block producer had to ensure the provision of some value \mu compensating her for the cost of including an additional transaction to their block (e.g., \mu may compensate for the extra load of the block, which delays its propagation and thus increases re-org risk). The block-level fee market must then ensure that the block producer is at least compensated for the total cost n \times S \times \mu, should the block producer include n transactions in their block. The bundler-level fee market will require to at least compensate the bundler for exogenous costs C_\text{on-chain}(\mathbf{B}, r) they incur from the larger fee market they are embedded in.
ERC-4337 offers the possibility amortise costs beyond sharing the pre-verification gas costs. Should all operations employ the same signature scheme for their verification step, the signatures of these operations may be aggregated by the bundler, such that instead of verifying on-chain n signatures, a single signature may be verified. In this case, the bundler cost function will need to account for the off-chain costs which the bundler incurs when performing the aggregation. In the following, we make the assumption that such costs are linear in the number of operations, a similar assumption to [Wang et al., 2024], at a marginal cost \omega.
We also account for the reduced gas consumption of each operation, due to savings from the aggregation. When aggregated, operations are not required to publish their signature, but they do require an additional pairing operation. On chains where calldata cost is expensive, but pairing operations/computation are cheap, aggregation thus provides per-operation savings. In this case, we denote by S' < S the reduced size of a transaction. We also need to account for the increased pre-verification gas use F' > F, which now contains the publication and verification of the single on-chain aggregated signature.
Aggregated cost function: A bundler issuing bundle \mathbf{B} with aggregated signatures when the base fee is r expends a cost:
In this note, we will not go further, but one may also consider the data publication costs which a bundler may need to expend when their bundle settles on a rollup. We suggest two ways of modelling this and leave this question for future work:
- Either the bundler herself is responsible for data publication (e.g., as a sequencer), and thus requires to obtain from users the necessary amount of funds to pay eventual data publication costs.
- Or the bundle-level fee market is embedded in a larger batch-level fee market, via which the rollup exposes to rollup users (including the bundler) the amount they are required to pay due to congestion (e.g., a base fee) and eventual data publication costs. In this case, the rollup is responsible for balancing their own future costs with their present revenues.
Revisiting fee market quantities
We may now formally express the relevant concepts for the bundle-level fee market, deriving them straightforwardly from previous literature, while taking the embedding into account.
Bundle-level allocation rule: A (bundle-level) allocation x decides the set of user operations which the bundler includes in their bundle, given the current mempool \mathbf{M} and the base fee r.
Bundle-level payment rule: Given the set of selected operations \mathbf{B}, a payment rule assigns to each included user a fee:
User utility function: u_t(b_t) = v_t - p_t(\mathbf{B})
In principle, we could allow for the existence of a burning rule q_t(\mathbf{B}) expressing the fact that the bundler may not receive the totality of all included user payments. We do not consider it in this note however.
(Myopic) bundler utility function: u(\mathbf{B}, r) = \sum_{t \in \mathbf{B}} p_t(\mathbf{B}) - C(\mathbf{B}, r)
A bundle-level TFM (x, p) is incentive-compatible for myopic bundlers (MBIC) if, for every mempool \textbf{M} and base fee r, a myopic bundler maximises its utility by following the suggestion of the allocation rule x (i.e., setting \textbf{B} = x(\textbf{M}, r)).
Forming multiple bundles
In the preceding section, we’ve only considered the possibility for the bundler to issue a single bundle. However, we may be interested in the possibility for the bundler to make more than one bundle out of the operations available in the mempool. Given the mempool \mathbf{M}, let P(\mathbf{M}) represent the set of partitions of the mempool, assigning each operation to a single bundle (we may assume that for each partition, there is a set indexed 0 which contains all the operations not assigned to a bundle for inclusion). The allocation rule then returns the index of the set in the partition to which the operation is assigned.
We can write the set of bundles output by the partition x(\textbf{M}, \beta) as \mathcal{B}(x(\textbf{M}, r)). Intuitively, these bundles are made up from the operations which do not belong to the set indexed 0. Given a set of bundles \mathcal{B}, the payment rule is then:
The user utility function becomes:
and the bundler utility function becomes:
The bundler game
Inclusion of transactions in blocks must remunerate some quantity \mu to the block producers, which is assumed to be linear in the transaction size in e.g., [Roughgarden, 2021]. This quantity denotes the opportunity cost for the block producer to add an extra transaction to their block, e.g., increasing their gossiping delay and thereby increasing their chances of the block getting re-orged. In Proof-of-Stake, even though the protocol’s schedule allows for enough time to propagate a full block, timing games have induced “last-second” propagation dynamics which have once again made this \mu parameter relevant.
In any case, we may observe that the cost-sharing problem at block-level and at bundle-level are very different. At block-level, a transaction need not know what else is going on inside the block to devise its inclusion bid according to EIP-1559 (it may want to know what is going on with respect to MEV [Bahrani et al., 2024], but we’ll consider this a separate issue for now). At bundle-level, bundle overhead costs are no longer linear in the number of transactions, but a fixed overhead may be amortised by many transactions. Further, should the aggregation cost of the user operations be non-linear in the number of transactions (e.g., some proofs are effectively sub-linear in the size being proven), offering the possibility to amortise the total cost over many users.
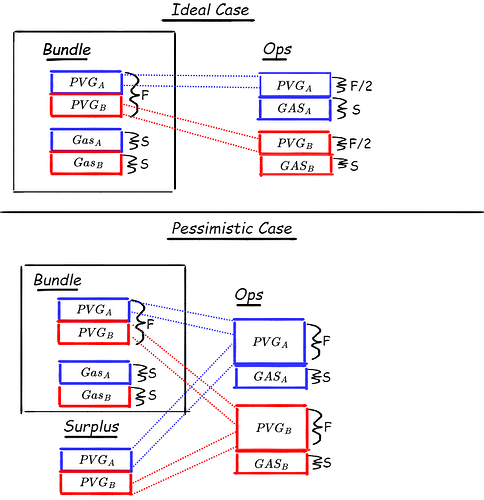
This leads to the following game: The bundler wishes for users to place their bids as if they were bidding for the worst case, where the user is alone in the bundle and must compensate by themselves the full overhead gas F. Practically, the user would be faced with the problem of setting three relevant parameters on their operation:
op.maxPriorityFeePerGasandop.maxFeePerGasmay be set according to the heuristics a user would use under EIP-1559, i.e., given some estimate amount of gas their operation plans to consume, the user would set these attributes to calibrate how much they are willing to pay in the worst case (maxFee) and how much they are willing to top up in order to pay the eventual block producer (maxPriority). But how should the user estimate the gas?op.preVerificationGasis an attribute of the UserOperation which must be set to indicate the amount of “extra gas” the user’s operation plans to consume. In our model, we let F denote this “fixed gas overhead”. If n users were included in the bundle, each user ought to setpreVerificationGas = F / n. However, should the user prepare their operation with a worst-case scenario in mind, they would setpreVerificationGas = F.
preVerificationGas is then the principal vector via which users mediate their bid and attempt to account for the amortisation of costs by the bundler. Assume n users do come to the market with their operations, and all are convinced by the bundler to bid in the worst-case of being alone in the bundle. We’ll also assume that the users are setting their maxPriorityFeePerGas to zero for the sake of this example. Then these n users are all setting preVerificationGas = F, and the bundler is able to output a bundle remunerating them with:
while they must incur a cost:
once they publish the bundle bundling all n operations together in a block. This yields the bundler a profit \pi = (n-1) \times F \times r.
This situation may be represented by a two-stage game, where the users first produce their user operations, and the bundler subsequently decides to bundle them. We assume that users do not possess information about the current amount of pending users, and so are unable to estimate the bundler’s true ability to amortise their fixed costs.
In the first stage, users send their operations, which commit to their attributes such as preVerificationGas. In the second stage, the bundler having received all user transactions decides to output a bundle or set of bundles. Interestingly, even if the users know how many other users will play in the first stage, i.e., even if n is common knowledge across all users, the bundler may be able to force the users into setting the worst-case preVerificationGas = F by threatening to play \mathcal{B}_\text{pessimistic} = \{ \{ 1 \}, \{ 2 \}, \{ 3 \}, \dots, \{ n \} \}, i.e., threatening to keep every user in their own separate bundle and charging them the maximum amount gas F.
Note that this threat may not be credible, as users would expect the bundler to prefer playing \mathcal{B}_\text{ideal} = \{ \{1, 2, 3, \dots, n \} \}, i.e., output a single bundle with all operations included there, realising \pi. However, users may not have access to the true value of n, and thus they are unable to set their preVerificationGas in a way that forces the bundler to ideally bundle all of them.
An extension of this model may consider the Bayesian case, where the users have access to a distribution over n, i.e., they may anticipate some random variable n users to show up at any given time step, according to some distribution (e.g., Poisson arrivals), even if they do not know in advance the outcome of the random variable. This may lead to inefficient outcomes, as the following example shows:
Alice expects 9 other users to show up besides herself, and so she sets her
preVerificationGasto 1 as she knows F = 10. Alice’s value and the value of all other users is compatible with them settingpreVerificationGas = 3, but she attempts to pay the least amount possible for her inclusion. As it turns out, only 5 users appear on the market, who have all set theirpreVerificationGasto 1 too. The bundler will not be compensated forF = 10units of gas, thus the bundler does not output a bundle and users receive 0 utility. This is obviously suboptimal, as the users could have all setpreVerificationGas = 2for instance and receive 1 utility (the maximumpreVerificationGasthey were willing to set minus the actualpreVerificationGasthey paid to be included).
Future work
As the bundler game shows, an allocation problem faces the user wishing to be included by the bundler. In the next note, we will address different approaches to recovering “good UX” for the user to prevent them from overpaying a bundler who is better informed about the demand for its bundle capacity. The next exploration will require an understanding of the market structure tying users, bundlers and builders/block producers together.