Abstract
We present a new algorithm for order book DEX “LOBSTER - Limit Order Book with Segment Tree for Efficient oRder-matching” that enables on-chain order matching and settlement on decentralized smart contract platforms. With LOBSTER, market participants can place limit and market orders in a fully decentralized, trustless way at a manageable cost.
Introduction
Implementing an order book on the Ethereum virtual machine (EVM) is a non-trivial task. Unlike centralized exchanges (CEX) that can iterate over orders to settle trades or iterate over several price points to handle large market orders, on EVM, such operations can reach the networks gas or time limitations and fail to go through. To save the user from excessive gas fees and allow orders to be made reliably, any operations that iterate an arbitrary number of times must be constrained and optimized.
When implementing an on-chain order book, we had to solve two major challenges regarding arbitrary iteration.
- Iterating over orders to settle.
- Iterating over price points to fill a large market order.
Through the thoughtful use of traditional data structures that we modified and rewrote from scratch to optimize gas fees, we overcame these two bottlenecks and successfully implemented a gas-feasible order book.
1. Iterating Over Orders to Settle
Manual Claiming
Settling an order consists of giving both the taker and the maker their proceeds from the trade. While there is only one taker in that trade, there is no limit to the number of makers that need to be paid. Iterating over a list of makers would be problematic on the EVM and may cost even cause the transaction to time out and fail if the list is long enough. The only workaround to this problem is to handle the maker’s portion of the settlement in a separate transaction that the maker would call themselves.
Knowing When to Claim via Claim Range
Without the takers bothering to alert the makers that their orders are claimable, the task of checking is left to the makers themselves. This can be done by comparing the unaccounted accumulative sum that has been taken from an order queue with the “claim range” of an order, a value derived by adding the order sizes in an order queue. The key takeaway here is that with the introduction of manual claiming, the burden of iterating over orders is simplified to a problem of finding the sum or partial sum of a constantly updating queue of orders.
(Finding the sum of an array or subarray of orders might seem like a problem that involves iteration. However, as we will later discuss, it can also be solved quite elegantly by using a segment tree, and even better by using a Segmented Segment Tree.)
Order Claim Range
The order claim range is derived from the following equation.
Total Claimable Amount
We will call the “unaccounted accumulative sum that has been taken” mentioned earlier the total claimable amount. When someone takes an order from an order queue, the total claimable amount is increased by that amount. If anyone claims an order, the total claimable amount is decreased by the amount claimed. In other words, it is the amount taken that has not been accounted for by claiming it.
Comparing Order Claim Range with Total Claimable Amount
Now to put these two values to use. The equations below show if and by how much an order can be claimed.
Let T = \text{total claimable amount}.
There are three different states an order claim interval [\alpha, \beta] can be concerning T.
- \beta < T\text{, the order is completely claimable.}
- \alpha < T < \beta\text{, the order is partially claimable and the claimable amount is }T -\alpha.
- T<\alpha\text{, the order is not claimable at all.}
In other words the claimable amount c(T, [\alpha, \beta]) = min(max(0, T - \alpha), \beta - \alpha).
Example
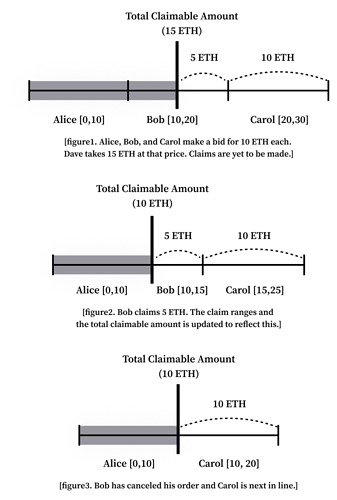
For example, let’s assume that Alice, Bob, and Carol each make a bid for 10 ETH in sequence at a certain price point. If Dave comes in to sell 15 ETH at that price point, Alice would be able to claim all 10 ETH, Bob would be able to claim 5 ETH, and Carol none at all. While this is quite intuitively true, it can get confusing when claims, partial claims, and cancels start entering the picture. By comparing the order claim range of each user with the total claimable amount, it becomes easier to track. The diagrams below illustrate this.
If Bob were to claim the 5 ETH that is currently available to claim, the total claimable amount and Bob’s unclaimed order size would decrease to reflect this.
As Bob’s order and the total claimable amount decreased, Carol’s order claim range has been affected to keep things consistent. From this, we can gain insight that a solution that holds the order claim range in memory would not be sufficient, as claiming or canceling an order would cause the code to iterate over every subsequent order to update each claim range.
If Bob became impatient and canceled his remaining order, the total claimable amount would not budge but Bob’s unclaimed order size would become zero and change Carol’s order claim range. This is good news for Carol as she does not have to wait for Bob’s order to be filled anymore for her turn to come.
Sum of Given Range
Let’s look into three different ways of getting the sum of a range and compare their pros and cons to select the best solution.
Brute Force
Simply iterating over the queue to query the sum every time can be made possible, but it would require a very hard limit on the maximum number of orders allowed on the queue. There are some implementations of EVM order books that only allow 32 orders per queue that we believe use this method. This implementation has a strong advantage over other methods in that updating an order size only requires one storage slot to be updated. However, we considered the 32 orders per queue limit too strong of a constraint to function as a fully-fledged order book.
Prefix Sum (Lookup Array)
A slightly more sophisticated approach (algorithm-wise) is using a lookup array with the sum of all the orders from the starting index to the nth order as the nth element of the array. This can make querying the sum a matter of O(1), but show horrible performance when an order is claimed or canceled since when an unclaimed order size is updated, it will require an iteration updating the lookup array. Considering how common canceling and claiming are, and how sstore can be 10 times more expensive than a sload, this version has the worst overall performance.
Segment Tree
With a segment tree, querying the sum and updating an element both take O(log(n)). The number of levels the tree supports is indicative of how expensive a query and update will be. To update an element, an update has to be made at every level of the tree. Therefore with this method, we need to constrain the number of orders per queue to make sure this number doesn’t get out of hand.
Conclusion
By using a highly customized segment tree, the Segmented Segment Tree, we successfully created a segment tree that can handle 2048 orders with just 3 storage updates. This allowed us to achieve gas fees for swaps that are on par with what the state-of-the-art AMMs, like Uniswap, have to offer. A detailed look into how the Segmented Segment Tree works will be shared in the future.
2. Iterating Over Price Points to Fill a Large Market Order
Mind the Gap!
Lower liquidity in markets can create instances where the two lowest ask price points or the two highest bid price points are not adjacent, creating a gap. This gap can become problematic when iterating over the price points to handle market orders that are filled across multiple price points. There is no reliable way to know how big these gaps are and the worst case would merit a scan through the entire list of possible prices.
Let’s assume there is an order book with 10 ETH being sold at 1000 USDC, 10 ETH being sold at 2000 USDC, and none sold at other price points. If Alice were to make a market order of 30000 USDC, buying the whole stock, after buying the 10 ETH sold at 1000 USDC, we would need to iterate over all the possible price points between 1000 and 2000, checking if there are any ETH to take. With a tick size of 1 USDC, this would mean that 1000 storage reads would take place, probably causing the transaction to fail. (If Alice were to make an order of 30001 USDC, it would iterate to the highest possible price, finding that there wasn’t enough liquidity to begin with.)
Skipping the Gap. Heap Helping Heaps
Instead of iterating through the price points in the gap, we used a heap data structure to keep tabs on all the valid price points, so we could effectively skip the gaps. A heap is a tree-based data structure where if it’s a max heap, each node is bigger than or equal to all of its children, and if it’s a min heap, each node is smaller than or equal to all of its children. We used a max heap to handle the highest current bid and a min heap to handle the lowest current ask.
By using a highly customized heap, the Octopus Heap, we successfully created a heap that can handle most cases using just one storage read or storage write. A detailed look into how the Octopus Heap works will be shared in the future.
Closing Remarks
AMMs, while possible, are not utilized in CeFi because of their poor performance in providing liquidity. They only exist in DeFi because of their passive market-making abilities, alleviating the need to constantly pay obsessive gas fees. However, as layer 2 technologies develop, the trend is projecting ever-lower gas fees, opening up a market for order books to replace swaps done on AMMs. Eventually, order books will become the preferred way of swapping assets, just like it always has been for CeFi.