Ethereum 9¾: Send ERC20 privately using Mimblewimble and zk-SNARKs
A user can enter into the magical world by depositing ERC20 tokens to Ethereum 9¾ and then sending ERC20s privately using Mimblewimble spells. Also, the user can withdraw ERC20 tokens to the muggle world by submitting proof.
TL;DR
- Technical characteristics
- It sends ERC20 using Mimblewimble protocol on zk-SNARKs.
- The commitment-nullifier scheme secures anonymity.
- It uses Pedersen Merkle Mountain Range for its data structure.
- It uses zk roll-up and also supports optimistic roll up with deterministic fraud-proof.
- Performance
- Relayers can aggregate up to 32 transactions at once.
- Current implementation consumes 147k gas for a Mimblewimble transaction.
- Etc
- Relayers can aggregate transactions and receive fees in ERC20.
- We can also use the protocol without relayers.
- Istanbul is going to enhance performance 4–5 times.
- Where’s the code?
- Here is the implementationhttps://github.com/ethereum934/eth-mimblewimble
Let’s see @ Devcon Osaka
Abstract
Using crypto money in our daily lives is still a future until we split the bill by using DAI and Metamask rather than using Venmo or, in Korea, Kakao Pay. One of the causes of this situation is the privacy problem; especially, as many people start to use ENS, we are experiencing the privacy-less world. Representatively, through Etherscan, we can quickly check an ENS owner’s ETH balance, where the money comes from, or even how much is lent from MakerDAO. It makes us hesitate to share ENS and send crypto money to each other. To solve this problem, Ethereum 9¾ comes up as a protocol to send ERC20 privately in a cost-effective way using Mimblewimble and zk-SNARKs.
Ethereum 9¾ is a construction of Mimblewimble, Pedersen hash, Merkle Mountain Range(MMR), and (optimistic) roll-up with zk-SNARKs. Using both concepts of ZCash’s commitment-nullifier scheme and Mimblewimble protocol together on Ethereum, it hides the transaction details and the token flow while guaranteeing no money is printed out of thin air. Also, Pedersen Hash and Merkle Mountain Range reduce the gas costs and allow rolling up 64 items at once.
Through this construction, it achieves 147k gas per private transaction by the optimistic roll-up which supports a deterministic fraud-proof without any data availability problem. Moreover, as relayers can aggregate transactions and accept fees in ERC20 by the Mimblewimble protocol, it is expected to see new DAOs and De-Fi products using Ethereum 9¾.
Mimblewimble for ERC20
Pedersen commitment
Mimblewimble protocol hides the transaction details using the elliptic curve cryptography, which was proposed by Tom Elvis Jedusor through the Bitcoin research channel in 2016. Mimblewimble transaction output is made up of the sum of homomorphically hidden randomness and homomorphically hidden value. That is called Pedersen commitment and is one of the lightest forms to express a TXO, which hides both value and ownership inside.
With this homomorphic encryption using ECC, we can assure that the sum of the values in the inflow TXOs equals the sum of outflow TXOs values. To get more details, please check Grin’s Mimblewimble explanation here.
Commitment-nullifier scheme for Mimblewimble
While Grin secures the privacy by having no account and the cut-through-ing, on Ethereum, we cannot prevent the tracking of the transaction flow. Although it still hides the amount of value included in the transactions, allowing the transaction flow weakens the privacy. Thus, ZCash’s commitment-nullifier scheme can be useful in severing the link between inflow and outflow.
Ethereum 9¾ computes the nullifier of Mimblewimble TXO by multiplying the TXO by the hidden randomness.
With this scheme, the contract manages the Merkle trees only storing the root values on Ethereum with zk roll-up. To spend a TXO, users can submit the nullifier instead of revealing the TXO. Further, because there is a 1:1 correspondence between y values and elliptic points on the BabyJubjub curve, we can use the y-axis values as the spent tags for nullifiers to prevent double-spending.
Zk Mimblewimble transaction
To use the commitment-nullifier scheme, we need to change the transaction structure a little bit.
-
Vanilla Mimblewimble transaction
Original Mimblewimble Transaction Kernel Excess
Schnorr signature
Fee
MetadataBody Input TXOs
Output TXOsProof Range proofs of output TXOs -
Mimblewimble for ERC20
Zk Mimblewimble Transaction for ERC20 Kernel Excess
Schnorr signature
Fee
Metadata(ERC20 address, Expiration)Body  Spent tags of input TXOs
Spent tags of input TXOs Input TXOs
Output TXOsProof Range proofs of output TXOs
 Inclusion proofs of spent tags
Inclusion proofs of spent tags
 Mimblewimble proof
Mimblewimble proof
Because it does not expose the input TXOs, it is only able to verify the Mimblewimble transaction using zk-SNARKs. Therefore, the transaction builder should submit appropriate proof to verify that the values follow the Mimblewimble protocol correctly. Also, it is necessary to submit inclusion proofs to verify that the given root properly includes the input TXOs which are homomorphically hidden by the spent tags.
zk-SNARKs friendly data structure for append-only usage
The inclusion proof with zk-SNARKs brought by the commitment-nullifier scheme becomes zk-ineffective if it uses keccak256 for its hash function to construct the Merkle tree. Therefore, it is good to have another zk-friendly and append-only usage data structure. So Ethereum 9¾ comes up with Pedersen Merkle Mountain Range.
Pedersen Merkle Mountain Range
Peter Todd proposed Merkle Mountain Range for an efficient append-only Merkle tree data structure, and Grin is now using that. In Ethereum 9¾, it uses a slightly tweaked version of MMR that utilizes elliptic curve cryptography to compute each node. It cuts off the costs for inclusion proof and roll-up proof.

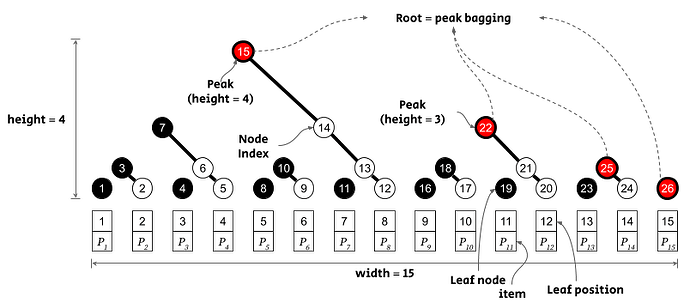
Node
: Circles in the above image. All nodes are elliptic points on the BabyJubjub curve.
Node index
: This is the number in each circle.
Width
: This is the total number of leaf items.
Leaf position
: Leaf position is the order of the leaf item. It is equal to the number in the square box.
Leaf item
: The elliptic curve points stored in the leaves, such as P_1, P_2, ...
Leaf node
: Leaf nodes are the first-floor nodes such as 1, 2, 4, 5, 8, 9, ... , 25 . A leaf node value equals a multiplication of the item point and the leaf position.
Branch node
: A branch node value equals a multiplication of the right node and the left node’s y value. If the left node is the infinity of zero, the result equals the right node.
If the left node is the infinity zero (0,1) , the result is same with the right node.
Peak
: Peaks are the nodes with red circles in the above figure. The bitmap of the MMR’s width provides the existence of a peak for each height, which corresponds to the bit index.
1 = bin'000001' # MMR of width 1 has 1 peak of h(1)
2 = bin'000010' # MMR of width 2 has 1 peak of h(2)
3 = bin'000011' # MMR of width 3 has 2 peaks of h(2), h(1)
4 = bin'000100' # MMR of width 4 has 1 peak of h(3)
5 = bin'000101' # MMR of width 5 has 2 peaks of h(3), h(1)
6 = bin'000110' # MMR of width 6 has 2 peaks of h(3), h(2)
7 = bin'000111' # MMR of width 7 has 3 peaks of h(3), h(2), h(1)
8 = bin'001000' # MMR of width 8 has 1 peak of h(4)
9 = bin'001001' # MMR of width 9 has 2 peaks of h(4), h(1)
10 = bin'001010' # MMR of width 10 has 2 peaks of h(4), h(2)
11 = bin'001011' # MMR of width 11 has 3 peaks of h(4), h(2), h(1)
12 = bin'001100' # MMR of width 12 has 2 peaks of h(4), h(3)
13 = bin'001101' # MMR of width 13 has 3 peaks of h(4), h(3), h(1)
14 = bin'001110' # MMR of width 14 has 3 peaks of h(4), h(3), h(2)
15 = bin'001111' # MMR of width 15 has 4 peaks of h(4), h(3), h(2), h(1)
Peak bagging
: This is the final root value of the total Merkle Mountain Range. In Pedersen MMR, the root equals a multiplication of the factorial of the peaks and the width, similar to the following equation:
The calculation of \Pi_{1}^{Height} Peak can be accomplished with the below procedure:
Finally, the root becomes:
zk-SNARKs circuits for Pedersen MMR
In Merkle Mountain Range, the information that we need to update an item is only the bits of knowledge about the previous peaks. Therefore, we can simplify the process using a recursive calculation to update several items.
[zk-SNARKs circuit in ./circuits/mmr/mmrRollUp16.code]
import "PACKING/split" as split
import "../ecMul.code" as ecMul
import "./peakBagging.code" as peakBagging
import "./peakUpdate.code" as peakUpdate
def main(field root, field width, field[16] xPeaks, field[16] yPeaks, field[16] xItems, field[16] yItems) -> (field):
// Check peak bagging
root == peakBagging(xPeaks, yPeaks)
// Update peaks
for field i in 0..16 do
xPeaks, yPeaks = peakUpdate(width, xPeaks, yPeaks, [xItems[i], yItems[i]])
width = width + 1
endfor
// Return peak bagging
return peakBagging(xPeaks, yPeaks)
For the efficiency, Ethereum 9¾ uses 16-bit Merkle Mountain Range which can contain up to 66,535 items. Too small of a size weakens the anonymity, and too big of size increases the cost. Accordingly, it is optimal to manage several roots of 16-bit or 32-bit MMR in parallel.
To review more detail implementations go to the following links:
Building a Mimblewimble transaction
The process of building a Mimblewimble transaction is quite similar to Grin’s process, but there are more steps to generate zero knowledge proofs additionally.
Creating a coin-base tag
Depositing ERC20 is the starting point to use Ethereum 9¾. To deposit ERC20 correctly, a user should generate a TXO with the value to deposit and a random value to use for a private key. Then, the user should generate a proof which guarantees the spent tag is the nullifier of a hidden TXO, and the TXO’s value is between the given range to avoid overflows in zk-SNARKs circuits.
[Sample Python code]
from py934.mimblewimble import Output
# Trying to deposit 1000 DAI
txo = Output.new(1000)
"""
txo.r = 193712389187391823781 # random
txo.v = 1000
"""
tag = txo.tag
"""
nullifier = txo.r * txo
tag = nullifier.y
"""
deposit_proof = txo.deposit_proof
"""
public_values = [tag]
private_values = [txo.r, txo.v]
"""
ethereum934.functions.depositToMagicalWorld(
erc20_address,
tag,
txo.v,
deposit_proof.a,
deposit_proof.b,
deposit_proof.c,
).transact({'from': alice})
Depositing ERC20 with the generated coin-base
[Solidity code in ./contracts/Ethereum934.sol]
/** @dev Deposits ERC20 to the magical world with zkSNARKs.
* @param erc20 Address of the ERC20 token.
* @param amount Amount of token to deposit.
* @param tag Newly generated TXO's y-axis value.
* @param a deposit proof data.
* @param b deposit proof data.
* @param c deposit proof data.
*/
function depositToMagicalWorld(
address erc20,
uint tag,
uint amount,
uint[2] memory a,
uint[2][2] memory b,
uint[2] memory c
) public {
ERC20Pool storage pool = pools[erc20];
require(pool.tags[tag] == Tag.Unspent, "TXO already exists");
// Check Deposit TXO's value is same with the given amount
require(
zkDeposit.verifyTx(
a,
b,
c,
[tag, amount, 1]
), "Deposit ZKP fails"
);
// Transfer ERC20 token. It should have enough allowance
IERC20(erc20).transferFrom(msg.sender, address(this), amount);
// Record the TXO as valid
pool.coinbases[tag] = true;
}
Building send request
Alice wants to send some amount of ERC20 tokens to Bob. Here we assume that Alice is managing the MMR tree herself because all of the data is available from the chain.
[Python sample code]
from py934.mimblewimble import TxSend, Output, Field, Request
from py934.mmr import PedersenMMR
...
tx_send = TxSend.builder(). \
value(1000). \
fee(100). \
input_txo(input_txo, inclusion_proof). \
change_txo(change_txo). \
metadata(erc20_address, expiration). \
sig_salt(sig_salt). \
build()
serialized = tx_send.request.serialize()
A Mimblewimble transaction can consume multiple input TXOs, but Ethereum 9¾ allows only to use up to 2 TXOs. Also, to verify the validity of the input TXO, it should have an inclusion proof except when the TXO is a coin-base. Exchanging this data using the Whisper protocol may help keep the anonymity.
We can decrease the call data size by about 20% by allowing only 1 TXO for the Mimblewimble input.
Responding to the send request
Bob receives the message, and the message from the sender looks like below:
[Python sample code]
>>> mw_request = Request.deserialize(serialized)
>>> print(mw_request)
val: 1000
fee: 10
public_sign: (19321..., 32190...)
public_excess: (39011..., 80173...)
metadata: 391238123910...
As above the printed result, Bob only knows about how much value he receives, the fee, metadata, and homomorphically hidden values of the sender’s signature and transactions excess. With this information, to accept the request, Bob makes a response like below:
[Python sample code]
txo = Output.new(1000)
...
tx_receive = TxReceive.builder(). \
request(mw_request). \
output_txo(txo). \
sig_salt(sig_salt). \
build()
serialized_response = tx_receive.response.serialize()
Constructing a zk-Mimblewimble transaction
As Bob answers the request, Alice now can merge the response and construct a valid Mimblewimble transaction. However, Alice wants to hide the input TXOs and replace them with spent tags. Thus, Alice also generates a proof to guarantee that the transaction which is hiding input TXOs still follows the Mimblewimble protocol. The merge function below proceeds these steps and constructs a zk-Mimblewimble transaction inside the function.
[Python sample code]
tx = tx_send.merge(tx_receive.response)
During the construction, it generates a proof against the following zk-SNARKs circuit to verify the Mimblewimble protocol.
[zk-SNARKs circuit in ./circuits/zkMimblewimble.code]
def main(\
field fee, field metadata, field[2] tags, field[2] outputTXO, field[2] changeTXO, field[2] sigPoint, \
private field[2] excess, private field[2] sigScalar, private field[2] inputRandoms, private field[2] inputValues \
) -> (field):
// Retrieve constants
RANGE = RANGE()
G = G()
H = H()
// Get transaction hash
field e = challenge(excess[1], sigPoint[1], fee, metadata)
// Check Schnorr sigScalar
1 == schnorr(sigScalar, sigPoint, e, excess)
// Fee should be less than 2^52
1 == lessThan(fee, RANGE)
1 == lessThan(inputValues[0], RANGE)
1 == lessThan(inputValues[1], RANGE)
// Get input TXO from r,v
field totalRandom = 0
field totalValue = 0
// Prove that the spentTag is derived from the inputKey
tags[0] == if tags[0] == 1 then 1 else spentTag(inputRandoms[0], inputValues[0]) fi
tags[1] == if tags[1] == 1 then 1 else spentTag(inputRandoms[1], inputValues[1]) fi
// Aggregate 2 TXOs
field[2] inputTXO1 = ecAdd(ecMul(inputRandoms[0], G), ecMul(inputValues[0], H))
field[2] inputTXO2 = ecAdd(ecMul(inputRandoms[1], G), ecMul(inputValues[1], H))
field[2] inputTXO = ecAdd(inputTXO1, inputTXO2)
// Secure that this transaction follows the Mimblewimble protocol
ecAdd(inputTXO, excess) == ecAdd(ecAdd(outputTXO, changeTXO), ecMul(fee, H()))
return 1
Roll up
The last step to finish the transaction is submitting it to Ethereum 9¾. It needs a new root and zk proof for the roll-up.
Make roll up proof
Computing a roll-up proof only needs the previous root and peaks, appended items, and the new root.
[Python sample code]
roll_up_proof_1 = PedersenMMR.zk_roll_up_proof(
root_0,
width_0,
peaks_0,
[output_txo_1_1.hh, output_txo_1_2.hh, output_txo_2_1.hh, output_txo_2_2.hh],
root_1
)
Submit roll-up to the contract
Then, Ethereum 9¾ contract’s roll-up functions require the ERC20 token address, previous root and new root of the roll-up, zk-Mimblewimble transactions, and the roll-up proof for its parameters. The roll-up functions execute the following actions:
- Collect fees from aggregated transactions.
- Verify that each transaction follows Mimblewimble protocol.
- checks range proofs, inclusion proofs, and Mimblewimble proof
- checks expiration
- Verify roll-up proof.
- Update root.
[Solidity code in ./contracts/Ethereum934.sol]
function rollUp2Mimblewimble(
address erc20,
uint root,
uint newRoot,
uint[52][2] memory mwTxs,
uint[8] memory rollUpProof
) public {
ERC20Pool storage pool = pools[erc20];
uint fee = 0;
uint[2][4] memory items;
for (uint8 i = 0; i < 2; i++) {
MimblewimbleTx memory mwTx = toMimblewimbleTx(mwTxs[i]);
require(verifyMimblewimbleTx(erc20, pool, mwTx), "Mimblewimble proof fails");
fee += mwTx.fee;
items[2 * i + 0] = [mwTx.output1.x, mwTx.output1.y];
items[2 * i + 1] = [mwTx.output2.x, mwTx.output2.y];
emit Mimblewimble(erc20, mwTx.output1.y);
emit Mimblewimble(erc20, mwTx.output2.y);
}
// Check roll up
require(
zkRollUp4.verifyTx(
[rollUpProof[0], rollUpProof[1]],
[[rollUpProof[2], rollUpProof[3]], [rollUpProof[4], rollUpProof[5]]],
[rollUpProof[6], rollUpProof[7]],
[root, pool.mmrWidths[root],
items[0][0], items[1][0], items[2][0], items[3][0],
items[0][1], items[1][1], items[2][1], items[3][1],
newRoot, 1]
),
"Roll up fails"
);
// Update root & width
require(root == 1 || pool.mmrRoots[root], "Root does not exist");
pool.mmrRoots[newRoot] = true;
require(pool.mmrWidths[root] + 4 < 66536, "This 16 bit MMR only contains 66535 items");
pool.mmrWidths[newRoot] = pool.mmrWidths[root] + 4;
delete pool.mmrRoots[root];
delete pool.mmrWidths[root];
IERC20(erc20).transfer(msg.sender, fee);
emit RollUp(erc20, root, newRoot, 2);
}
Deterministic fraud proof of the optimistic roll-up
Rolling up transactions consumes pretty much gas because of the zk-SNARKs computations. Therefore, skipping the computation cuts off the costs a lot. Thus the optimistic roll-up achieves 147k gas per transaction while rolling up 2 Mimblewimble transactions consumes about 7M gas.
Let’s take a look how the optimistic roll-up for Ethereum 9¾ works:
-
Original roll up
- Relayer submits roll up data.
- Contract verifies the zk-SNARKs proofs.
- Update the root & spent tags
-
Optimistic roll up
- Relayer submits roll up data.
- Contract records the hash value of the message data instead of compute them.
- For a given period, anyone can submit fraud proof. The important thing is that data for fraud proof is always available because all data are already submitted once to the chain. Once the fraud proof is submitted, it computes the zk-SNARKs verification and slash the submitter or not.
- If there is no valid fraud-proof for the given time, it finalizes the roll-up and updates the root and spent tags.
[Solidity code in ./contracts/Ethereum934.sol]
function optimisticRollUpMimblewimble(
address erc20,
uint root,
uint newRoot,
uint[52][] memory mwTxs,
uint[8] memory rollUpProof
) public {
uint qty = mwTxs.length;
require(qty == 4 || qty == 8 || qty == 16 || qty == 32, "Unsupported scale");
ERC20Pool storage pool = pools[erc20];
bytes32 id = keccak256(msg.data);
uint16 newWidth = pool.mmrWidths[root] + uint16(mwTxs.length * 2);
require(newWidth < 66536, "This 16 bit MMR only contains 66535 items");
uint fee = 0;
uint[] memory tags = new uint[](qty);
for (uint8 i = 0; i < qty; i++) {
fee += mwTxs[i][0];
tags[i] = mwTxs[i][2];
require(pool.tags[tags[i]] == Tag.Unspent, "Not a valid tag.");
pool.tags[tags[i]] = Tag.Spending;
}
RollUpObj memory rollUp = RollUpObj(
erc20,
msg.sender,
fee,
root,
newRoot,
newWidth,
now,
tags,
true
);
optimisticRollUps[id] = rollUp;
emit OptimisticRollUp(id, erc20, root, newRoot, qty);
}
Performance (without EIP 1108 & EIP 2028)
Call data size & TPS
The current implementation’s call data size is about 1.6 kB per transaction (52 * 32 bytes). If we do not allow to spend 2 input TXOs for a transaction, then the call data size decreases to 1.3 kB(42 * 32bytes).
struct MimblewimbleTx {
uint fee; // (32 bytes)
uint metadata; // (32 bytes) erc20 address & expiration
uint tag1; // (32 bytes)
uint root1; // (32 bytes)
Proof inclusionProof1; // (256 bytes)
uint tag2; // (32 bytes)
uint root2; // (32 bytes)
Proof inclusionProof2; // (256 bytes)
EllipticPoint output1; // (64 bytes)
Proof rangeProof1; // (256 bytes)
EllipticPoint output2; // (64 bytes)
Proof rangeProof2; // (256 bytes)
EllipticPoint sigPoint; // (64 bytes)
Proof txProof; // (256 bytes)
}
*It is going to see dramatic, approximately fivefold increase in TPS in Istanbul.
| Gas(Avg) | Gas per tx | Maximum TPS | |
|---|---|---|---|
| Roll up 1 tx | 3,859,179 | 3,859,179 | 0.17 tx / sec |
| Roll up 2 tx | 6,645,227 | 3,322,613 | 0.20 tx / sec |
| Optimistic roll up 16 tx | 2,492,927 | 155,807 | 4.25 tx / sec |
| Optimistic roll up 32 tx | 4,694,516 | 146,703 | 4.53 tx / sec |
Circuit performance
Test machine: Ryzen1700 (3GHz 8 Core) + DDR4 32Gb
| Circuits | Constraint points | Gas consumption | Proof generation time |
|---|---|---|---|
| Deposit proof | 29,140 | 612,273 | 3 seconds |
| Withdraw proof | 588,910 | 658,043 | 3.5 seconds |
| Range proof | 19,679 | 568,232 | 2 seconds |
| MMR Inclusion Proof | 399,644 | 613,809 | 24 seconds |
| Mimblewimble Proof | 141,552 | 975,399 | 9 seconds |
| MMR Roll up 2 items (1 txs) | 644,957 | 1,392,269 | 1m 47s |
| MMR Roll up 4 items (2 txs) | 968,099 | 1,392,269 | 1m 47s |
| MMR Roll up 8 items (4 txs) | 1,614,383 | 1,392,269 | 1m 47s |
| MMR Roll up 16 items (8 txs) | 2,906,951 | 2,127,267 | 3m 19s |
| MMR Roll up 32 items (16 txs) | 5,492,087 | 3,597,531 | 7m 20s |
| MMR Roll up 64 items (32 txs) | 10,662,359 | 6,541,946 | 17m 30s |
Conclusion
Mimblewimble secures private transactions between two parties with a lightweight computation, and the commitment-nullifier scheme completes the privacy by severing the links between inflow and outflow. Moreover, Pedersen MMR enhances the roll-up performance achieving 10M constraints to roll up 64 items using 16-bit Merkle Mountain Range.
As a result, because the relayers can aggregate transactions and gather some fee, it is expected to see appearance of new DAO systems. For example, we can build a system where everyone can participate as relayers and decide their transaction fee or delegate stakes for the optimistic roll-up to receive a share of the fee revenue. De-Fi products can also use this model for their investment sources.
Although the gas cost of the current implementation is affordable, when you consider that it secures the privacy, it becomes more expensive than a roll-up without Mimblewimble. Accordingly, the next step should be finding a way of reducing call data size and constraints as possible as we can. However, Ethereum 9¾ is still promising, and the upcoming Istanbul test is going to make it more affordable than a bare ERC20 transaction, even it is a private transaction. Therefore, the hope is to see a new daily-use ERC20 wallet that supports private transactions using Ethereum 9¾.
Future works
- Auditing and gas optimization.
- Version for the Istanbul fork.
- Mobile version of the proof generator.
- Integrating with clients like Status.
- Goblin’s network (optimistic roll-up in relayer’s network).
References
- Tom Elvis Jedusor. Mimblewimble whitepaper. MimbleWimble Origin · mimblewimble/docs Wiki · GitHub
- Andrew Poelstra. Mimblewimble precise paper. https://download.wpsoftware.net/bitcoin/wizardry/mimblewimble.pdf
- Vitalik Buterin. On-chain scaling to potentially ~500 tx/sec through mass tx validation. On-chain scaling to potentially ~500 tx/sec through mass tx validation
- What are zk-SNARKs. What are zk-SNARKs? - Z.Cash
- Karl Floersch. Ethereum Smart Contracts in L2: Optimistic Rollup. https://medium.com/plasma-group/ethereum-smart-contracts-in-l2-optimistic-rollup-2c1cef2ec537
- Ignotus Peverell and 25 contributors. Introduction to Mimblewimble and Grin. grin/doc/intro.md at f86eb18a6e3a10ecb96497f0d2be91fb231e7520 · mimblewimble/grin · GitHub
- Brandon Arvanaghi. Grin Transactions Explained, Step-by-Step. https://medium.com/@brandonarvanaghi/grin-transactions-explained-step-by-step-fdceb905a853
- 135 contriburos. Grin implementation. GitHub - mimblewimble/grin: Minimal implementation of the Mimblewimble protocol.
- Peter Todd. Merkle Mountain Range. opentimestamps-server/doc/merkle-mountain-range.md at ac35729035c84516bfd195d8463cd0419f901f37 · opentimestamps/opentimestamps-server · GitHub
- Ignotus Peverell and 4 contributors. Merkle Mountain Ranges. grin/doc/mmr.md at f86eb18a6e3a10ecb96497f0d2be91fb231e7520 · mimblewimble/grin · GitHub
- GitHub - barryWhiteHat/baby_jubjub_ecc: altbn128 twisted ewards curve point addion, point multiplicaion, eddsa signature verificaion and pedersen commiments
- GitHub - barryWhiteHat/roll_up: scale ethereum with snarks
- Zooko Wilcox. [Sapling] specify Pedersen hashes for a collision-resistant hash function inside the SNARK. [Sapling] specify Pedersen hashes for a collision-resistant hash function inside the SNARK · Issue #2234 · zcash/zcash · GitHub
- https://zokrates.github.io/