EthStorage: Scaling Ethereum Storage via L2 and DA

[qizhou]

Motivation

Reusing Ethereum mainnet security and extending Ethereum scalability are the major goals of Ethereum L2 solutions. Most existing L2 solutions such as rollups focus on scaling Ethereum computation power, a.k.a., higher transactions per second. Meanwhile, with the popularity of dApps such as NFT/DeFi/etc, the demand for storing a large amount of data reusing Ethereum mainnet security has grown dramatically.

For example, one strong storage demand comes from on-chain NFTs, where not only the token of an NFT contract is owned by the users, but also the on-chain images belong to the users. In contrast, storing the images on a 3rd party (e.g., ipfs or centralized servers) introduces additional trust, which can be easily and frequently broken (e.g., a lot of images of old NFT projects using ipfs are now unavailable).

Another demand is the front end of dApps, which are mostly hosted by centralized servers (with DNS). This means that the websites can be easily censored (happening for Tornado Cash). Further issues include DNS hijacking, website hacking, or server crash.

By reusing Ethereum mainnet security, all the aforementioned problems can be immediately solved. However, if everything is stored on-chain, the cost will be extremely high - for example, storing 1GB data using SSTORE will cost 1GB / 32 (per SSTORE) * 20000 (gas per SSTORE) * 10e9 (gas price) / 1e18 (Gwei to ETH) * 1500 (ETH price) = $10M! The cost can be reduced to 1/3x using a contract code, but it is still far more expensive than other storage solutions (S3/FILECOIN/AR/etc).

Goals

With L2 and data availability technologies, we believe that we can achieve an Ethereum storage scaling solution with the following goals:

• Increase the capacity to PB or more assuming that each node has a few TB disks
• Reduce the storage cost to 1/100x or 1/1000x vs SSTORE
• Similar KV CRUD semantics as SSTORE (a few limitations will apply, see below)
• Reuse Ethereum mainnet security on block re-organization, storage cost settlement, and censorship-resistant

Solution

How? The current cost of storing a large amount of data on the Ethereum mainnet comes in two parts

• Upload cost (calldata)
• Storage cost (SSTORE)

For the upload cost, with DA, especially danksharding, we are expecting the upload cost will dramatically be decreased in a near future - e.g., the current draft of EIP-4844 will have 1 gas per byte (i.e., ~128KB per BLOB given a BLOB size is ~128KB) and minimal gas price to be 1. The throughput of uploading can be further increased to ~10x by danksharding, which should further reduce the cost of uploading data.

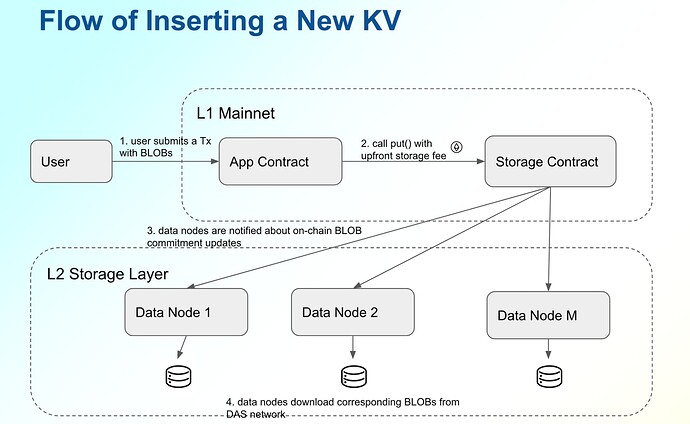
For the storage cost, our solution is to build a permissionless L2 data retention network. The L2 network contains the following components

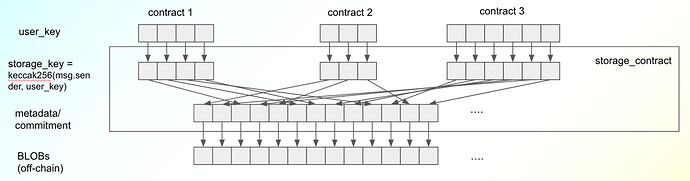
• a storage contract deployed on Ethereum mainnet, which offers KV CURD semantics such as put()/get()*/delete() besides verify(). The storage contract does not store the full values of the keys - only commitments (e.g., KZG commitment of BLOBs) are stored, while the corresponding data is available thanks to DA. The storage contract will also accept proof of storage and efficiently verify that data is stored in the data nodes in an L2 data retention network. (get()* is only available in data nodes, see below)
• data nodes run a special client of Ethereum (a modified version of geth and a consensus client), which synchronizes the latest state of Ethereum (and thus all commitments of the values of KV pairs). Further, the data nodes serve additional functions as
  • accept the configuration of which parts (i.e., shards) of BLOBs will host
  • synchronize the BLOBs of interest by joining the L2 data retention network
  • copy the BLOBs from the Ethereum mainnet DA network if the corresponding commitments in the storage contract are updated/appended in the storage contract
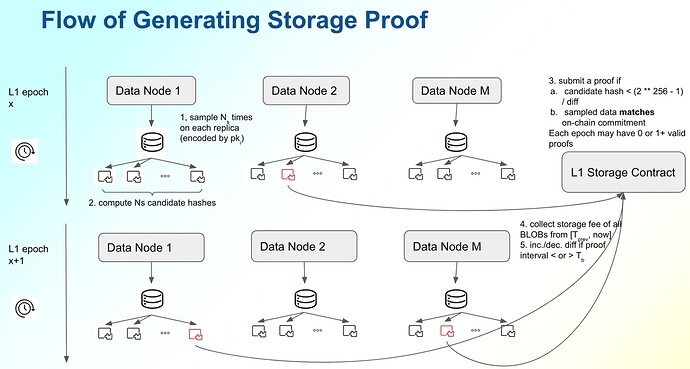
  • generate proof of storage, submit it to Ethereum mainnet, and collect storage fee
  • serve storage_contract.put() in JSON-RPC eth_call() method

Note that running a data node is completely permissionless - as long as a data provider has sufficient disk space, it could run a node, synchronize the BLOBs from L2 network, copy the BLOBs from DA if the commitments on L1 change, and prove the retention to L1.

Benefits vs Existing Solutions

Besides reusing Ethereum mainnet security, EthStorage can offer the additional benefits:

• Rich storage semantics (KV CRUD). FILECOIN/AR mostly works for static files, which lack efficient update/delete operations - i.e., the users have to pay twice to update existing data. Thanks to DA and smart contracts, EthStorage can offer full KV CRUD semantics similar to SSTORE.
• Programmability. The storage can be programmable by smart contracts, which can easily enable new features easily such as multi-user access control or data composability.
• Atomicity with application logic and storage logic. Current dweb using ENS generally requires two steps: 1, uploading the data to an external storage network; 2, storing the contenthash on ENS. With DA and EVM, EthStoage can complete both application logic and storage logic in a single transaction, which is more friendly to users (also widely found in Web2 applications, e.g., Twitter/FB/etc).
• Zero-onboarding cost. EthStorage is built on top of Ethereum, the storage cost is also paid by ETH, and thus, the storage operations can be done just by ETH wallet like Metamask - users do not have to learn new token/wallet/address.

Key Problems to Solve

• Proof of storage on large dynamic datasets with data redundancy: Enabling data redundancy in a decentralized way is a key challenge, especially the dataset changes constantly.
• Efficient recurrent storage payment: Submitting a valid proof of storage on-chain will reward the prover (or data providers) with a storage fee (in ETH). We need an efficient storage rental/payment model to ensure sufficient redundancy of the storage data perpetually.
• Rarity data discovery and token incentive to encourage auto re-replication: When some of the data nodes are off, we need to encourage other nodes to join the data retention network and replicate the data
• Efficient verification on-chain: We will explore some techniques, especially zero-knowledge proof to reduce the cost of verification.

Other Questions

• Q: What is the difference with DA?
  A: Current Ethereum DA is expected to expire the data in a few weeks or months (See Proto-Danksharding FAQ). EthStorage is expected to store the data permanently given some well-known assumptions on storage cost (e.g., storage cost over ETH price constantly drops every year). Further, EthStorage offers full KV CRUD semantics on-chain (note that read is limited to only data nodes).

• Q: What is the access protocol to read the storage EthStorage (similar to ipfs://)?
  A: The data can be retrieved by calling eth_call on a data node, which will search and retrieve the corresponding BLOBs in L2 network. Further, from an end-user perspective, we could use web:// access protocol to browse the BLOBs hosted by a smart contract, whose content can be dynamic.

[asn]

Hello Qi,

I think that your proposal can produce a useful system indeed.

That said, I don’t see an analysis of the issues with it. I would be curious to learn what you consider future roadblocks here, or items for future research.

For one, I know that Filecoin has trouble serving hot-storage items. IIUC this is partially because its SNARKs are quite expensive. On this note, I don’t see an analysis of plausible proof techniques, their performance, and how each of them impacts the hot storage capabilities of the system. Such a system needs strong confidence that the data exists and can be served back in time. An analysis of this part of the design would be useful.

Cheers!

[lydia]

Thanks Qi, this is really interesting. I like that you’re exploring different pricing models rather than going with a permanent storage model (which is plaguing the L1).

Seems to me that this can be a helpful tradeoff - I essentially can pay less but have less redundancy of my data. Maybe there are 100 replicas of my data instead of 400K on L1. Not unlike sharding but for only the storage resource. This seems reasonable given it’s probably a 1/n honest trust assumption.

A couple of questions

1. Do you expect the new price of storage to be roughly replica count / L1 validator count? Or do the savings scale more than just with the number of replicas?
2. As a full node, how do I validate the state posted to the L1 by the L2? If I don’t store the data myself, seems like I have to trust someone. I suppose they can gossip witnesses but I’m not able to validate every transaction unilaterally
3. How do you view the tradeoffs between this approach and the weak stateless model? If we end up with a centralized handful of block builders, do we still gain much scalability?

[qizhou]

@asn

For one, I know that Filecoin has trouble serving hot-storage items. IIUC this is partially because its SNARKs are quite expensive. On this note, I don’t see an analysis of plausible proof techniques, their performance, and how each of them impacts the hot storage capabilities of the system. Such a system needs strong confidence that the data exists and can be served back in time. An analysis of this part of the design would be useful.

Many thanks for your comments, George! Indeed, the problem of proving the storage on a large dynamic dataset with sufficient redundancy in the network (e.g., 30~50 replicas) on smart contracts is the probably most challenging problem here. The current solution of EthStorage is inspired by both proof of replications from FILCOIN and proof of random access from AR.

To prove the exact replications of the data, i.e., to prove n physical replicas of the data in the network, the basic idea of FILECOIN will ask each data provider to store a sealed version of raw data as

D_i = seal(D, pk_i)

where D is the raw data, pk_i is the key of the i th data provider, and D_i is the sealed replica. The sealing procedure is very time-consuming, taking about 6 hours on a high-performance machine for 32GB of data. Then, a time-limited interactive random challenge is performed so that pretending to store multiple physical replicas by computing the replicas with raw data on demand is impossible.

In the EthStorage case, we cannot use the FILECOIN solution directly since the raw data changes constantly. Instead, we use the idea of approximate proof of replication. First, for each BLOB stored in the network, we will ask to store the physical replica as

D_i^{(j)} = D^{(j)} \oplus mask(j, commitment(D^{(j)}), pk_i)

where D^{(j)} is the j th 128KB BLOB (with zero padding), and mask() is an electric-power expensive function, e.g., multiple rounds of Ethash, but can be computed in sub-seconds (so that we could update physical replica in a timely matter).

Now, for each Ethereum epoch (32 * 12 = 384s), given a random seed from prevRANDAO, we will ask each data provider to perform a large random sampling N_s, with each sampling corresponding to a hash candidate (like PoW). If a hash candidate satisfies the difficulty d (in the storage contract), then a valid proof of storage is found and the data provider can submit the proof to the Ethereum mainnet and collect the storage rental fee. The difficulty parameter will be adjusted on-chain similarly to Ethash difficulty adjustment algorithm but with a much larger expected submission interval T_b, which can be a couple of hours.

A couple of further comments on the idea:

• Given difficulty d, we could estimate the number of physical replicas as d / T_b / N_s
• The parameters such as N_s, mask function mask() should be chosen such that the cost of physical storage (including power cost + storage device lifetime cost) is much lower than the cost of computation on demand (i.e., raw data storage cost + computing mask() on demand + computation device lifetime cost). I have a simple calculator using typical Ethash mining data.
• Further, the mask() function should be easily and efficiently verified on-chain using ZKP. This area is open to research, and the current plan is to use a modified Ethash with Posiden hash to generate the initial DAG.
• A further extension can allow the data provider to store a part of all BLOBs, i.e., some shards of the BLOBs. This can be done by partitioning all BLOBs into non-overlapping shards (e.g., 4TB or 8TB size so that a commodity can store at least one) with each sharding having independent mining parameters (difficulty, prevhash, prev_submission_time, etc) in the storage contract.

I am happy to know if you have further questions or suggestions

[qizhou]

Hi Lydia, many thanks for your questions. Please see below for my answers.

@lydia

Do you expect the new price of storage to be roughly replica count / L1 validator count? Or do the savings scale more than just with the number of replicas?

I would expect the new price of storage will not depend on L1 validator count but depend on gas price and replica count. The EthStorage costs on Ethereum mainnet mainly consist of two parts: 1, put() method of storage contract to store a BLOB commitment and other metadata; and 2, mine() method of verifying proof of storage on-chain.

For put() method, it should be only charged based on the gas price * constant gas per metadata of a BLOB (commitment, kvIdx, etc) + a continuously-discounted upfront storage cost, where the upfront storage cost is a pre-setup parameter to ensure an expected number of replicas (with some assumption of profit margin, storage lifetime/power cost, etc)

For the proof of storage verification cost, the amortized cost of verifying the storage of each BLOB should be very small considering the proof is succinct thanks to ZKP and infrequent (average proof submission interval is targeted to be a couple of hours)

@lydia

As a full node, how do I validate the state posted to the L1 by the L2? If I don’t store the data myself, seems like I have to trust someone. I suppose they can gossip witnesses but I’m not able to validate every transaction unilaterally

Yes, that is the goal of the proof of storage part (see my above response to George’s question), where the network can show the proof on-chain that the data has been replicated with expected physical replicas. Further, such physical replicas must match the latest BLOBs that are posted on L1 (since we have all commitments of all BLOBs). Note that the availability of storage data is 1/N honest assumption, so we could safely trust on-chain storage proof as long as the proof can tell that there are sufficient replicas in the network.

@lydia

How do you view the tradeoffs between this approach and the weak stateless model? If we end up with a centralized handful of block builders, do we still gain much scalability?

This is a very good question, especially with the development of verkle tree in the Ethereum roadmap that we are closely watching. Note that one goal of EthStorage is to support ~PB capacity assuming each data node/provider can permissionless join the storage network with a few TB (4TB or 8TB for the current design). Further, if we can relax the CRUD semantics (e.g., put() and remove() with additional proof) so that we only maintain a single commitment on-chain for all BLOBs (instead of each commitment for each BLOB), the capacity should be theoretically unlimited (or limited by ETH supply). This may form a more decentralized storage network vs a centralized handful of block builders, where each may need PB capacity to generate verkle tree witnesses.

Hope this can answer your questions. Feel free to let me know if you have more

[qizhou]

I have received some questions raised by Dankrad, and the following are my responses:

Q1: The post sometimes seems to mix up data availability and storage. This is very concerning and to support any project in this domain we need to be sure that the builders are absolutely clear on the differences.

Many thanks for the question. The storage solution is built on top of Ethereum’s data availability, especially danksharding. From our understanding, Ethereum DA achieves two key goals:

1. Dramatically reduce the data upload cost (vs calldata) by running a DAS network of BLOBs, whose commitments are accessible by EVM;

2. Run a proof of custodian protocol to ensure that the DA BLOBs will be available to any other nodes for about 1 month.

Thanks to these key features of DA, EthStorage aims to achieve the following different goals using smart contracts and an L2 storage network:

1. (CRUD Semantics) Provide a CRUD KV store interface by an L1 storage contract such as put(key, blob_commitment), remove(key), get(key).

   a. An application (an EOA or contract) can create or replace a KV pair with put() method and remove a KV pair with remove() method in an Ethereum Tx. Upon calling put() method, the Tx would contain the values in the Tx’s BLOBs along with an upfront storage fee (in ETH). Note that the storage contract only maintains the mapping from key to value-commitment and incentives the nodes in L2 network to store the full values (i.e., BLOBs) off-chain. (Below graph illustrates a flow of inserting a new KV)
   

   

   b. For get() method, since EVM cannot directly read BLOBs from our storage network, get() method on EVM will fail with error: get() must be called in data nodes, while a data node (a special version of Eth node) can serve the get() method in a customized eth_call_with_blobs JSON-RPC.

2. (Proof of Storage with Desired Replicas) All KV pairs put from all applications are indexed and ordered from [0, 1, …, n-1] in the storage contract (see the below graph) depending on the insertion order. The ordered KV pairs will help our proof of storage system (based on random sampling) to prove that the BLOBs are stored in the EthStorage L2 network with desired physical replicas. Further, becoming a data provider and hosting a replica should be permissionless - anyone can download the latest BLOBs from the L1 DAS network, and synchronize the rest BLOBs from the L2 network (assuming at least one is honest). Once a node has the latest replica, it could efficiently generate the storage proof and submit the storage proof to collect the storage fee (please see more details in our response to Q4).

3. (Recurrent Storage Rental Model) Upon calling put() to create a new KV, an upfront storage fee (in ETH) will be transferred to the storage contract for permanent storage. Upon submitting a valid proof of storage, the storage fee will be distributed to the storage provider in a discounted payment flow model in perpetuity, assuming the storage cost in ETH/GB constantly decreases over time (see our response to Q4 for a detailed analysis).

Q2: To me there is insufficient clarity on how different this is from existing storage networks like IPFS, Arweave, Swarm etc.

Many thanks for the question. The following table summarizes the difference between existing storage networks including FILECOIN and Arweave:

	Filecoin	Arweave	Ethereum SSTORE/SLOAD	EthStorage
Store Object	Static Files	Static Files	KV Store	KV Store
Semantics	CRD	CR	CRUD	CRUD*
On-Chain Programmable	No	No	Yes	Yes
Proof of Storage	Proof of Space-Time with Challenge	Succinct Proof of Random Access	Fully Replicated	ZKProof of Random Access
Replication Guarantee	High	Median	Very High	High
Storage Cost	Very Low	Low	Very High	Low
Capacity	~ EB	~ 100 TB (Current)	~ 1 TB	~ PB
Access Protocol	ipfs://	N/A	web3://	web3://
Wallet	Filecoin Wallet	ArWallet	ETH-Compatible	ETH-Compatible

*Some limitations are applied, see below.

Q3: Some things in this proposal seem impossible to implement in my opinion, for example the ability to access this key-value store through a smart contract. I would like further clarity on how this can even be implemented.

Many thanks for the question. Admittedly, compared to SSTORE/SLOAD, the proposed storage layer has some limitations on full CRUD KV semantics, mainly for get(key) returns (bytes) method since EVM cannot access off-chain BLOBs directly. Serving get(key) method of the storage contract from another contract/EOA is only available in our customized eth_call_with_blobs JSON-RPC on a data node. When get(key) is called during an eth_call_with_blobs RPC, the data node will search/retrieve the BLOB of the key from the L2 storage network.

Note that put(key, blob_commitment) and remove(key) can be fully supported and called in an Ethereum Tx. However, if a Tx needs to read the value (e.g., get the value of a key, copy bytes from the range [20, 100], and put the value back), we have to pass the value (BLOB) as calldata, call storge_contract.verify(key, value), and then use the verified value to complete the rest of the Tx. This should be similar to the on-chain challenge of optimistic rollups, where the sequencer uploads L2-ordered Txs as L1 BLOBs, and a challenge Tx will use calldata to reveal the actual L2 Txs from DA.

Q4: It is also confusing to claim that this storage layer can have Ethereum mainnet security. I don’t think this is true unless we fundamentally change the way the protocol works as well.

Many thanks for the question. We agree that achieving the Ethereum mainnet security for the storage layer is a very challenging open research problem. To address the problem, we want to prove that the desired number m (m is decently large, 50 or 100) of physical replicas are stored in the network with 1/m honest assumption, i.e, at least one replica is available in the network. Further, such proof can be efficiently verified on-chain using ZKP.

Note that a similar 1/m assumption should hold for optimistic rollups, which require the L2 world state is available on at least one honest L2 node (since DA only has recent 1-month L2 blocks). Moreover, we require the m replicas are physically stored - as a comparison, in the proof of custody, multiple validators can share one physical replica to compute the bomb. In addition, although the current design requires all data providers to store a full replica of BLOBs, we can demonstrate that a smart-contracted-based data sharding scheme can be introduced so that every data provider with a minimum storage capacity (e.g., 4TB) can group together to form a permissionless storage network storing ~m replicas (vs. Validum which has a committee of trusted storage nodes, e.g., StarkWare’s StakeEx).

Now, the key questions may become

a. how to incentivize the data nodes to store m physical replicas?

b. how to ensure the m replicas are physically stored by data providers? Or a malicious data provider with one physical replica will be economically inefficient to fool the system that the provider has multiple replicas?

c. how to build the ZKP proof system?

Incentivization for Storing m Physical Replicas

For the incentivization for storing m physical replicas, we need to estimate the upfront storage fee for each 128KB BLOB and the payment schedule based on the aforementioned discounted storage payment/rental model.

For the amount of the upfront storage fee per 128KB BLOB, we could estimate it as follows. Suppose a 2TB SSD costs $200 with 5 years lifetime and a maximum power of 7.2W/h (from Samsung 980 Pro spec), and the electric price is $0.068 kW/h, then the storage cost of per 128KB BLOB for the first year in ETH (assume 1ETH=$1000) is

\frac{128KB}{2TB}\left(\frac{200}{5} + \frac{7.2 \times 24 \times 365 \times 0.068}{1000} \right) \frac{1}{1000} \approx 3Gwei

Suppose the profit margin for data providers is 50\%, m = 50 replicas, and the yearly discounted rate of ETH/TB is 5\%, then the storage contract will ask users to pay the upfront storage fee per BLOB (only at the first time calling put() with a non-existing key) as

3Gwei \times 1/50\%\times 50 \times 1/5\% = 6000 Gwei

Given the upfront storage fee per BLOB from the users, the payment amount to the data providers in a time interval (in seconds), i.e., the rental fee over a specific time window, can be efficiently calculated on-chain using the discount payment flow model (need to convert yearly discount rate to secondly, here the code). This can be easily extended to pay data providers that host multiple BLOBs as long as all BLOBs stick to the same storage fee model.

As a comparison, using SSTORE (storing 32 bytes with 20000 gas) with gas price = 10Gwei, storing 128KB data on-chain will cost

\frac{128KB}{32} \times 20000 \times 10Gwei = 0.8192 ETH

which implies that the cost saving is 0.8192e18 / 6000e9 = 136533 x.

Proof of Storing m Physical Replicas

To address the malicious data provider issue, we use a solution inspired by both proof of replications from FILCOIN and proof of random access from AR. First, let us formulate the problem as follows.

Problem 1 (Proof of Storage Problem): Given a list of BLOBs [D^{(0)}, D^{(1)}, … D^{(n-1)}], |D^{(j)}| \leq 128KB with commitments [c_0, c_1, … c_{n-1}] and a list of m \ge 1 private keys$[pk_0, pk_1, …, pk_{m-1}]$, design an encoding function

D_i^{(j)} = encode(j, D^{(j)}, pk_i)

and a verification procedure such that generating a proof passing the verification based on D_i^{(j)} ‘s is economically much cheaper than on-demanding computation on encode(j, D^{(j)}, pk_i).

The solution we are proposing chooses the encoding function as

D_i^{(j)} = pad(D^{(j)}) \oplus mask(j, c_j, addr_i)

where pad(.) is the zero-padding function such that |D^{(j)}_i| = 128KB, mask() is an electric-power expensive function, e.g., multiple rounds of Ethash, and addr_i is the address of pk_i.

Now, we run the following protocol on the L1 storage contract: for each Ethereum epoch (32 * 12 = 384s), given a random seed from prevRANDAO, the storage contract will allow each data provider with a private key pk_i to randomly sample D_i^{(j)} ’s up to N_s times (a fairly large value), with each sampling corresponding to a hash candidate (like PoW). If a hash candidate satisfies the difficulty d condition in the storage contract, then a valid proof of storage is found and the data provider can submit the proof to the Ethereum L1 and collect the storage rental fee of all BLOBs in the time interval since the last submission to now. For each submission, the difficulty parameter will be adjusted on-chain similarly to Ethash difficulty adjustment algorithm but with a much larger expected submission interval T_b (e.g., a couple of hours) so that the gas cost of submitting the proof in an L1 Tx can be amortized.

Cost Calculation Example

The following gives a quick calculation of the cost of producing a hash candidate via physical storage vs on-demand computation. Suppose the sample size is 64KB, 2x2TB SSD costs $400 with 5 years lifetime with maximum power 14.4W/h and read performance 2\times1,000,000 4K-IOPS (2x Samsung 980 Pro Spec), the electric price is $0.068 kW/h, and N_s = 4 \times 1024 \times 1024 = 4194304, then per hash candidate cost of physical storage will be

cost\_per\_year =\left(\frac{400}{5} + \frac{14.4 \times 24 \times 365 \times 0.068}{1000}\right) \approx \$88.58

cost\_per\_sec = \frac{cost\_per\_year}{365 \times 24 \times 3600} \approx \$2.8078\times10^{-6}

cost\_per\_candidate = \frac{cost\_per\_second}{\min(2000000 \times4K/64KB,N_s / 384)} \approx \$2.58 \times 10^{-10}

Now, suppose we use a 24-rounds of Ethash with 128-byte output, and use Nvidia 3080 GPU at $1000 with 12GB single-round Ethash throughput @ 240W/h (from whatomine.com given output size is 128 bytes), then the per hash candidate cost using on-demand computation becomes (Note that the storage cost is not included in the calculation)

\left(\frac{1000}{4} + \frac{240 \times 24 \times 365 \times 0.068}{1000}\right) \frac{64KB \times 24}{12GB/s} \approx \$1.52 \times 10^{-9}

As a result, using on-demand computation to fool the system will be 1.52 \times 10^{-9} / 2.58 \times 10^{-10} \approx 6 x times higher cost than storage. Moreover, the cost gap can be higher if the number of Ethash rounds increases. An example calculator can be found here.

Efficient On-Chain Verification Based on ZKP

Once a valid hash candidate is found, we need to verify that the sampled data D_i^{(j)} ’s matches the on-chain commitment c_j at randomly sampled positions of j. However, directly uploading samples and unmasking the data to original data D^{(j)} will be computationally prohibited on-chain. To verify the proof on-chain efficiently, we have to resort to a ZKP system.

This part is under heavy investigation, especially on how to build a ZKP on multi-round Ethash. We are exploring a couple of ZKP tools such as Circom/Halo2/etc and estimating the circuit size and proof time. The good thing is that the proof generation is not time-sensitive vs other ZK-based L2 - if the expected proof submission interval is a couple of hours, then generating a proof in a few minutes should be acceptable.