One way that the protocol can raise money to fund rewards (or possibly reduce the total ETH supply if that’s what we want) is by “reclaiming” a portion of transaction fees that are included in blocks.
What we cannot do is implement a simple percentage rule, eg. “20% of all txfees get burned”; the reason is that this creates incentives for miners to accept txfee payments via side channels (eg. literal payment channels, or some cryptocurrency with ultra-cheap txfees like dogecoin). What we can do is have a (monotonically nondecreasing) fee function f(g), where g is the amount of gas in a block and f(g) is the amount charged to miners, where f(g) depends on nothing except for the gas used itself. For example, f(g) = 5*10**9 * g would simply charge a flat fee of 5 gwei per gas. This would lead to no perverse incentives of the type described above, because the fee is charged based on the fact that the transaction is included, and not details about how it is paid for.
The question then is, how do we set f(g)? The main risk is that if we set it too high, then we accidentally deter transactions from being sent. Right now, for example, fees are around 1-20 gwei, but do we know that this will continue being the case in the future? Maybe future fees will drop to 0.01 gwei because the price of ETH rises massively without a corresponding uptick in blockchain transaction demand.
Here are two proposals:
f(g) = x * gfor an in-protocol maintained valuex, which gets updated like a control system: if blocks are more than half full,xgoes up, if blocks are less than half full,xgoes downf(g) = k1 * (2 ^ (g / k2) - 1)- for example, k1 = 100 gwei, k2 = 500,000, so marginal fee per gas is 0.00013 gwei for the first unit of gas, 0.00055 for the millionth, 0.14 for the 5 million-th, 9 gwei for the 8 million-th, 145 gwei for the 10 million-th
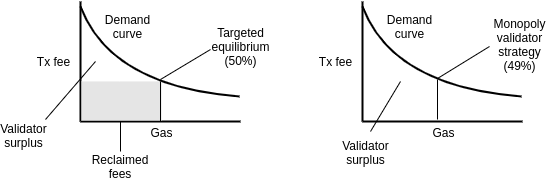
The first formula targets blocks in the long run always being half-full. Under “normal conditions”, it seems like it could quite possibly recapture a large portion of the value of txfees. However, if we assume a monopoly validator cartel, then the monopolist’s optimal strategy is to simply keep blocks 49% full, which would lead to the reclaimed fees dropping to zero.
Note that it’s also possible that the monopoly profit-maximizing gas per block is lower than 50%; in this case, the monopoly equilibrium will be lower, and the fee claiming scheme will not affect it at all.
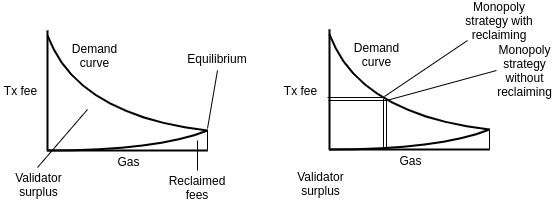
The second formula presents an exponential cost curve to the validators. The purpose of the curve being exponential is that the cost curve effectively substitutes the gas limit, and we want to make sure that the de-facto gas limit remains reasonable across a wide array of transaction fee cost conditions. The fees reclaimed are much smaller. In the case of a monopoly, the reclaimed revenue does not quite go to zero, but it still reduces greatly. The optimal quantity of gas for a monopolist to accept decreases because of the reclaiming mechanic, but only slightly.
There exists a third possibility: charge f(g) = x * g, but where x is determined based on an exponential function based on the gas in the previous block. In the normal case, this would be similar to the first left diagram, where the entire rectangle would be reclaimed. In the monopoly case, this would be similar to the second right diagram, as since the monopolist controls every block, basing x on the previous block and the current block is essentially the same policy. Hence, this third approach may be able to combine the benefits of the first two, providing both maximum fee reclaiming in the normal case, and still some degree of fee reclaiming in the monopoly case.
Note that this is all fairly non-rigorous in that it doesn’t look deeply at the incentives that cause transaction senders to change the fees that they offer based on what they observe, but hopefully it does serve as a good introduction to some of the issues at hand.