FHE-DKSAP: Fully Homomorphic Encryption based Dual Key Stealth Address Protocol

[Mason-Mind]

This research is a joint effort from Ethereum Fellows: @Mason-Mind @georgesheth @dennis @AshelyYan

1. Introduction

The Stealth Address (SA) prevents the public association of a blockchain transaction with the recipient’s wallet address. SA effectively conceals the actual destination address of the transaction. It is critical to protect privacy of recipients and cut off social engineering attack on transaction flow.

@vbuterin @Nero_eth proposed EIP-5564 as the first SA design, and developed BasedSAP as a implementation of SA on Ethereum by utilising the Secp256k1 elliptic curve (EC). However, @vbuterin also highlighted the current limitations in Open problem: improving stealth addresses to demand a (Fully Homomorphic Encryption) FHE solution:

@vbuterin

Another alternative is to use fully homomorphic encryption (FHE) to outsource checking: use FHE to allow some third party to walk through the entire set of encrypted values, decrypt each value, and return the values that decrypt correctly. Given FHE as a “black box protocol” this is conceptually simpler; it also means that complicated constructions to store and maintain data off-chain are not necessary. However, the FHE approach may be more expensive.

Based on BaseSAP, we contribute further to propose FHE-DKSAP: a SA protocol with Fully Homomorphic Encryption (FHE). FHE-DKSAP has bellow primary advantages:

• FHE-DKSAP replace EC with FHE to improve security level. FHE constructs the lattice cryptographic, and born to equip FHE-DKSAP to prevents quantum computing attacks.
• Therefore, SA in FHE-DKSAP is secured to be reused and no need to generate large amount of SA to reduce the complexity and difficulty of SA adoption.
• Comparing to the dual-key design in EIP-5564, our design in FHE-DKSAP, can help the receiver outsource the computation of checking the entire chain for SA containing assets without revealing his view key.

2. Background

One of the key focus of privacy protection in the Ethereum is to cut off the public association of the receipt’s address. SA is proposed to require the sender to create a random one-time address for every transaction on behalf of the recipient so that different payments are made to the same payee unlinkable.

We systematically studied on previous publications, and found Dual-Key Stealth Address Protocols (Courtois, N. T., & Mercer, R. 2017) is the most appreciated design. However, it is still vulnerable to key leakage attacks and quantum computing attacks. To prevent these attacks, we propose to implement SA with FHE, an application of lattices.

Others research can be summarised as bellow:

• The development of Stealth Address (SA) technology began with its initial invention by a user named ‘bytecoin’ in the Bitcoin forum on April 17, 2011. This technique introduced the concept of untraceable transactions capable of carrying secure messages, paving the way for enhanced privacy and security in blockchain systems.
• In 2013, Nicolas van Saberhagen took the concept further in the CryptoNote white paper, providing more insights and advancements in Stealth Address technology. His contribution expanded the understanding of how Stealth Addresses could be integrated into cryptographic protocols. Subsequent years saw several researchers making strides in the realm of Stealth Address technology.
• In 2017, Nicolas T. Courtois and Rebekah Mercer introduced the Robust Multi-Key Stealth Address, which enhanced the robustness and security of the SA technique.
• The year 2018 saw Fan Xinxin and his team presenting a faster dual-key Stealth Address protocol, specifically designed for blockchain-based Internet of Things (IoT) systems. Their protocol introduced an increasing counter, enabling quicker parsing and improving overall efficiency.
• In 2019, Fan Jia and his team tackled the issue of key length in Stealth Addresses by utilizing bilinear maps, thereby making significant advancements in enhancing the protocol’s security and practicality.
• The same year, researchers introduced a lattice-based linkable ring signature supporting Stealth Addresses. This innovation was aimed at countering adversarially-chosen-key attacks, further reinforcing the security aspect. However, this paper is not leveraging multi-keys.
• As technology progressed, EIP-5564 was proposed to implement SA on Ethereum and on June 25, 2023, the paper, BasedSAP emerged as a fully open and reusable Stealth Address protocol.

Based on our knowledge, all research did not resolve to meet overall requirements on 1) protect privacy on Ethereum, 2) prevent quantum computing attacks, 3) reuse SA rather than creating many.

3. Our Design: FHE-DKSAP

We resolve challenges by adopting FHE into DKSAP, and name our new design as FHE-DKSAP:

We present FHE-DKSAP with details as bellow. It requires preliminary knowledge on DKSAP and FHE, and you may read Chapter 6 first to have these knowledge ready:

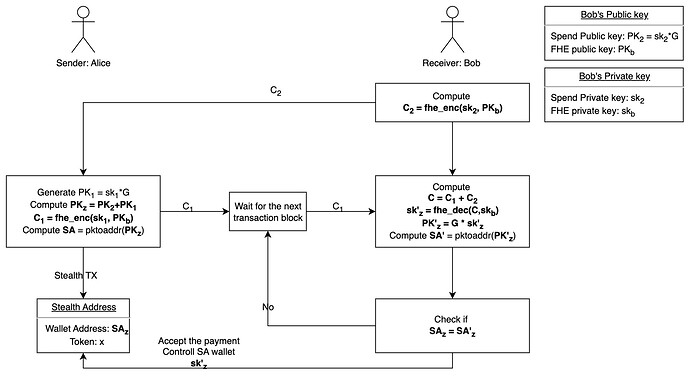
1. Bob (receiver) creates two key pairs: (sk_2, PK_2) and (sk_b, PK_b).
   1.1. sk_2 is a randomly generated Ethereum wallet private key for SA spending purpose. It does not need to register on Ethereum before use and is not Bob’s wallet private key.
   1.2. A SA spending wallet address public key PK_2 is generated using sk_2. It follows standard Ethereum address conversion from sk_2 to PK_2. As said, the final wallet address by PK_2 does not need to register on Ethereum before use.
   1.3. sk_b is the FHE private key for SA encryption and decryption.
   1.4. PK_b is used to encrypt the value of sk_2 to get the ciphertext C_2. Because FHE prevents quantum computing attacks, it is safe to encrypt sk_2 into C_2.
   1.5. Bob publicly shares PK_2, PK_b, and the ciphertext C_2.

2. Alice (sender) generates a key pair (sk_1, PK_1) randomly for each SA transaction.
   2.1. sk_1 is Ethereum ephemeral and the public key or wallet address does not need to register on Ethereum before use.
   2.2. She combines the two public keys for Ethereum wallet generation, PK_1 and PK_b, to obtain PK_z.
   2.3. The Stealth Address (SA) is generated based on PK_z by following standard Ethereum address conversion.
   2.4. Alice encrypts the secret key sk_1 using Bob’s FHE public key PK_b, resulting in the ciphertext C_1. Alice then broadcast C1, so that Bob is able to get it in an untrackable manner.
   2.5. Alice can not know SA’s private key, as nobody can guess private key from public key PK_z. It means Alice only knows where to send SA transaction, but never be able to login to this SA wallet.

3. Bob receives the ciphertext C_1 and adds two ciphertexts (C_1, C_2) together to get the C.
   3.1 With the additive homomorphism, he can decrypt the ciphertext C with his FHE private key sk_b. The FHE decryption result is the private key sk_z to the wallet that receives the sent from Alice.
   3.3. Then, he can generate the stealth address with sk_z and decrypt it with the private key, which only bob owns.So Bob is capable of transferring its balance with the private key sk_z for SA wallet .

Based BasedSAP, FHE-DKSAP has bellow improvement:

• It protects privacy of stealth address by computing over ciphertext.
• Compared to DKSAP and BasedSAP, our design remove the risk of leakages on keys and personal information.
• Meanwhile, it can prevent quantum computing attacks as well.

4. Our Implementation: FHE-DKSAP

We have implement FHE-DKSAP in Python and we will provide code here soon.

5. Our Evaluation: FHE-DKSAP

We have tested FHE-DKSAP and comparing to BaseSAP and we will provide evaluation here soon.

6. Other reading

6.1 Recap of Dual-key Stealth Address Protocol (DKSAP)

DKSAP builds on the Diffie-Hellman (DH) key exchange protocol in elliptic curve (EC). When a sender (A) would like to send a transaction to a receiver (B) in stealth mode, DKSAP works as follows:

Definitions:

• A “stealth meta-address” is a set of one or two public keys that can be used to compute a stealth address for a given recipient.

• A “spending key” is a private key that can be used to spend funds sent to a stealth address. A “spending public key” is the corresponding public key.

• A “viewing key” is a private key that can be used to determine if funds sent to a stealth address belong to the recipient who controls the corresponding spending key. A “viewing public key” is the corresponding public key.

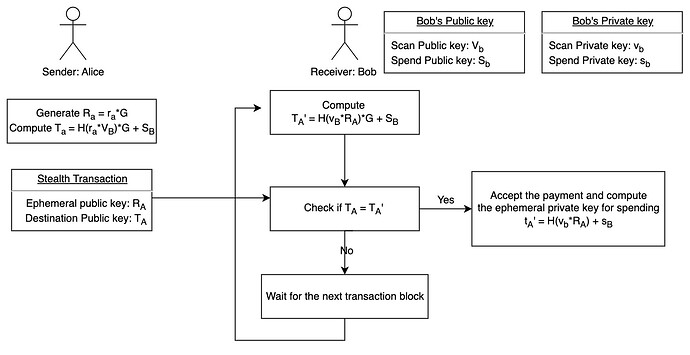
1. The receiver B has a pair of private/public keys (v_B, V_B) and (s_B, S_B), where v_B and s_B are called B’s ‘viewing private key’ and ‘spending private key’, respectively, whereas V_B = v_BG and S_B = s_BG are the corresponding public keys. Note that none of V_B and S_B ever appear in the blockchain and only the sender A and the receiver B know those keys.
2. The sender A generates an ephemeral key pair (r_A, R_A) with R_A = r_AG and 0 < r_A < n, and sends R_A to the receiver B.
3. Both the sender A and the receiver B can perform the ECDH protocol to compute a shared secret: c_{AB} = H(r_A*v_B G) = H(r_A*V_B) = H(v_B*R_A), where H(·) is a cryptographic hash function.
4. The sender A can now generate the destination address of the receiver B to which A should send the payment: T_A = c_{AB}G + S_B. Note that the one-time destination address TA is publicly visible and appears on the blockchain.
5. Depending on whether the wallet is encrypted, the receiver B can compute the same destination address in two different ways: T_A = c_{AB}G + S_B = (c_{AB} + s_B)G. The corresponding ephemeral private key is t_A = c_{AB} + s_B, which can only be computed by the receiver B, thereby enabling B to spend the payment received from A later on.

6.2 Fully Homomorphic Encryption

Homomorphic Encryption (HE) refers to a special type of encryption technique that allows computations to be done on encrypted data, without requiring access to a secret (decryption) key. The results of the computations remain encrypted, and can be revealed only by the owner of the secret key. There are additive homomorphism and multiplicative homomorphism as below:

Additive homomorphism: E(m_1) + E(m_2) = E(m_1+m_2)

Multiplicative homomorphism: E(m_1) * E(m_2) = E(m_1*m_2)

A homomorphic encryption scheme consists of four procedures, E = ( KeyGen, Encrypt, Decrypt, Evaluate):

• (sk, pk) ← KeyGen (1^λ, 1^τ ). Takes the security parameter λ and another parameter τ and outputs a secret/public key-pair.

• c ← Encrypt(pk, b). Given the public key and a plaintext bit, outputs a ciphertext.

• b ← Decrypt(sk, c). Given the secret key and a ciphertext, outputs a plaintext bit.

• c ← Evaluate(pk, Π, c ). Takes a public key pk, a circuit Π, a vector of ciphertexts, one for every input bit of Π, and outputs another vector of ciphertexts, one for every output bit of Π.

Currently, numerous fully homomorphic encryption (FHE) algorithms exist. Gentry was the pioneer in proposing a homomorphic encryption algorithm capable of performing both multiplication and addition operations. However, its practical implementation has been limited. Another significant advancement is the BGV scheme, which introduces a novel homomorphic encryption construction technology.

7. Conclusion

Motivated by the DKSAP and BaseSAP, we propose the FHE-DKSAP to help the receiver outsource the computation of checking the entire chain for stealth addresses containing assets without revealing his view key, and prevent quantum computing attacks.

[galadd]

@Mason-Mind

1.5. Bob publicly shares PK_2 PK2PK_2 , PK_b PKbPK_b , and the ciphertext C_2 C2C_2 .

Is there a reason why the ciphertext C_2 C2C_2 is publicly shared?

[Mason-Mind]

Good question @galadd. it is not necessary to publicly share the C_2 from the algorithm and computation point of view. But to allow any party to be able to calculate the homomorphois addition of C_1 and C_2 reduces the computation cost on Bob client’s side.

[changwu]

@Mason-Mind

2.2. She combines the two public keys for Ethereum wallet generation, PK_1 PK1PK_1 and PK_b PKbPK_b , to obtain PK_z PKzPK_z .

Thanks for sharing! I think PK_b here refers to PK_2.

[Mason-Mind]

Thanks for your feedback and you are correct. We have modified accordingly.

[NicLin]

This is very interesting! I have a few questions:

1. A dumb question as I’m not an expert on cryptography. Does it require FHE? As I see it only needs additive homomorphism during encryption/decryption?

2. You mentioned the SA can be reused though in step 2 Alice would generate a new key pair for each SA transaction. Can you elaborate more on the SA reuse part? Does the reuse mean reusing the same key pair for different SA transaction?

Thanks!

[Mason-Mind]

Thanks for proposing these two interesting questions.

1. Yes, you are right. This scheme only requires the additive homomorphism, however, we build this under FHE scheme such as BGV, BFV.
2. Bob’s key pairs can be reused (same key pairs), whereas Alice generates new key pairs for different SA transactions each time.

[Mason-Mind]

Here we attach our performance evaluation:

1. Motivation

To thoroughly assess the performance and effectiveness of FHE-DKSAP, we analyse SAP computation time and storage of the generated stealth addresses. Specifically, we evaluated the stealth address generation process using three different setups: DK-SAP (Plain), HE-DKSAP (Pallier), and FHE-DKSAP(Concrete). We found that FHE-DKSAP achieves advantage by striking a balance between computational complexity and efficiency, ensuring efficient processing while maintaining a secure and private transaction environment.

2. Environment setup:

Processor: Linux, 2.3 GHz Quad-Core Intel Core i5; Memory: 8 GB 2133 MHz LPDDR3

Python Version 3.9

Python-Paillier 1.2.2

Concrete: zamafhe/concrete-python:v2.0.0

3. Computation Time Benchmark:

	DK-SAP (Plain)	HE-DKSAP-Pallier	FHE-DKSAP-Concrete
Average 100 times (s)	0.019381137	0.445608739	0.035593492
Max (s)	0.022189946	0.98295696	0.050955667
Min (s)	0.017513547	0.108804308	0.028709731

We summarize as follows:

1. DK-SAP excels in computational speed due to its lack of privacy-preserving encryption.

2. HE-DKSAP-Paillier balances enhanced data privacy with longer computational time due to the intricate encryption and decryption of the Paillier scheme, which is around 20 times slower compared to the plain scheme.

3. FHE-DKSAP-Concrete is slightly slower than unencrypted DK-SAP but notably faster than HE-DKSAP-Paillier. This efficiency is thanks to its implementation in the RUST programming language, highlighting the importance of suitable tools for execution.

4. On-Chain Storage Benchmark:

DK-SAP Plain:

Information on chain	Bits	Example
PK_scan	160	(0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
PK_spent	160
R (public key of Alice)	160

HE-DKSAP-Paillier:

Information on chain	Bits	Example
PK_bob	160	(0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
PK_fhe_bob	128	192ace432e
C1	48	0x7faf7cf217c0

FHE-DKSAP-Concrete

Information on chain	Bits	Example
PK_bob	160	(0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
PK_fhe_bob	128	hi+SltsSwYnILVvNl5mFp+jbKJnlxwg7r7g1DGr8QQs=
C1	NA*	NA*

NA*: The outcomes are contingent upon the specific FHE schemes adopted by the Concrete library.

We can see both HE-DKSAP-Paillier and FHE-DKSAP-Concrete consume less storage than DK-SAP Plain.

5. Analysis

From our performance testing, we have identified the key advantages of FHE-DKSAP:

1. Protection Against Quantum Computing Attacks: It’s worth noting that FHE schemes like BGV, BFV, and CKKS are built upon learning with error assumptions, inherently fortifying our FHE-DKSAP against potential quantum computing attacks.

2. Key Reusability: The process of generating the Stealth Address (SA) hinges on the public keys of both parties involved. Yet, should Alice decide to alter her key pair, it results in a distinct SA. This, in turn, allows for the potential reusability of Bob’s key pair.

3. Optimized Computation Time: The off-chain computation of the stealth address using FHE-DPSAP proves to be acceptable in terms of computation time.

4. Minimal Storage Footprint: FHE-based DK-SAP demonstrates an advantage in terms of storage efficiency on the chain, which is considerably smaller than that of the plain DK-SAP method.

[maniou-T]

Great. It’s a valuable idea to solve privacy issues in blockchain transactions by hiding the recipient’s wallet address.

[stanislavkononiuk]

inputset = [(48915617476484211273115281063704461783033490425405257564258124598871191647089, 48915617476484211273115281063704461783033490425405257564258124598871191647089), (0x0, 0x0), (0x3350, 0x3350)]

You should regard first parameter ‘48915617476484211273115281063704461783033490425405257564258124598871191647089’ as string.
In generally, cipher branch, we should treat long integer as string.
Int type is 4 byte , maxim 8 byte, so can treat integer less than 2^8.
But OS support long number operation. As a software developer, we have to know of that.
If then you can do everything with this.
If you need anyhelp , let’s meet in upwork.
https://www.upwork.com/freelancers/~011c0baf85fae94170
It’s me.

[Mason-Mind]

Here are some listed resources that might be helpful for your code.

1. For wallet generation and smart contract creation, please consult Ethereum Improvement Proposal (EIP) 5564: EIP 5564 Documentation.
2. To learn more about the Paillier package, please refer to its documentation available here: Python Paillier Documentation.
3. For the implementation of Fully Homomorphic Encryption (FHE), you can find the relevant code on this GitHub repository: Zama AI - Concrete GitHub.

[randhindi]

Nice work! Is your implementation code available somewhere? Maybe our team can take a look and see if there are additional improvements we can make

[Mason-Mind]

Thanks for the reply @randhindi We already got in touch with your team during Token2049. We would like to collab on this:)