Futarchy with Bonding Curve Tokens

Applications
1

This post proposes a self-contained futarchy mechanism for bonding curve tokens.

Problem

Decentralized exchanges are likely the best price-finding solution for futarchy markets but, until they’ve achieved sufficient usability and liquidity, futarchies must be self contained providing their own price-finding mechanism. The current best know solution is to use an LMSR automated market maker but this presents a significant challenge. Each LMSR market must be funded up front in order to provide liquidity to market participants. This places a significant burden on the party that needs to provide the funding.

Bonding Curve Futarchy

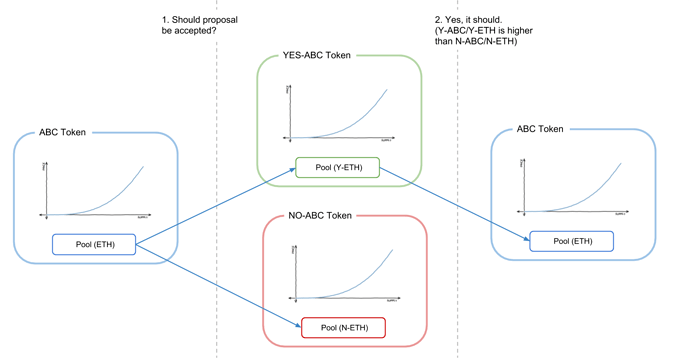
A bonding curve token has a built in price-finding mechanism as well as a reserve pool of funds. This can be used to create a relatively simple and self-contained futarchy mechanism. The mechanism works like this:

  1. Start with a bonding curve token ABC where its bonding curve uses ETH as the reserve token.
  2. A decision to accept a new proposal is started with a YES or NO outcome.
  3. Two tokenized events are started allowing the conversion of ABC into the outcome tokens YES-ABC and NO-ABC and ETH into YES-ETH and NO-ETH. If the decision is YES, YES-ABC tokens can be exchanged for ABC tokens and YES-ETH can be exchanged for ETH. Likewise, if the decision is NO, NO-ABC tokens can be exchanged for ABC tokens and NO-ETH can be exchanged for ETH.
  4. The main bonding curve is halted and two new bonding curves are created that mint YES-ABC and NO-ABC in exchange for their respective reserve tokens YES-ETH and NO-ETH.
  5. The main bonding curve’s reserve (ETH) is split into YES-ETH and NO-ETH and is used as the reserve for the YES-ABC and NO-ABC bonding curves respectively.
  6. Participants trade on the YES-ABC and NO-ABC curves predicting the value of ABC if the proposal is accepted on not accepted.
  7. The decision is resolved using a normal futarchy decision function such as highest price over the last 24 hours.
  8. The winning bonding curve’s reserve pool is converted back into ETH through the tokenized event and is used as the reserve for the main ABC bonding curve once again. The winning outcome tokens can be exchanged for ABC and the main ABC bonding curve can resume trading as normal.

1412×733 71.9 KB

Drawbacks

  1. It doesn’t work for normal tokens that don’t have a bonding curve.
  2. Allowing the main bonding curve to function during a decision is an unsolved problem and may not be possible.
  3. Bonding curves (as well as LMSR markets) are susceptible to front running.
  4. New decisions may create a race to be the first to buy into the new bonding curve.
6 Likes
2

While the bonding curve token thing may be an interesting solution to some set of problems, it doesn’t solve the hard part of Futarchy which is defining governance questions that have clear metrics of success and failure that can be reported on/agreed on after the fact even in the face of many confounding variables.

3

Hey. So, this split: it’s freezing ETH/ABC curve and creating basically two “version” of reality. Those who have ABC get Y-ABC & N-ABC. The immediate action that is possible is simply to sell into the underlying curve, correct? eg Y-ABC to Y-ETH or N-ABC to N-ETH? There’s no possibility get NEW liquidity into the pools whilst it is being traded/decided, correct? So the curves would effectively have a ceiling price until it’s closed?

If so, if a side wants to get “out” they can sell their token, say N-ABC to N-ETH and then sell/trade N-ETH to whoever wants to get that to buy back into N-ABC?

4

Maybe this deserves a new post to discuss confounding variables in futarchy decisions? We started talking about it here but didn’t get very far. Possible Futarchy Setups

Someone could actually buy in as well if they have some ETH by splitting it into Y-ETH and N-ETH and buying in to one or both of the curves. The Y-ETH or N-ETH for the winning decision’s reserve pool will then be turned back into ETH and become the reserve pool of the original ETH/ABC curve.

5

Very interesting idea. I think the third drawback of bonding curves being susceptible to front-running can mostly be solved with the solutions discussed in this article of a max gas price and allowing for limit orders.

2 Likes