TL;DR: We investigate how well randomly generated numbers can be used asas RSA moduli to have good RSA moduli with unkown factorisation to base Wesolowski vdfs (verifiable delay functions) on. Of course, these random numbers have a non-negligible probability of being easy to factor, but by including enough of them in a combined modulus we can reduce this to almost zero. For example, using an aggregate modulus length of ca. 81 kbits, we can reduce the probability that all the moduli included are less than 10^12 times more difficult than the currently known records using GNFS and ECM factorisation to 10^-12.
Motivation
Verifiable delay functions (vdfs): Verifiable delay functions are functions that require an amount \Delta of sequential work to be computed, with the property that a proof/witness can be provided that can be evaluated in time exponentially less than \Delta. These functions are currently considered because they allow the construction of blockchain-based random number generators that exclude any realistic chance for any of the participants to manipulate the entropy in their favour.
Wesolowski vdf: The Wesolowski scheme [Wesolowski 2018, https://eprint.iacr.org/2018/623.pdf] is a verifiable delay function based on the RSA crypto primitive. It requires an RSA modulus N that is not prime and of which the factorisation is unknown to all participants. An ideal modulus of size 2b would be a semiprime, a product of two prime factors with b bits; however, any modulus will do as long as it is extremely hard to factor using current algorithms and hardware.
Constructing RSA moduli: Currently, there are a few ways to construct suitable RSA moduli with unknown factorisation:
-
Trusted dealer: Appoint a trusted party to generate two primes of size b bits, compute their product, and erase all data (especially the two primes) afterwards. Obviously, it is very hard to find a person that everyone in the network would trust. In the blockchain setting, we would also want future users to trust that the dealer was honest. This is very difficult as they would not have been involved in the process.
-
Random moduli: If we generate a random number of a certain size b, there is a chance that it will already be a safe modulus, meaning that it is so hard to factor that it can be considered safe. Using only a single number, there is a serious chance that it might be factorable; however, by using several numbers in parallel, we can reduce the probability that all moduli are bad. As long as one of them is a good modulus, the Wesolowski vdf works as intended.
-
MPC: Multi-party computations can potentially generate a modulus in a cooperation of 100s or1000s of participants, where the resulting modulus is safe as long as at least one of them was honest and destroyed their private data after the ceremony. This reduces the trust issue present in the first scheme.
We will focus on the “Random moduli” approach in this post. Random moduli are also called RSA UFOs (Unkown Factorisation Objects).
Safe RSA moduli
In order to define what constitutes a safe modulus, we have to look at the two state-of-the-art factorisation algorithms:
-
General Number Field Sieve (GNFS): This is the fastest known general purpose factoring algorithm. It scales with L_n\left[\frac{1}{3},\sqrt[3]{\frac{64}{9}}\right] where n is the number to be factored (see L-notation: L-notation - Wikipedia)
-
Elliptic curve factorisation (ECM): This is the fastest known algorithm for factoring out small factors of n; if p|n is the smallest prime factor in n, then the run time to find p is L_p\left[\frac{1}{2},\sqrt{2}\right].
Given a random number, there will be some factors which can be stripped by a dedicated attacker using the ECM method. However, the modulus is still safe, as long as after all factors that can be removed in this way, the remaining modulus is still hard to factor by GNFS.
Picking the difficulty level
We have to pick a difficulty level in order to more precisely define what a good modulus is. In order to do this, we consider the current records in factorisation, and using the asymptotic complexities of the factorisation method, we choose a bit size that is 10^{12} (10^{9}, 10^{15}) times harder to factor than the given record as a “safety margin”.
For GNFS, the current record is the 768-bit number RSA-768, and the largest factor found using ECM has 274 bits [https://members.loria.fr/PZimmermann/records/factor.html]. Using the asymptotic expressions above, we can get the following (rounded) number of bits for the three selected difficulty levels:
-
Difficulty 10^{12}: ECM 621 bits, GNFS 2027 bits
-
Difficulty 10^{9}: ECM 523 bits, GNFS 1643 bits
-
Difficulty 10^{15}: ECM 727 bits, GNFS 2460 bits
Now we can define more precisely what a safe modulus is: E.g. at difficulty level 10^{12}, a modulus is safe if, after removing all factors of size less than 621 bits, the remaining “rough” (i.e. difficult to factor) part has more than 2027 bits.
Counting function
Suppose we start with a number of size b bits, and we want to estimate the probability that it is a safe modulus according to our definition. We can define the function
\displaystyle f(x,y,z) = \sum_{x/2<n\leq x, x \text{ is a good modulus wrt ECM factor size } y \text{ and GNFS factor size }z} 1
which counts the number of good moduli in the range from x/2 to x.
Removing numbers with small factors
We can improve our chance on picking good moduli by trying to factor the random numbers as far as possible. It is feasible to find factors up to size of ca. 180 bits using ECM on general purpose hardware. If we find any such factor, we can discard the number and pick a different one. As the size of the “remaining” modulus would be smaller than our ideal size, it would not be optimal to continue using it. If we define
\displaystyle g(x,a) = \sum_{x/2<n\leq x, x \text{is prime or has a factor less than } a} 1
Using this, we can find the probability of having generated a bad (i.e. unsafe) modulus as
p_\text{bad}(x,y,z,a) = \frac{f(x,y,z)}{x/2 - g(x,a)}
Scaling behaviour: (unproven but very likely from our knowledge about distribution of prime factors): p_\text{bad}(x^n,y^n,z^n,a^n) \approx p_\text{bad}(x^m,y^m,z^m,a^m) as m and n\rightarrow \infty.
Choosing the optimal bit size
The function p_\text{bad}(x,y,z,a) is monotonically decreasing in x. However, that does not mean for a given number of bits, the best way to get a safe modulus is to just generate one very large random modulus. Rather, if we create n moduli of size b, then the probability that the combined modulus is bad is equal to the probability that all moduli are bad: p_\text{bad}^n. To optimally use all the bits in such a combined modulus to minimize this probability, we want to maximize the function
\displaystyle F(x,y,z,a) = -\frac{p_\text{bad}(x,y,z,a)}{\log(x)} ,
i.e. find the x=2^b such that F is maximal.
Monte-Carlo simulations
To find the optimal bit size (depending on the difficulty level), we can use Monte-Carlo simulations. Thanks to the scaling behaivour of p_\text{bad}, we don’t actually need to use factored numbers with 1000s of bits to do this, even using 100 or 200 bits can give reasonable results, and these can easily be factored using open source algorithms, e.g. msieve [Msieve download | SourceForge.net]. However, to get better results, we can use specialised algorithms that generate uniformly distributed random numbers, for example the Bach algorithm [Bach 1988, https://dl.acm.org/citation.cfm?id=45475]. This gives more accurate results as well as allowing testing “in range” at the final bit sizes.
Results
I used the Bach algorithm to generate 10 million 1000 bit factored numbers. [ethereum/research pull request: Find optimal bit size for RSA UFOs by rcconyngham · Pull Request #95 · ethereum/research · GitHub]
Here are the results with optimal UFO sizes:
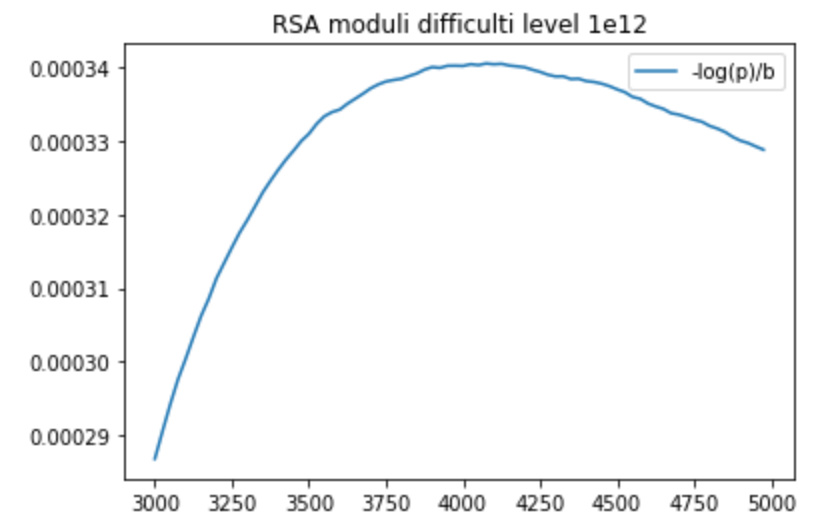
Difficulty level 10^12
Best value: p_bad = 0.249686420221 at 4075 bits
Modulus length for 1e-9 chance of bad modulus = 60860.7550651
Modulus length for 1e-12 chance of bad modulus = 81147.6734202
Modulus length for 1e-15 chance of bad modulus = 101434.591775
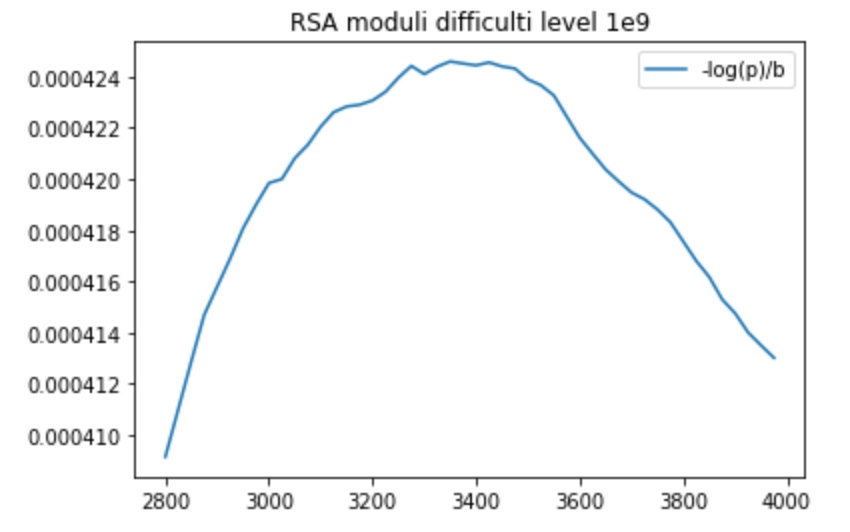
Difficulty level 10^9
Best value: p_bad = 0.241134127927 at 3350 bits
Modulus length for 1e-9 chance of bad modulus = 48806.8372042
Modulus length for 1e-12 chance of bad modulus = 65075.7829389
Modulus length for 1e-15 chance of bad modulus = 81344.7286736
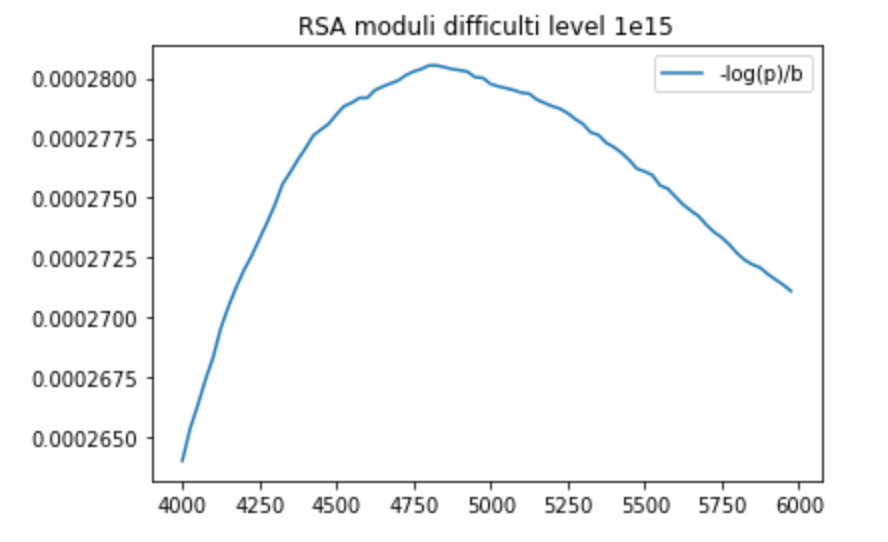
Difficulty level 10^15
Best value: p_bad = 0.258312650199 at 4825 bits
Modulus length for 1e-9 chance of bad modulus = 73870.3419613
Modulus length for 1e-12 chance of bad modulus = 98493.7892818
Modulus length for 1e-15 chance of bad modulus = 123117.236602