Masato Tsutsumi (Waseda University) (X: grandchildrice)
latest version: GKRFold: SumFold-based GKR Proof Compression - HackMD
Disclaimer: This post is in an early idea stage, and the logic and mathematical formulations may not be fully rigorous. We welcome any comments or feedback on the idea itself, as well as suggestions regarding the logical structure.
Abstract
In this paper, we introduce GKRFold, a protocol for compressing both the proof size and the verification cost of n GKR-based SNARK proofs. GKRFold incorporates SumFold—a component originally proposed in NeutronNova[KS24]—to achieve this compression. Ultimately, the compression process yields a single Sumcheck instance along with one commitment. As a result, the verifier is required to perform only one Sumcheck and two random polynomial evaluations. Moreover, the protocol is applicable to both uniform and non-uniform instances of the GKR protocol.
1. Introduction
1.1. GKR Protocol
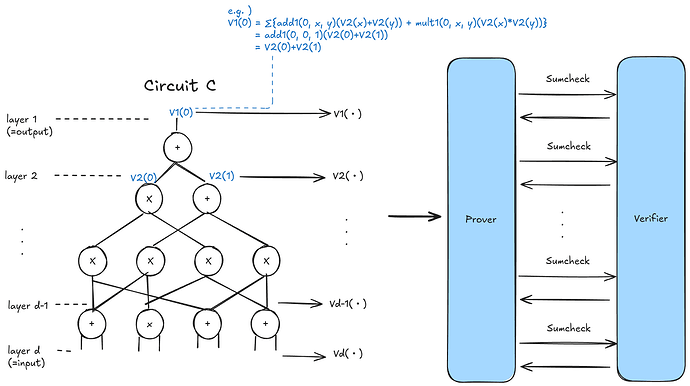
The GKR proof system[GKR15,XZZ19], a prominent SNARK (Succinct Non-interactive ARgument of Knowledge) due to its efficient prover time, has been employed in systems such as Expander and Ceno. Its design is based on representing each circuit layer as a corresponding layer polynomial. Starting from the output, the protocol sequentially relays a claim about one layer to a claim about the subsequent layer by executing a Sumcheck protocol on the evaluation of the layer polynomial at a randomly chosen point.
More precisely, the layer polynomial ( V_i ) is defined as
where the functions add_i(z,x,y) and mult_i(z,x,y) return 1 if the gate (z,x,y) in layer i is an addition or multiplication gate, respectively, and 0 otherwise.
An overview of the GKR protocol is as follows:
- The prover sends the circuit evaluation C(x,w)=y to the verifier.
- For every layer i = 1,\dots,d-1 (excluding the input layer), the verifier issues a challenge by selecting a random point r_i and then initiates the Sumcheck protocol on V_i(r_i).
- The verifier directly evaluates the input layer V_d(r_d).
Although the prover can generate proofs in O(N) time without committing to intermediate results or relying on FFTs, the verification time and proof size exhibit a complexity of O(D\log N). Consequently, achieving efficient proof compression remains an important challenge.
1.2. NeutronNova and SumFold
SumFold, as introduced in NeutronNova[KS24], is a technique that folds an arbitrary number of Sumcheck instances into a single instance. By applying SumFold to the GKR protocol, it is possible to compress the multiple Sumcheck instances inherent in GKR proofs, thereby reducing both the overall proof size and the verification time.
1.3. Contributions
In this work, we propose GKRFold, a novel method that applies SumFold to efficiently compress n instances of GKR proofs. The primary contributions of this study are as follows:
- We demonstrate that SumFold can be effectively utilized to compress GKR instances, leading to substantial improvements in proof size and verification efficiency.
- We show that GKRFold can compress n GKR proofs, each comprising d layers (amounting to a total of 6 \times n \times d Sumcheck instances), into a single Sumcheck instance.
This result significantly reduces the overhead associated with verifying multiple GKR proofs, making the protocol more practical for applications requiring succinct and efficient verification.
2. SumFold: High-Level Idea
The explanation of MLE, Sumcheck, and GKR is omitted here. Those who wish to study the details should refer to the following documents.
- https://eprint.iacr.org/2013/351.pdf
- Sumcheck - JoltBook
- https://www.youtube.com/watch?v=lMo-MmJ7e_E
- https://eprint.iacr.org/2019/317.pdf
- https://www.youtube.com/watch?v=lMo-MmJ7e_E
Assume that we wish to prove, via Sumcheck, a function defined by a composition
where F is a polynomial in t variables and \vec{g} is a vector of t polynomials in l variables. For example, one may consider the case
which represents the product of the components of \vec{g}(x).
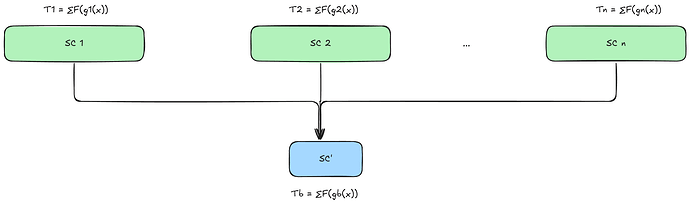
The goal of SumFold is to reduce the proofs of n Sumcheck instances
to a single Sumcheck proof.
We define a Sumcheck instance \mathsf{SC} that contains all the information required for a Sumcheck proof as follows:
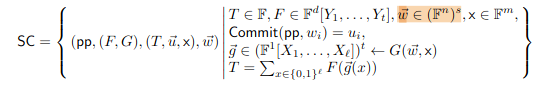
SumFold folds the n instances of \mathsf{SC} into one. The main idea behind SumFold consists of the following steps:
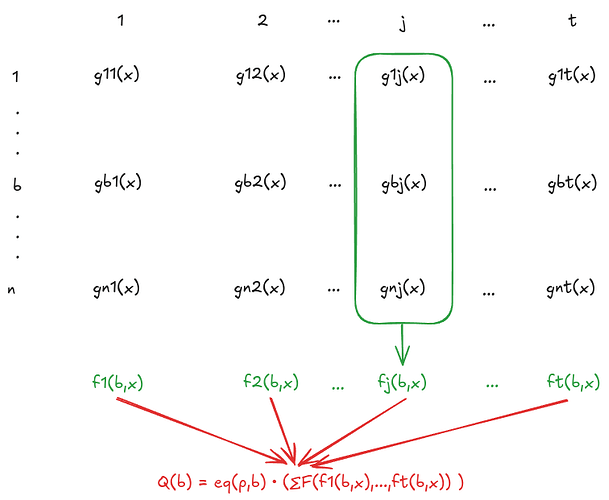
- For all i = 1,\ldots,n, givenT_i = \sum_x F(\vec{g}_i(x)),construct a polynomial Q(b) by interpolation such that, for any input b,Q(b) = T_b.This is achieved as follows:
- (a) Construct t polynomials f_j(b,x) via polynomial interpolation, where each polynomial outputs g_{bj}(x) corresponding to the $b$th instance.
- (b) Reconstruct Q(b) by applying the function F to the collection \{f_1(b,x), \dots, f_t(b,x)\}.
- Commit to the polynomial Q(b). This commitment effectively aggregates the commitments for all n Sumcheck instances.
- The verifier selects a random challenge r_b and designates the $r_b$th Sumcheck instance as the folded instance.
It is verified (see Appendix B of the NeutronNova paper[KS24]) that
Protocol (cited from [KS24]):
3. GKRFold
3.0. Linear GKR Protocol (Libra[XZZ19])
In this section, we describe the linear-time algorithm for the GKR protocol. First, assume that the following layer polynomial is given:
We partition this expression into three terms:
For each term, a 2-phase Sumcheck protocol is executed. For instance, consider the third term:
where
The 2-phase Sumcheck protocol is then carried out as follows:
- Prove the correctness of h_{i+1}(x) via Sumcheck.
- Prove the correctness of the term \sum_{x \in \{0,1\}^{S_i}} h_{i+1}(x)V_{i+1}(x) via Sumcheck.
Thus, for each layer, a total of 2 \times 3 = 6 Sumcheck instances are executed in parallel.
3.1. GKRFold: Overview
Assume that we are given n GKR instances, and that each instance comprises d layers. Then there exist a total of n \times d layer polynomials. For each layer, the protocol requires 6 Sumcheck instances (as described above), resulting in a total of
Sumcheck instances.
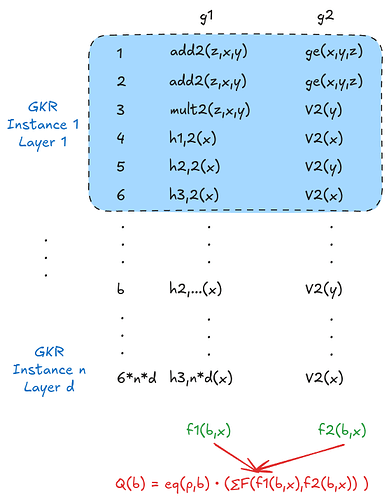
These six types of Sumcheck instances are summarized in the following table:
| Sumcheck 1 (h_{1,i+1}(x)) | Sumcheck 2 (h_{2,i+1}(y)) | Sumcheck 3 (h_{3,i+1}(x)) | Sumcheck 4 (1st term) | Sumcheck 5 (2nd term) | Sumcheck 6 (3rd term) | |
|---|---|---|---|---|---|---|
| Expression | \sum_{y \in \{0,1\}^{S_i}} add_{i+1}(z,x,y) | \sum_{x \in \{0,1\}^{S_i}} add_{i+1}(z,x,y) | \sum_{y \in \{0,1\}^{S_i}} mult_{i+1}(z,x,y)V_{i+1}(y) | \sum_{x \in \{0,1\}^{S_i}} h_{1,i+1}(x)V_{i+1}(x) | \sum_{y \in \{0,1\}^{S_i}} h_{2,i+1}(y)V_{i+1}(y) | \sum_{x \in \{0,1\}^{S_i}} h_{3,i+1}(x)V_{i+1}(x) |
| Form of F | F(g_1(x),g_2(x)) = g_1(x) \cdot g_2(x) | same | same | same | same | same |
| Vector \vec{g} | \{ add_{i+1}(z,x,y),\, g_e(x,y,z) \} | \{ add_{i+1}(z,x,y),\, g_e(x,y,z) \} | \{ mult_{i+1}(z,x,y),\, V_{i+1}(y) \} | \{ h_{1,i+1}(x),\, V_{i+1}(x) \} | \{ h_{2,i+1}(y),\, V_{i+1}(y) \} | \{ h_{3,i+1}(x),\, V_{i+1}(x) \} |
Note that Sumcheck 1 and Sumcheck 2 naturally have the form
However, by introducing the constant identity function g_e(x) = 1 (which always returns 1), they can equivalently be expressed as
Thus, all Sumcheck instances share the same functional form
The correspondence between these Sumcheck instances and the SumFold framework is given in the table above.
Consequently, by applying SumFold, the total of
Sumcheck instances can be folded into a single Sumcheck instance.
3.2. GKRFold: Protocol
Input:
n GKR instances, represented as
Output:
(SC,\, r_b,\, \bar{Q}(r_b),(\vec{x}_i, \vec{w}_i), (\vec{u}_i))
Protocol:
-
The prover sends the evaluation results C_i(x,w) = y for each instance to the verifier.
-
Based on the layer polynomials V_i, assign the six Sumcheck instances (SC1 through SC6) for each layer.
-
Execute SumFold under the following conditions:
-
The function is defined as
F(g_1(x), g_2(x)) = g_1(x) \cdot g_2(x). -
The vector \vec{g} is instantiated as follows:
- SC$_1$: \{ add_{i+1}(z,x,y),\, g_e(x,y,z) \}
- SC$_2$: \{ add_{i+1}(z,x,y),\, g_e(x,y,z) \}
- SC$_3$: \{ mult_{i+1}(z,x,y),\, V_{i+1}(y) \}
- SC$_4$: \{ h_{1,i+1}(x),\, V_{i+1}(x) \}
- SC$_5$: \{ h_{2,i+1}(y),\, V_{i+1}(y) \}
- SC$_6$: \{ h_{3,i+1}(x),\, V_{i+1}(x) \}
-
-
Verify that for all i = 1, \dots, n,
Q(6d \cdot i) = v_{i,d}(r_d),where Q is the polynomial constructed via SumFold and v_{i,d}(r_d) denotes the evaluation of the corresponding layer polynomial at the challenge r_d.
-
The verifier evaluates the input layer V_d(r_d).
3.3. Proof of Theorem
We will describe the details in a later paper, but it should be possible to prove that completeness, soundness, and zero-knowledge properties are satisfied according to SumFold.
3.4. Cost
Let
- d denote the number of GKR layers,
- t = 2 denote the number of variables in F,
- D denote the degree of F,
- n denote the number of GKR instances, and
- l denote the number of variables in g.
The complexities are summarized in the following table:
| Round | Communication Complexity | Prover Time Complexity | Verifier Time Complexity |
|---|---|---|---|
| 1+\log(nd) | O(D \log(nd)) field elements | O(nd \cdot t \cdot 2^l) field elements | O(D \log(nd)) field elements |
By following Theorem 2 in the NeutronNova paper[KS24]:
Acknowledgement
Special thanks to yugo for discussing GKR Recursion during the hackathon and providing feedback on ideas in the early stages of this research.