Gossipsub Network Diameter Estimate

Networking
1

TL;DR

The ProbeLab team (probelab.io) has been working extensively on the behaviour of Gossipsub in the Ethereum network (see recent posts). We now present a new stochastic, theoretical model to estimate how quickly messages travel across a Gossipsub network (its diameter). By focusing on a broadcast-only approach with a fixed mesh degree and random connections, our analysis found that the Gossipsub diameter of the Ethereum network is seven.

Introduction

In this post, we develop a theoretical model for estimating the diameter of a Gossipsub network. By “diameter,” we refer to the maximum number of hops (or discrete time steps) required for a message to reach all nodes in the system. This metric provides direct insight into how quickly broadcasts propagate across the network. Additionally, understanding the diameter helps reason about redundant (duplicate) messages and offers guidance on how to optimize the protocol to minimize unnecessary overhead.

Analyzing network diameter and duplicate messages ratio yields practical benefits:

  • Performance assessment: Quantifying propagation speed allows us to gauge whether nodes receive critical data in a timely fashion.
  • Protocol optimization: Observing the duplicate messages distribution can uncover opportunities to reduce bandwidth consumption and network congestion.
  • Resilience insights: Knowing the worst-case propagation paths can guide improvements that bolster reliability under various stress conditions.

To focus our analysis, we make several assumptions:

  • Broadcast-only model: We consider just the pub-sub (broadcast) aspect of Gossipsub, ignoring its “gossip” component.
  • Constant mesh degree: The mesh degree D is fixed for every node in the network.
  • Random graph topology: Each node connects to exactly D peers, chosen at random. All links are bidirectional, ensuring the graph is connected.
  • Static mesh: The mesh is assumed to remain static during the propagation process.
  • Uniform link latency: All peers are equidistant from each other in terms of network latency.

These assumptions enable a stochastic model that remains tractable while still capturing key properties of the Gossipsub network. In the following sections, we develop this model step by step, and illustrate its implications for message propagation.

Intuition

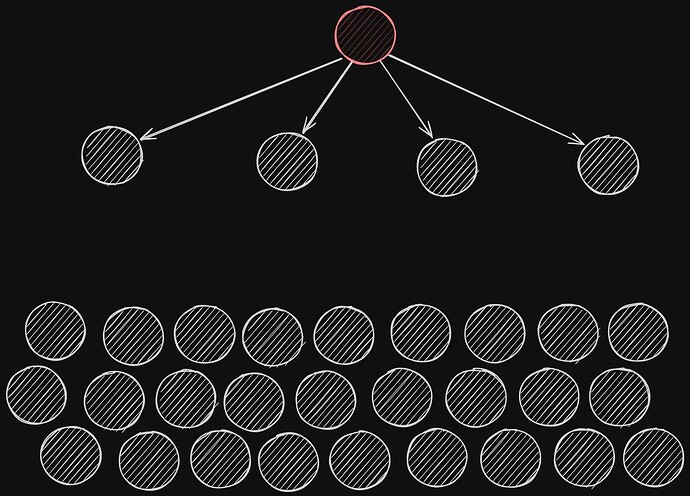
Let’s consider a simple illustration of how a message propagates through a network where each node has four connections (D=4). When a node receives the message for the first time, we say it becomes “infected.” In the following round, that newly infected node sends the message to its own neighbors, who in turn become infected. Step by step, we see how the broadcast ripples through the network until all nodes have received the message.

Round 0

At the very start, we have exactly one “infected” node holding the message.

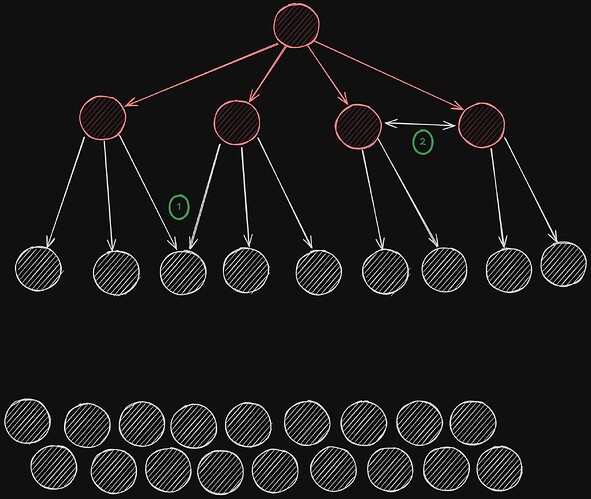
Round 1

In this round, the original node sends the message to its D=4 neighbors. Those four nodes become “infected” and are now aware of the broadcast. They will, in turn, propagate the message in the next round.

Infection process: round 1
Infection process: round 11920Ă—1382 213 KB

Round 2

Each of the four newly infected nodes repeats the broadcast, sending it to their own three remaining neighbors. (1) Note that two peers may try to infect the same node, which hasn’t been infected yet. (2) Also note that two nodes that have been infected in the previous round may be connected to each other, and try to infect each other, even though they are both already infected.

It is important to take into account these 2 kinds of duplicates when computing the number of nodes infected in the next round.

Infection process: round 2
Infection process: round 21920Ă—1623 204 KB

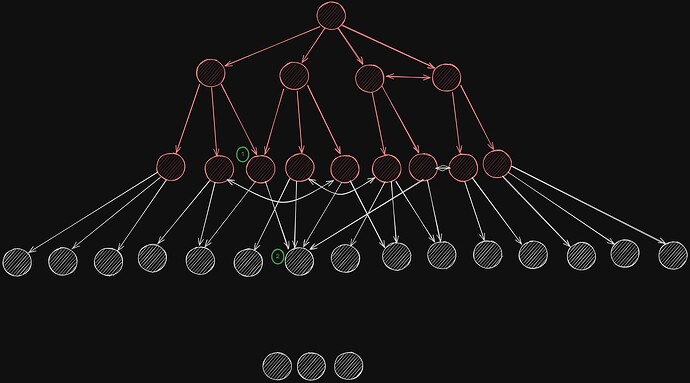
Round 3

By the third propagation step, most or all of the reachable nodes (in our simple example) will have been infected. (1) Note that the node that was infected twice in the previous round is only able to infect two additional nodes, and not three. This is so because all nodes have exactly D=4 connections, and the number of outgoing messages is exactly D minus the number of incoming messages. (2) Similarly, a node being infected 4 times, will not try to infect any other node at the next round, since it doesn’t have extra links.

As the number of infected nodes grows, so does the number of duplicates.

Infection process: round 3
Infection process: round 31920Ă—1068 99.2 KB

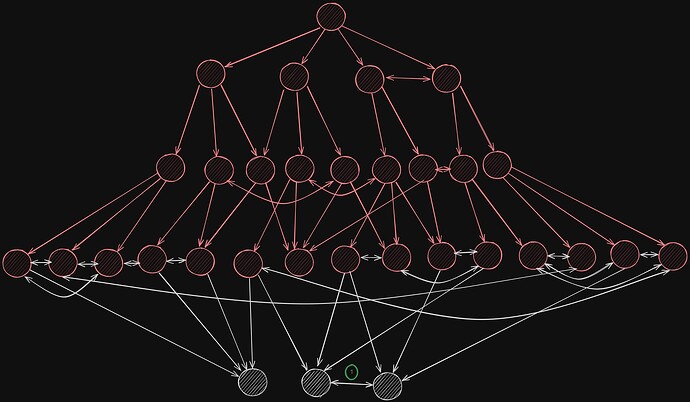
Round 4

By the fourth and last propagation step, all nodes have been infected. We observe that at this point the vast majority of infections are actually duplicates. (1) Note that nodes infected in the last round can be connected to each other, which means that there would be a fifth round in which these nodes are infecting each other again. However this round doesn’t count toward the network diameter, since all nodes have been infected at this point.

Infection process: round 4
Infection process: round 41920Ă—1120 123 KB

The maths

Our goal is to determine, at each round t, how many nodes become newly infected given the count of newly infected nodes in round t-1. Tracking this progression across rounds reveals the point at which all N nodes in the network have received the message, thereby allowing us to estimate the network’s diameter.

Duplicates

As stated above, we distinguish between two main sources of duplicate infections: same-layer connections and next-layer collisions.

  1. Same-layer connections

    These occur between pairs of nodes that both become infected in the same round and also share an edge. When these nodes attempt to infect each other in the following round, no new infections result because they are already infected.

  2. Next-layer collisions

    These arise when a node receives multiple initial infections during the same round. Since each node has a fixed mesh degree D, each “extra” infection effectively reduces the number of fresh nodes it can infect in the next round. Put differently, a node that is already infected by multiple peers cannot use those same edges to infect additional new peers in subsequent rounds, thereby diminishing its overall infecting capability.

Definitions

  • N: number of nodes in the network
  • t: The discrete round number (t=0,1,2,...).
  • I(t): The number of nodes that become infected for the first time during round t
  • R(t): The total (cumulative) number of nodes infected on or before round t. Formally:
R(t) = R(t-1) + I(t)
  • C(t): The number of next-layer collisions occurring in round t. A collision occurs when a node is infected multiple times during the same round. For example, if a node is infected three times at round t, it contributes 3-1=2 to C(t), as only the first infection counts as a new infection, and the remaining 2 are redundant.

Initial case

At t=0, we start with a single infected node, which it the one publishing the message, hence

I(0)=1, R(0)=1, C(0)=0

At t=1, the single infected node from round 0 infects its D neighbors. There are no next-layer collisions since all nodes to which the initial node is connected are distinct. Therefore,

I(1)=D, R(1)=D+1, C(1)=0

Inductive Step

Starting from t=2, both same-layer connections and next-layer collisions are possible.

At round t, the number of infection attempts x_t is given by:

x_t = (D-1) \times I(t-1) - C(t-1)

This formula accounts for the following:

  1. Each node that was infected exactly once in the previous round (I(t-1)) has D-1 remaining links available for new infection attempts.
  2. We subtract the next-layer collisions from the previous round (C(t-1)) because those connections were already consumed during the previous round’s multiple infections and cannot be reused.

This adjustment ensures that x_t reflects only the valid, unused links available for new infections in the current round.

Let’s define the number of nodes that haven’t been infected yet at the start of round t.

M_t=N-R(t-1)

We can now calculate how many infection attempts reach the next layer (including next-layer collisions) by determining the probability that each connection of round t is not a same-layer connection.

y_t=x_t \times \frac{M_t}{N-R(t-2) -1}

Here’s the reasoning:

  • Nodes infected at round t-1 can potentially connect to any of the N-R(t-2)-1 other nodes in the network (excluding themselves).
  • Among these, M_t=N-R(t-1) nodes are still uninfected and thus eligible for new infections.
  • The remaining I(t-1)-1 nodes represent infections that occurred during round t-1. These nodes could form same-layer connections, which would not create new infections.

The number of same-layer connections is as follows

x_t \times \frac{I(t-1)-1}{N-R(t-2)-1} = x_t - y_t

To compute the number of new infections, we must account for and discard duplicates.

The probability that a single infection attempt successfully targets a specific node among the M_t eligible nodes is:

Pr[\text{infecting a specific node}] = \frac{1}{M_t}

The probability of not infecting this specific node in a single attempt is:

Pr[\text{not infecting a specific node}] = 1 - \frac{1}{M_t} = \frac{M_t-1}{M_t}

If y_t infection attempts are made, the probability that a specific node is never infected is:

Pr[\text{not infecting a specific node in } y_t \text{ attempts}] = (\frac{M_t-1}{M_t})^{y_t}

Thus, the probability of infecting this specific node at least once in y_t attempts is:

Pr[\text{infecting a specific node in } y_t \text{ attempts}] = 1-(\frac{M_t-1}{M_t})^{y_t}

Since there are M nodes eligible for infection in the current round, the expected number of fresh infections is:

I(t) = \mathbb{E}[\# \text{ distinct newly infected peers}] = M_t \times [1-(\frac{M_t-1}{M_t})^{y_t}]

The number of next-layer collisions can then be computed as the difference between the total infection attempts and the number of newly infected nodes:

C(t) = y_t - I(t)

And the total number of duplicates at round t, D(t) is the sum of the next-layer collisions and same-layer connections.

D(t) = (y_t - I(t)) + (x_t - y_t) = x_t - I(t)

With these formulas, we now have all the components needed to run the model.

Results

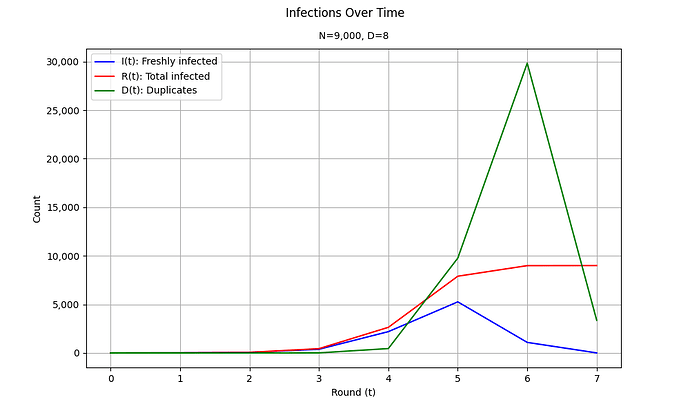
In the Ethereum network D=8 (source), and N \approx 9,000 (source). For these parameters, we obtain the following results:

Gossipsub message propagation over time in the Ethereum network
Gossipsub message propagation over time in the Ethereum network1000Ă—600 37.8 KB

t= 0,  I(t) =      1.00,  R(t) =      1.00,  D(t) =      0.00
t= 1,  I(t) =      8.00,  R(t) =      9.00,  D(t) =      0.00
t= 2,  I(t) =     55.79,  R(t) =     64.79,  D(t) =      0.21
t= 3,  I(t) =    379.67,  R(t) =    444.46,  D(t) =     10.66
t= 4,  I(t) =  2,195.63,  R(t) =  2,640.08,  D(t) =    453.79
t= 5,  I(t) =  5,262.28,  R(t) =  7,902.36,  D(t) =  9,765.61
t= 6,  I(t) =  1,089.18,  R(t) =  8,991.54,  D(t) = 29,836.48
t= 7,  I(t) =      8.14,  R(t) =  8,999.68,  D(t) =  3,367.09

Python simulation code

Network Diameter

After seven rounds, an average of 8,999.68 nodes (out of 9,000) become infected, indicating that in some instances, an additional round might be required to reach the last remaining node. Based on these results, it is reasonable to consider the network diameter to be seven under these conditions.

Infections

As expected, the number of new infections rises steadily until round five, where it reaches a turning point. Afterward, it begins to decline as the pool of uninfected nodes shrinks and becomes harder to reach.

Duplicates

A particularly noteworthy observation is the surge in duplicate messages during rounds five and six. This spike occurs because many nodes are newly infected in the previous round, yet there are fewer uninfected targets available, resulting in more redundant transmissions.

Each node is expected to send and receive an average of D-2 duplicates (source). However, when we apply this model to the Ethereum network, we see an average of about 4.83 duplicates per node (roughly D-3). This discrepancy occurs because our stochastic model, which works in discrete steps, doesn’t fully capture the timing-dependent nature of duplicates. Nevertheless, we expect the model to accurately represent how duplicates are distributed, especially since a larger number of duplicates tend to appear in the later stages of message propagation.

Conclusion

We developed a stochastic model to approximate the diameter of GossipSub networks based on their mesh degree and overall size. Applying this model to the Ethereum network reveals a GossipSub diameter of seven. During this analysis, we also observed that the majority of duplicate messages are sent in rounds five and six, coinciding with the period when most nodes have just become infected yet there are fewer remaining targets.

3 Likes