Abstract
This document describes a hierarchical deterministic wallet scheme that works with lattice-cryptography.
Motivation
Hierarchical Deterministic Wallets HD-Wallets have become the de-facto standard in blockchain. As the blockchain industry discussed a post-quantum future, we would like to apply this technique to keys in a lattice cryptography setting, as the user experience of backing up a single seed phrase that generates unlimited a-priori-unconnected keys is highly preferable to users having to back up the same wallet each time an action is performed.
We focus on the Dilithium signature scheme as it was the first finalized NIST post-quantum-signature and is likely to become an industry standard.
The challenge with adapting lattice cryptography to an HD setting is two-fold. First is that the output of an HMAC-SHA512 cannot be used as-is for a lattice private key. For Falcon and Dilithium
we need polynomials that form a “good basis” (small vectors) for the lattice, and the key generation algorithms use rejection sampling, which does not fit into the HD wallet scheme without modification.
The second challenge is that, in BIP32, non-hardened keys are derived via addition of elliptic-curve points (public keys) and there is no such equivalent operation for lattices: the set of lattice public keys are not closed under addition or multiplication.
We address the first challenge in this QIP and do not attempt to support non-hardened keys. It is, to our knowledge, an open research question whether this second challenge can be overcome in the lattice cryptography setting. Non-hardened keys are used for watch-only or audit wallets and are not essential to the primary use of HD-Wallets, so we do not see this as a critical drawback.
Specification
The essential idea is to use the entropy output from HMAC at each iteration as the RNG for polynomial sampling. In BIP32, half of the output of the HMAC is used as the private key, either directly as in the “hardened” case, or added to the previous private key, in the “non-hardened” case. This works because of the structure of elliptic curve cryptographic algorithms, where the private key can be viewed as just an integer that is multiplied by the generator point in the elliptic curve group.
In both Falcon and Dilithium, the key generation algorithms consume <= 64 bytes of entropy in the key derivation process. We could simply feed the entire output of the HMAC into the key generation process, instead of using half as the private key itself, but to maximize interoperability with BIP44 wallets, we simply use half the output. This makes the scheme identical to hardened key derivation in BIP32.
This technique of using the seed as the default key format is supported by NIST here
Reference Implementation
The implementation of the lattice HD wallet lives here. We test against test vectors generated by pq-crystals, which is the reference implementation of dilithium, written in C by the authors of the standard.
Both wallet versions use the rust library bip39 to get from a mnemonic “seed phrase” to a “seed”. We then derive a “master key” from the seed via HMAC-SHA512 and that forms the root of the tree of keys, with each edge representing HMAC-SHA512(R || 0x00 || L || child_index) where L || R are the split values of the parent in the tree, as described in the BIP32 standard.
Rationale
We initially considered using Falcon, as it has smaller keys and signatures. For this, we relied on Thomas Pornin’s rust-fn-dsa implementation of the FALCON signature algorithm, with some minor modifications to allow for externally generated entropy. Thomas Pornin was one of the authors on the FALCON standard, and also the author of the PQClean C-lang implementation of the algorithm. The implementation of the Falcon wallet lives here.
It later came to our attention (from Thomas Pornin) that the Falcon standard does not completely specify the key generation path, so we have decided to switch to ml-dsa (formerly dilithium). Dilithium has several advantages. It is
- simpler
- faster
- has deterministic key generation
- has already been finalized by NIST
The downsides are the bigger keys, bigger signatures, and slower verification.
In any case, lattice keys and signatures are all much bigger than elliptic curves, so we will just have to pay for more disk space.
Both Dilithium and Falcon require <= 64 bytes of entropy as input to the key generation process, so we can simply use the first 32 bytes output of HMAC-SHA512 as an entropy source. The non-hardened use case is not obviously achievable with lattice cryptography, so we omit it.
Concerning the quantum-security of HMAC-SHA512, the primary quantum-attack against hash functions is Grover’s algorithm which provides a quadratic speedup on searching unsorted databased (hash pre-images in our case). This cuts the security bits in half, so 512 → 256, 256 → 128, etc.
This applies to all hash functions, so any classically-secure hash algorithm will have the same issue. On the other hand, it has been proven that Grover’s algorithm is asymptotically optimal, so we should not expect another quantum algorithm to do much better than Grover’s against a secure hash function.
In contrast to hash functions, the digital signatures of blockchains are much more vulnerable to quantum attacks, as Shor’s Algorithm reduces the difficulty of finding an elliptic curve private key from a public key from exponential (Pollard’s rho) to polylogarithmic O(log^3(n)), where n is the number of bits.
For this reason, we are prioritizing securing the digital signatures against quantum
attacks and leaving the hash functions unchanged.
Copyright
This specification is released into the public domain.
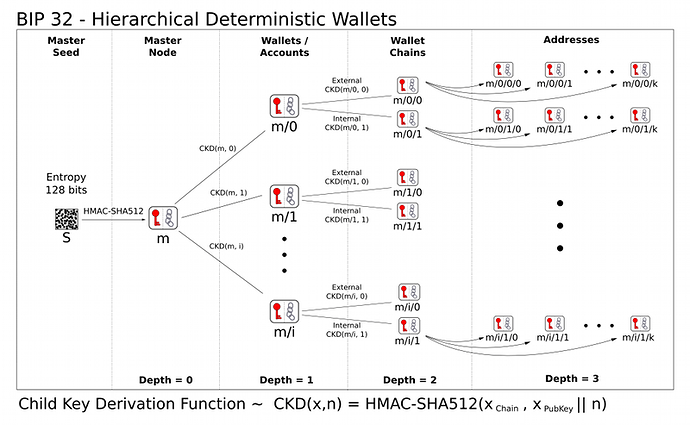
See this diagram for a summary of BIP32.
This proposal was originally posted as a Quantus Improvement Proposal here