TL;DR
We propose a protocol of verifiable formal verification of smart contracts, which provides a way for wallet apps, dapp browsers and even smart contracts to know whether a target contract is secure and satisfies certain specifications by SN[T]ARKs over formal verification. This would be a “https” in blockchain.
We discuss the use-cases, spec of protocols and technical challenges to realize this here omitting some parts for brevity. See this report for the omitted parts.
Version
0.2
Authors
LayerX Inc. R&D Team
Ryuya Nakamura (ryuya.nakamura@layerx.co.jp)
Osuke Sudo (osuke.sudo@layerx.co.jp)
Takeshi Yoneda (takeshi.yoneda@layerx.co.jp)
Takayuki Jimba (takayuki.jinba@layerx.co.jp)
1 Overview
1.1 Background
Currently, formal verification of smart contracts is executed in each computers. If someone formally verified some contracts, you have no way to verify that without executing the program of formal verification by yourself. Otherwise, all you can do is to trust the person who did the formal verification. Moreover, there is no way for a smart contract to judge whether the other contract is formally verified or not.
We propose a protocol to prove on-chain that a contract has been formally verified and satisfies certain specs with SN[T]ARKs. This protocol provides a way to verify a formal verification in a much less computational cost. Specifically, there are two types of benefits:
(1) Smart contracts can judge whether the other contract it’s about to call satisfy certain specs or not by themselves.
(2) Light clients like mobile apps can see whether the certain contract satisfy certain specs.
In other words, this protocol provides “https” in blockchain. Of course this doesn’t assure 100% that there would be no hacks but give some degree of security.
1.2 Abstract of protocol
In this protocol, a verifier contract(Verifier contract) verifies the SN[T]ARKs proof that proves a given EVM bytecode(i.e. ‘target’ contract) satisfies some set of specifications. If the verification succeeds, the verifier contract stores the target contract’s address or hash of its bytecode onto the storage. The number of verifier contracts corresponds to that of specifications they prove. If users or other contracts want to know whether a certain contract satisfies some specification, they could ask the corresponding verifier contract about it.
1.3 Use-cases
Here we provide examples of use-cases regarding each type of the benefits described in section 1.1.
(1) Crypto collateral system without vulnerable tokens
In some financial protocols like stable coins (e.g. Maker[1] and Reserve[2]) or derivatives (e.g. Dharma[3]), crypto assets including not only ether but also ERC20 tokens are used as a collateral. Even though these protocols handle the case when the price of such collaterals drop, if the contract on which these collateral assets based had bugs, like famous integer overflow or reentrancy, it could cause black swans and entire system might be broken.
This kinds of black swans would be removed if the system contracts of these protocols prevented from using tokens whose contracts are not formally verified from being included as collateral.
(2) Secure wallet apps or dapp browsers
Wallet apps or dapp browsers can protect users from using vulnerable contracts using (above mentioned) verification contracts. This is not limited to the check of such famous vulnerabilities like overflow. We think Layer 2 protocol like Plasma and state channel would have standards in the future. For example, L4 and Celer team are working together on the standardization of state channel[4]. These standards would be written as a formal specification amenable to formal verification. (see our experimental project[17] of formal verification of Plasma contracts with KEVM[5].) Therefore, with the protocol propose, wallet apps or dapp browsers can raise warning for users to tell the Plasma/state channel contracts are compliant with these standards.(e.g. “WARNING: This Plasma Cash contract is not standards-compatible.”)
2 Methodology
2.1 SNARKs over formal verification
We intend to use SNARKs as a non-interactive proof system because the proof size is so small and will fit well to the blockchain.
The proof size of SNARKs is only 288 bytes for 128 bits of security [6] [7] or approximately 131 bytes [8].
STARKs has advantage features over SNARKs like non-setup and proving cost, so we are also planning to use STARKs as a proof system in the future.
But here, we will discuss especially in the case of SNARKs.
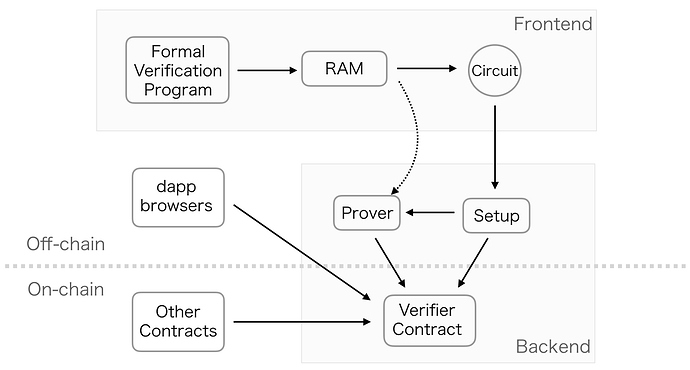
The verifier contract needs to be deployed in advance by the setup phase.
In the frontend, formal verification program is executed by RAM (random-access machine) which is general computational models, and the process generates the circuits for SNARKs.
In the backend, the generated circuits and the RAM are used for the SNARKs. The setup as a pre-processing generates the proving key and the verification key that are used in proving and verifying respectively.
Only if the prover passes the formal verified bytecode, the proof which is sent from the prover to the verifier will be accepted and return true by the verifier contract.
The fact will notify to the dapp browsers or be called by other contracts.
We formalize the program to be verified with SNARKs like:
Pprove(w = bytecode, x = hash(bytecode)) {return proof}
Pverify(proofkey, hash(bytecode)) = True/False
where
x: the primary input (which passes to on-chain computation)
w: the auxiliary input (which does NOT pass to on-chain computation))
bytecode: the bytecode of smart contract that you want to verify
proof_key: proof key of the formal verification result
Since contracts’ bytecodes are too huge in byte to be put into on-chain, we treat it as auxiliary input (in other words, private input) and take only its hash value as primary input (i.e. public input). The following snippet is the pseudo code of P_prove (i.e.the contract owner want to prove):
struct In {
// EVM byte code's hash
uintN_t bytecodeHash
// EVM bytecode as private input
uintN_t bytecode[MAX_BYTECODE_LENGTH]
}
struct Out {
// represents whether `bytecodeHash` is valid or not.
bool isValidBytecode
// represents whether the given bytecode is formally verified or not.
bool isValidContract
}
uintN_t hash(uintN_t bytecode[MAX_BYTECODE_LENGTH]) {
// [...]
return hash_of_byte_code
}
bool formallyVerifyBytecode(uintN_t bytecode[MAX_BYTECODE_LENGTH]) {
// [...]
return result_of_formal_verification
}
void compute( struct In *input, struct Out *output ) {
// 1. compute hash value of bytecode
uintN_t h = hash(input->bytecode)
// 2. check if the above calculated value equals the input bytecodeHash
output->isValidBytecode = (h == input->bytecodeHash)
// 3. check if there's a vulnerability in byte code
output->isValidContract = formallyVerifyBytecode(input->bytecode)
}
To convert this program into arithmetic/boolean circuits, we adopt computational models like TinyRAM which are already known to be converted into circuits. The formal verifier will be implemented over these computational models.
Note that the private input variables may include a proof, an object which express how formal verifier applied their rules of inference in addition to hash(bytecode). See (2) in section 3.2.
When the P_verify function returns true, the address of the verified contract is registered in the deployer contract or emits the event to notify the result to off-chain clients.
2.3 Set up
In both protocols above, verifier contacts need to be registered beforehand in the “trusted list” in the contract or mobile apps that use this protocol.
These protocol based on the correctness of verifier contracts, i.e.
- algorithm of formal verification
- formal specification to be verified
- circuits which represents the algorithm of formal verification
- verification program of SN[T]ARKs
3 Challenges & Solutions
3.1 Main Challenges
The most part of the difficulties to achieve this is around converting a formal verification program to circuits because formal verifiers are basically complicated programs. Most of the formal verification methodologies adopts Z3 as a SMT solver or uses interactive theorem provers like Coq or Isabelle and they are composed of complicated algorithms and have millions of lines of code.
More concretely, there are these two challenges.
(1) Implementation difficulty
There are several libraries like ZoKrates[10], xJsnark[11] and Pequin[12] to develop a program which can be compiled to circuits of SNARKs. They made it easier to compose circuits for normal programs, but their DSLs cannot be compared with usual programming languages like Java, Python or C++ in which formal verifiers implemented so to implement a formal verifier with their DSLs is quite difficult. In addition, they don’t have sufficient documents and most of them are not aimed for production use.
(2) Circuit complexity
SNARKs has a constant time of verification and a constant size of proof but the number of constraints increases as the complexity of a program increases. i.e. the time and cost of generating a proving key increases.
The computational cost of formal verification would be huge, so we need to optimize it and reduce the circuit complexity. Several libraries (like DIZK) have been developed to reduce the circuit complexity in the backend for SNARKs.
As an example, gnosis team estimates the costs is roughly 1200$ using AWS and DIZK about their SNARKs application of decentralized exchange. We need more optimization not only in the backend of SNARKs but also the frontend.
3.2 Solutions
(1) General computation
We are considering to implement a formal verifier on LLVM and compile it to RAM that can be converted to circuits. TinyRAM has a minimal ISA that enables to generate small circuit complexity. However, because it is too hard to implement the LLVM backend of TinyRAM, we will use the existing backend machine similar to TinyRAM.
One of the machine would be RISC-V which is a simple and has a restricted number of instruction set, so we think it can be used as a computational machine for the circuit generation. However, because of the larger instruction set of RISC-V the efficiency of the circuit generator might be lower than the one of TinyRAM and make the second challenge even more difficult.
(2) Less-computational formal verification algorithm
We need to adjust the algorithm of formal verification so that the implementation cost and the amount of circuits are reduced. One promising technique is to remove the proof search which require a huge computation and focus on the verification of a given proof. The softwares of formal verification find the proof, the sequence of their rules of inference automatically or semi-automatically with human’s help. However, the program converted to circuits in our protocol isn’t necessarily able to find the proof because the proof generated by off-chain formal verifier can be passed as a private input and all the program need to do is to verify the proof.
Another approach is to adopt some heuristics about certain vulnerabilities. For example, Securify[13] uses a pattern detection in the semantics of the target bytecode expressed their DSL and leverages the domain-specific insight that violations of many practical properties for smart contracts also violate simpler properties, which are significantly easier to check. The algorithm seems much more easier to convert to circuits than KEVM and interactive theorem provers. However, the specifications which can be verified with this kind of technique are limited. For example, the verification of “No overflow” property would be difficult without something like Z3.
4 Future work
We need more feasibility study about this project, especially about the challenges described in section 3. The most important point is the circuit complexity of formal verifier but it would be difficult to estimate without actually implementing it. Research on zero-knowledge proof systems including STARKs and others would also be important.
Our long-term goal includes:
- development of a infrastructure to do a SN[T]ARKs over a general computation (e.g. circuit generator of RISC-V)
- development of a formal verifier which is more SN[T]ARKs friendly
P.S
Two of the authors(Ryuya and Osuke) will attend DEVCON4. Let’s discuss about this if you are interested! Contact us.