Progress
Hi, all! We are from Orbiter Finance . Currently, we support transaction validity proofs for Ethereum, Arbitrum, Optimism, and zkSync Era. In addition to this, we also provide services for historical block validity proofs and account state proofs.
Advantages
- Low-gas: Due to our usage of PLONK for recursive proof composition in Halo2, the current gas consumption for on-chain proofs averages around 350,000 gas. On the other hand, uploading all the data and performing the computation within the contract on-chain would incur a minimum gas cost of 3,000,000 gas (we know this gas consumption because we have previously explored this approach).
- Secure: Whether it is the validity proof at the Layer 2 or at the Layer 1, it ultimately comes back to block proof, which is inevitably tied to on-chain data. Only with correct data can the block proof pass, and the final validity of the computation is verified within the zk-SNARK proof.
- Generalized: We support proofs for Ethereum, Arbitrum, Optimism, and zkSync Era. In the future, we plan to extend our support to more rollup networks. Additionally, we aim to allow third-party services to utilize our services.
Improvement points
- Timeliness: We do not perform real-time zk-SNARK proofs on on-chain data. Instead, we generate zk-SNARK proofs when a demand is initiated. Therefore, timeliness is crucial for us. Currently, our timeliness is influenced by two factors. First, the frequency at which various rollups update their corresponding state contracts on the Layer 1. Second, the complexity of zk calculations performed off-chain, where the time cost increases with the complexity. Presently, the time required for off-chain zk calculations and proof generation ranges from 2 to 4 hours(Test environment: 128GB RAM, 64 cores.). However, we are continuously working to optimize the time for circuit generation and proof generation. We are pursuing two approaches: optimizing the circuit itself and exploring hardware acceleration such as GPUs. Our goal is to achieve circuit proof generation within 10 minutes.
- Gas consumption: Currently, we use PLONK for recursive proof composition in Halo2. However, in order to reduce gas consumption for on-chain proofs, we are exploring the use of FFLONK for recursive proof composition in Halo2.
Introduction
The zk-SPV design we have developed aligns with the description provided in the earlier Yellow Paper: Zero Knowledge Simple Payment Verification. Prove the existence and rationality of Orbiter cross-rollup Tx through zero-knowledge proof technology. Existence means that both Source transaction and Destination transaction can be proved on L1 that they actually happened on the corresponding L2, and rationality refers to the ability to prove the user’s intention in SrcTx and ensure that the results of the payment made by the maker in DstTx comply with specific rules.
There are two types of rollups: optimistic rollups and zero-knowledge rollups. Their implementations are quite different, which also leads to the difference of the respective SPV implementations. The specifics of each Rollup’s SPV implementation will not be discussed in this context. Instead, we will utilize a standardized set of proof primitives to universally represent our SPV components. Reducing the gas consumption of transaction validity proofs by adopting zk-SNARK cryptographic technology.
Moreover, this document will solely focus on the technical implementation of SPV and will not involve any preconditions or postconditions.
Background
SPV: Simplified Payment Verification, firstly proposed in the BitCoin’s whitepaper. It allows a transaction recipient to prove that the sender has control of the source funds of the payment they are offering without downloading the full Blockchain, by utilising the properties of Merkle proofs.
Storage Trie: Storage trie is where all contract data lives. There is a separate storage trie for each account. To retrieve values at specific storage positions at a given address the storage address, integer position of the stored data in the storage, and the block ID are required.
Transactions Trie: There is a separate transactions trie for every block, again storing (key, value)pairs.A path here is: rlp(transactionIndex)
Receipts Trie: Every block has its own Receipts trie. A path here is: rlp(transactionIndex). transactionIndex is its index within the block it’s mined. The receipts trie is never updated. Similar to the Transactions trie, there are current and legacy receipts. To query a specific receipt in the Receipts trie, the index of the transaction in its block, the receipt payload and the transaction type are required. The Returned receipt can be of type Receipt which is defined as the concentenation of TransactionType and ReceiptPayload or it can be of type LegacyReceipt which is defined as rlp([status, cumulativeGasUsed, logsBloom, logs]).
Model
Logical model
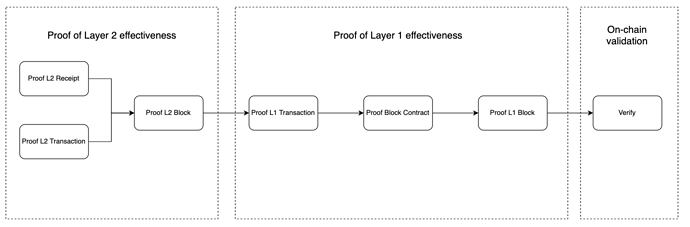
The entire proof process is divided into seven steps (referring to the longest steps to be taken during the proof).
- Proof of L2 receipt validity
- Proof of L2 transaction validity
- Proof of L2 block header validity
- Proof of L1 transaction validity
- Proof of L1 block contract state validity
- Proof of L1 block header validity
- On-chain contract verification
Among them, steps 1, 2, and 3 are referred to as Layer 2 validity proof, steps 4, 5, and 6 are referred to as Layer 1 validity proof, and step 7 is On-chain contract verification.
Therefore, the Complete proof of validity consists of Layer 2 validity proof + L1 layer validity proof.
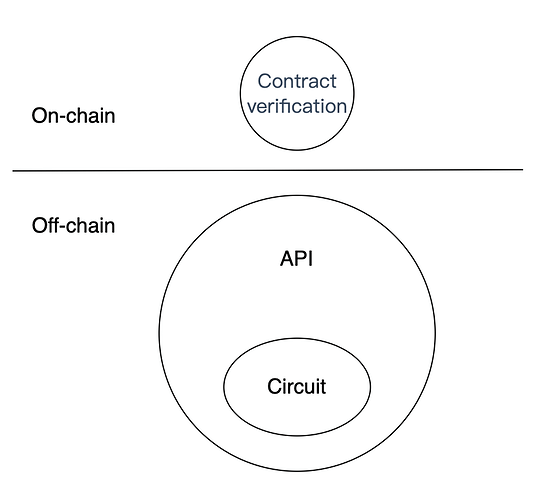
Physical model
- API: A set of off-chain RPC clients designed for SPV services. Externally, their function is to receive transaction and other information and generate zk-SNARK proofs of validity. Internally, they are responsible for constructing input data for circuits and persisting zk-SNARK proofs.
- Circuit: ZK circuits and libraries based on the Halo 2 proof system.
- Contract verification: On-chain verification contract for validating zk-SNARK proofs of validity.
Analysis
Scenario assumption
To provide a more accessible explanation focusing solely on how to achieve a complete proof of validity for an L2 transaction (i.e., the existence of the transaction, as described in the Yellow Paper), without delving into our specific business context:
Suppose we have an L2 transaction hash, denoted as H_{s}. We need to prove on the Layer 1 that H_{s} indeed occurred on L2 and was successfully executed. This proof is crucial for us to proceed with further business processing. However, we only possess the L2 transaction hash. How can we accomplish this?
Details
Proof of Layer 2 effectiveness
Proof of L2 receipt validity
Due to the one-to-one correspondence between the keys in the Receipts Trie and the keys in the Transactions Trie within the same block, the values with the same key represent the corresponding data of the same transaction. In other words, in Block B_{s} of the state root H_{s}, the transaction associated with H_{s} is denoted as T_{s}, and the receipt associated with H_{s} is denoted as R_{s}.
To prove H_{s}, we need to demonstrate whether H_{s} was executed successfully. The execution status of H_{s} can be determined by examining the Status field in the receipt of the transaction. Additionally, to prove the existence of R_{s} along a specific path in the Receipts Trie of B_{s}, an MPT (Merkle-Patricia Trie) is used. The specific path refers to the sequential order I_{s} of H_{s} within B_{s}. Furthermore, an API-generated Merkle proof denoted as M_{s} and the root hash of the Receipts Trie of B_{s}, denoted as MRH_{s}, are utilized. These data serve as inputs to the circuit and do not require any outputs or public inputs to be set.
Proof of L2 transaction validity
Certainly, we also need to utilize an MPT proof to demonstrate the existence of T_{s} along a specific path in the Transactions Trie of B_{s}. Moreover, we must provide the root hash of the Transactions Trie of B_{s}, denoted as MTH_{s}.
These data serve as inputs to the circuit, where T_{s} is considered a public input to facilitate subsequent on-chain verification.
Proof of L2 block header validity
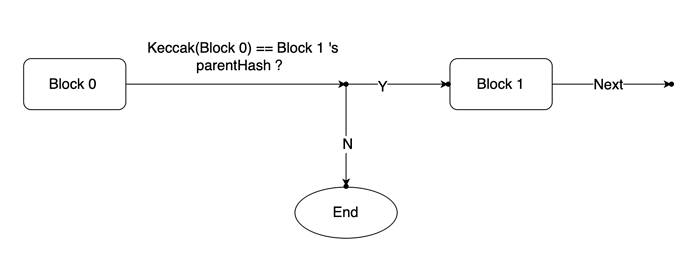
Next, this step requires proving that the progression from B_{s} to a specific trusted block is continuous. Blocks are strictly ordered, meaning that each newly created block contains a reference to its parent block. Consequently, each block includes the hash value of its parent block (ParentHash field), and the hash value of a block is generated by applying the Keccak hash function to its own RLP-encoded data.
Based on the L2 mechanism, it is certain that the Layer 1 always has corresponding state contracts to store specific states. Therefore, the trusted blocks originate from the on-chain contracts provided by official rollup implementations, such as Arbitrum’s Outbox contract, Optimism’s L2OutputOracle contract, zkSync’s Storage contract, and so on.
Thus, we can start from B_{s} and compute whether the previous block’s hash equals the parent hash value of the next block, continuously iterating until we reach the trusted block BT_{l2} (BT_{l2} \ge B_{s}).
These data serve as inputs to the circuit, where BT_{l2} is considered a public input for subsequent on-chain verification purposes.
Proof of Layer 1 effectiveness
Proof of L1 transaction validity
Even after H_{s} has undergone Layer 2 validity proof, is there any inherent connection between it and the Layer 1?
Every L2 transaction is packaged and submitted to the Layer 1 by the sequencer maintained by each rollup. The difference lies in the data recorded by the Layer 1, which represents different parts of the L2 transaction. For example, Arbitrum and Optimism record the compressed original data of L2 transactions (Arbitrum uses Brotli, Optimism uses Zlib), while zkSync Era records the state differences generated by all transactions within each batch.
Therefore, when H_{s} is packaged and submitted to the Layer 1 by the sequencer, the resulting transaction hash is H_{sub}, and the corresponding transaction is T_{sub}.
Next, it is necessary to prove that the L2 transaction (H_{s}) indeed exists within the submitted hash on the Layer 1. This means proving that the transaction information of H_{s} (which could be the transaction hash or the original transaction data) exists within the calldata of H_{sub}. We have already implemented decoders for Arbitrum and Optimism (for zkSync Era, we use nonce verification).
Of course, we also need to utilize an MPT proof to demonstrate the existence of T_{sub} along a specific path in the Transactions Trie of block B_{sub}, where the path refers to the sequential order I_{sub} of H_{sub} within B_{sub}. Additionally, we require the root hash of the Transactions Trie of B_{sub} (MTH_{sub}) and the merkle proof M_{sub}.
These data serve as inputs to the circuit and do not require any outputs or public inputs to be set.
Proof of L1 block header validity
Similarly, after performing transaction validity proof on the Layer 1, we also need to prove the continuity from B_{sub} to a specific trusted block BT_{l1} (BT_{l1} \ge B_{sub}).
To reduce the time cost of off-chain computation and enhance on-chain operability, we have an L1StorageBlockHash contract. Ideally, this contract records the latest block hash of the Layer 1 at an hourly interval, storing it in the form of bytes32->uint256 mapping. The contract has no permissions and anyone can update the block hash. Currently, it is maintained by our official team, but there are plans to incentivize others to participate in updating the state. Since these block hashes are directly read from the contract using blockhash(), they can be considered valid. (We did consider using a Merkle tree, but it didn’t align well with our business requirements.)
These data serve as inputs to the circuit, where BT_{l1} is considered a public input for subsequent on-chain verification purposes.
Proof of L1 block contract state validity
This section is described at the end because it is optional in the proof process.
Smart contracts store data in the long-term memory of the blockchain, with a memory layout represented as a mapping of uint256 -> uint256. This layout is known as storage slots. By accessing storage slots, we can retrieve the values stored within. As long as we accurately know the memory layout of a specific contract and can calculate the storage slot key, it becomes straightforward to prove the contract’s state. (That is, proving the value of a specific state variable for a particular contract in a specific block)
Additionally, we need to perform a Proof of L1 block header validity, linking the block hash to the trusted block (sourced from the L1StorageBlockHash contract).
As the scenario assumption does not include contract state proofs, here is a brief summary of the circuit for contract state proofs:
Let A represent the address of the contract to be proved. The storage slot key to be proven is denoted as S_{k} (which can be manually calculated or computed using our provided shortcut tool, which is being gradually improved). The value of the storage slot to be proved is denoted as S_{v}. The block hash or block number to be proven is denoted as B_{a}, and the trusted block is denoted as BT_{a} (BT_{a} \ge B_{a}).
These data serve as inputs to the circuit, where S_{k}, S_{v}, B_{a}, and BT_{a} are considered public inputs for subsequent on-chain verification purposes.
On-chain contract verification
Upon completing the aforementioned steps, a zk-SNARK proof of validity, denoted as P_{zk}, is generated. Simultaneously, the public inputs or outputs from the aforementioned steps (if defined) are passed to the verification contract for on-chain validation. Once the validation is successful, it confirms the occurrence and successful execution of H_{s} on the Layer 2, as proven on the Layer 1. The final result (public inputs or outputs) can be securely utilized in your smart contract without the need for trust.
Our Project Engineering Code
Those who are interested can visit our github library.