Inactivity Leak unveiled

ulrych8 · June 10, 2024, 1:46pm

We summarize here the article that presents the first theoretical analysis of the inactivity leak, designed to restore finalization during catastrophic network failures. This work is accepted at DSN2024.

TL;DR

The inactivity leak is intrinsically problematic for the safety of the protocol. It favors the constant finalization of blocks (liveness) at the expense of having conflicting finalized blocks (safety).
The presence of Byzantine validators -validators that deviate from the protocol- can accelerate the loss of safety.

The Ethereum PoS blockchain strives for the continuous growth of the finalized chain. In consequence, the protocol incentivizes validators to finalize blocks actively. The inactivity leak is the mechanism used to regain finality. Specifically, the inactivity leak is initiated if a chain has not undergone finalization for four consecutive epochs. The inactivity leak happened for the first time on the mainnet in May 2023.

A good introduction to the inactivity leak is available thanks to the excellent work of Ben Eddington here (which motivated this work). We formalize the inactivity leak starting by the inactivity score.

Inactivity Score

During an inactivity leak, at epoch t, the inactivity score, I_i(t), of validator i is:

\begin{cases} I_i(t) = I_i(t-1)+4, \text{if $i$ is inactive at epoch $t$} \\ I_i(t) = \max(I_i(t-1)-1, 0), \text{ otherwise.} \end{cases}

Thus, a validator’s inactivity score increases by 4 if it is inactive and decreases by 1 if it is active. The inactivity score is always positive and will be used to penalize validators during the inactivity leak.

Inactivity Penalties

Let s_i(t) represent the stake of validator i at epoch t, and let I_i(t) denote its inactivity score. The penalty at each epoch t is I_i(t-1)\cdot s_i(t-1)/2^{26}. Therefore, the evolution of the stake is expressed by:

s_i(t)=s_i(t-1)-\frac{I_i(t-1)\cdot s_i(t-1)}{2^{26}}.

Stake during the Inactivity Leak

In this work, we model the stake function s as a continuous and differentiable function, yielding the following differential equation:

s'(t)=-I(t)\cdot s(t)/2^{26}.

With this equation, we can determine a validator’s stake according to the time by fixing the evolution of its inactivity score. And that is exactly what we do. We define two types of behavior: Active and Inactive.

Active validators: they are always active.
Inactive validators: they are always inactive.

Validators with these behaviors experience different evolutions in their inactivity scores: (a) Active validators have a constant inactivity score I(t)=0; (b) Inactive validators’ inactivity score increases by 4 every epoch, I(t)=4t. The stake of each type of validator during an inactivity leak:

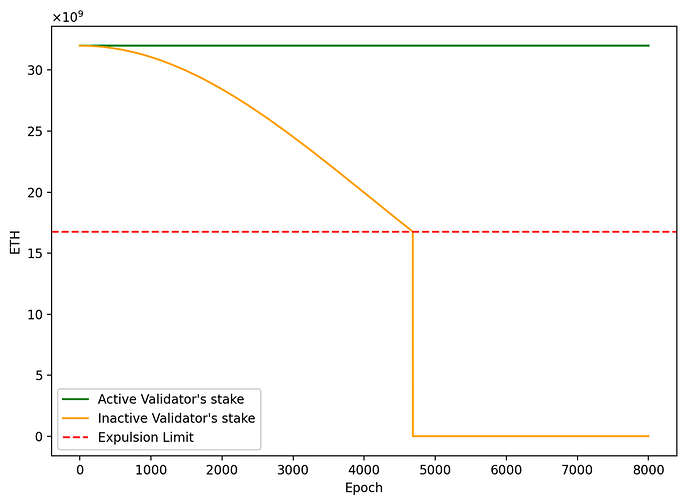
Active validator’s stake: s(t) = s_0 = 32.
Inactive validator’s stake: s(t) = s_0e^{-t^2/2^{25}}.

The graph shows the evolution of the stake of validators depending on their activity during the inactivity leak. The expulsion limit is set by the protocol to eject validators that have accumulated too many penalties.

What is an active validator?

This is an important detail; the activity is actually chain-dependent. This means that different chains will have different inactivity scores for the same validator. Hence, a validator can be ejected from a chain and not lose a wei on the other chain.

This was the formalization of the protocol. Now we make the analysis of the protocol’s property of safety. To do so, we use the following model.

Model

Network: We assume a partially synchronous system, which transitions from an asynchronous state to a synchronous state after an apriori unknown Global Stabilization Time (GST).
Fault: Validators are either honest or Byzantine (deviating from the protocol). A Byzantine validator can deviate arbitrarily from the protocol.
Stake: Each validator starts with 32 ETH.

There is no bound on message transfer delay during the asynchronous state.

Bound for safety

With only honest validators

By construction, the inactivity leak will breach safety if a partition occurs for long enough. The question is, how quickly?

Any network partition lasting longer than 4686 epochs (about 3 weeks) will result in a loss of Safety because of conflicting finalization. This is an upper bound for Safety on the duration of the inactivity leak with only honest validators.

Detailed Analysis

Let us analyze the scenario in which the validators (which are all honest) are partitioned in two. (We are in the asynchronous state according to our model).
The partition will necessarily create a fork, each partition building on the only chain they see. The chains will finalize once the proportion of active validators returns to 2/3rd.

In this case, by understanding the distribution of the validators across the partitions, we can compute the time it takes for the proportion of active validators’ stake to return to 2/3 of the stake on each branch, thus finalizing and breaking safety.

For the analysis, we make the following notations. At the beginning of the inactivity leak:

n is the total number of validators
n_B is the total number of Byzantine validators
n_H is the total number of honest validators
n_{H_1} is the number of honest validators on branch 1
n_{H_2} is the number of honest validators on branch 2

There are no Byzantine validators for the first part of our analysis, which implies that n=n_H. Honest validators are only partitioned in two, thus n_H=n_{H_1}+n_{H_2}.

Our goal is to determine when the proportion of honest validators on branch 1 will be superior to 2/3rd of the total stake. Which is to say that we look at when the ratio:

\frac{\text{stake of validator in branch 1}}{\text{stake of validator in branch 1 + stake of validator in branch 2}},

is superior to 2/3. With our notation, the ratio can be rewritten as:

\frac{n_{\text H_1}s_{\text H_1}(t)}{n_{\text H_1}s_{\text H_1}(t)+n_{\text H_2}s_{\text H_2}(t)} ,

s_{\text H_1} and s_{\text H_2} are the stakes of honest active and inactive validators, respectively. Since the n_{\text H_1} validators on branch 1 are always active on branch 1, and the n_{\text H_2} validators are always inactive on branch 1 (they are active on branch 2); we know that s_{\text H_1}(t)=s_0 and s_{\text H_2}(t)=s_0e^{-t^2/2^{25}}.
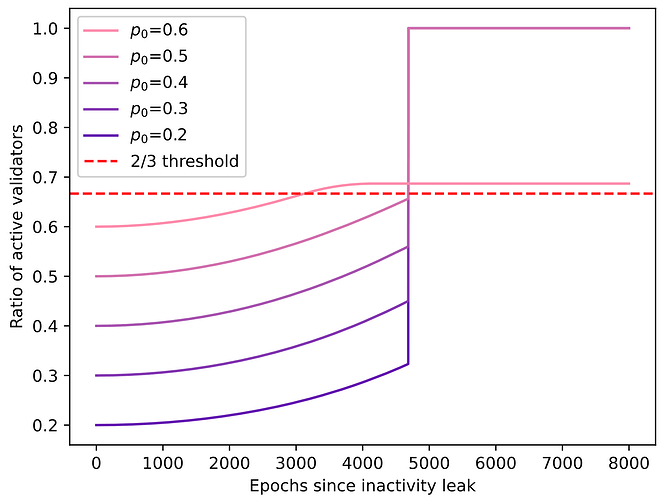
Using the notation p_0=n_{\text H_1}/n_H, the ratio of active validators over time is:

\frac{p_0}{p_0+(1-p_0)e^{-t^2/2^{25}}}.

This graph shows the ratio of active validators on branch 1 over time. If finalization hasn’t occurred by epoch t=4685, inactive validators are ejected, causing a jump to 100% active validators.

Byzantine validators

We now add Byzantine validators.

These Byzantine validators can send messages to each partition without restriction.

This might seem like excessive power, but this is a traditional assumption in distributed systems to give Byzantine even more power. The Gasper paper which present the ETH2 protocol, mention extensively the PBFT paper in their model. Here is a sentence of the PBFT paper: “We allow for a very strong adversary that can coordinate faulty nodes, delay communication, or delay correct nodes in order to cause the most damage to the replicated service.”
Our assumption is less strong. Imagine the case of a partition where the communication between Europe and America is severed, but the communication inside each region still works. According to our model, we assume Byzantine validators could communicate with both regions without restriction as if they had their own way of communicating across regions.

The situation we analyze is now as such:

Less than one-third of the stake is held by Byzantine validators (\beta_0=n_{\rm B}/n<1/3).
Honest validators are divided into branches 1 and 2; a proportion p_0=n_{\rm H_1}/n_{\rm H} on branch 1 and 1-p_0=n_{\rm H_2}/n_{\rm H} on branch 2.
Byzantine validators can communicate with both branches.

Byzantine validators can be active on both branches simultaneously, breaching safety faster. The ratio of active validators on branch 1 is:

\frac{p_0(1-\beta_0)+\beta_0}{p_0(1-\beta_0)+\beta_0+(1-p_0)(1-\beta_0)e^{-t^2/2^{25}}}.

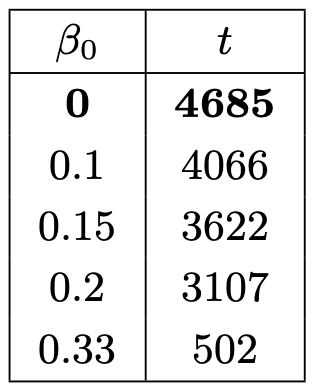
This table shows the time it takes to break safety depending on the initial proportion of Byzantine validators (\beta_0):

Byzantine validators can expedite the loss of Safety. If their initial proportion is 0.33, they can make conflicting finalization occur approximately ten times faster than scenarios involving only honest participants.

The original paper provides more details on the assumptions, scenarios, protocol, and other aspects such as:

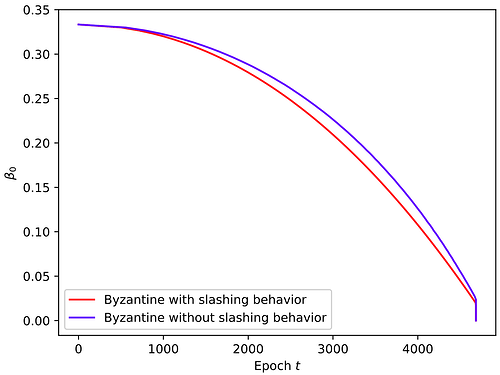
Ways for Byzantine validators to breach safety without committing slashable behavior.
Methods for Byzantine validators to exceed the 1/3 threshold on both branches of the fork.
An analysis of the probabilistic bouncing attack while considering the inactivity leak. Spoiler alert: this aggravates the attack slightly, but the conditions for the attack to start and persist in time make it highly improbable to be a real threat.

For an additional quick peek at the paper’s findings, here is a graphic that presents how quickly Byzantine validators can break safety depending on their initial proportion and whether their behavior is slashable or not. As you can see, they can have a strong impact even without slashable behavior.

Conclusion

Our findings highlight the importance of penalty mechanisms in Byzantine Fault Tolerance (BFT) analysis. By identifying potential issues in protocol design, we aim to provide insights for future improvements and tools for further investigation.