In this article, we propose a way that could significantly increase a PoW blockchain double-spending attacking cost (potentially different orders) with staking (and slashing of course).
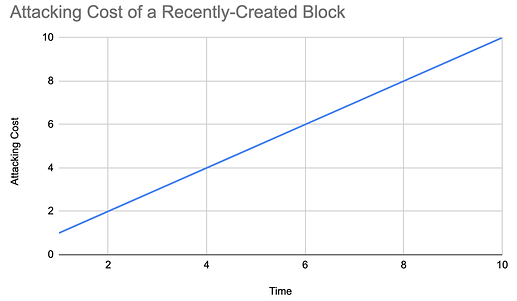
Definition 1 (Attacking Cost of A PoW Chain): Given chained blocks \mathbf{B} = [B_0, B_1, ..., B_l] of a PoW chain, the attacking cost of reverting a recently-created block B_i by creating an attacking fork is about
C(B_i) \approx \sum_{j=i}^{l} D(B_j) \approx \int_{T(B_i)}^{now} H(t)dt \approx H \times (now - T(B_i))
where D(B_j) returns the cost of creating a block with the same difficulty of B_j, T(B_i) is the block creation time, H(t) is the cost of the network hash rate at time t, and H(t) = H is almost-constant from now to T(B_i).
Now we impose a staking constraint for a PoW block:
Definition 2 (A PoW Chain with Staking): To produce a block, besides reaching the block difficulty, a miner must stake S(N + 1) tokens, where S is a pre-defined token numbers, N is the number of blocked mined by the same miner in recent W blocks. Note that the staked tokens will be locked much longer than the production time of W blocks to prevent transfer-and-stake cheat.
With the definition, we now have the following proposition
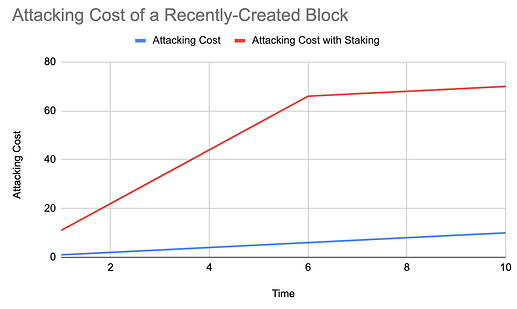
Proposition 1(Attacking Cost of A PoW Chain With Staking) The attacking cost of reverting a recently-created block B_i, i > l - W by creating an attacking fork is
\bar{C}(B_i) \approx \sum_{j=i}^{l} (D(B_j) + S (l - i + 1)) \approx \int_{T(B_i)}^{now} (\bar{H}(t) + S P / T)dt \approx (\bar{H} + S/T) \times (now - T(B_i)), and P is the token price.
where \bar{H}(t)=\bar{H} is the post-stake network hash rate cost, and S (l - i + 1) are the number of tokens of the attacker that are slashed after the attack is discovered.
Example: Using Ethereum as exapmle, suppose W = 1000, S = 200, T = 15, and price per ETH is P = 180 USD, the attacking cost of reverting a blocked generated 5 mins ago (about 20 block confirmations) with staking will be about 20 \times S \times P = 20 \times 200 \times 180 = 720,000 USD, while the upper limit of attacking cost without staking is about 2 \times 20 \times P = 7,200 USD. Note that, all miners require to stake 1000 \times 200 = 200K ETH to prevent the network staling.