Initial explorations on full PoS proposal mechanisms

Proof-of-Stake
1

Hybrid Casper FFG uses proof of stake to finalize blocks, but still leaves to proof of work the responsibility of proposing them. To reach full PoS, the task is thus to come up with a proof of stake block proposer.

Here is a simple one, and the one that is currently used for the sharding validator manager contract:

  • All validators have the same deposit size
  • Suppose there are N active validators. Take some source of randomness, R; compute R % N, and take the validator at that index as the next validator.

This has the benefit of being extremely concise to implement and reason about, but has several flaws:

  • If a validator gets the ability to propose a block, not only the validator but also everyone else will know ahead of time
  • It does not support variable validator sizes
  • In the case of Casper FFG, if it is intended for blocks to double as votes, then it’s ideal to have all validators appear within each epoch, ideally in a permutation without repetitions, so that finalization can happen

The first problem is out of scope of this post (see here for an ingenious solution using linkable ring signatures). To solve the second problem in isolation, the main challenge is developing a random sampling algorithm where each validator has a probability of being selected proportional to their deposit balance. This can be solved using a binary tree structure, as implemented here. This has O(log(n)) overhead, but the largest overhead only arises when balances are changed or validators are inducted or removed; simple random selection only takes O(log(n)) SLOAD calls, so <5000 gas.

For the third problem, the easiest solution is to set the epoch length to equal the number of active validators, and select a permutation at the start of the epoch. If there are N validators, this may be done by randomly selecting a P coprime to N (that is, something like P = sha3(R) % N; while gcd(P, N) != 1: P += 1), and then cycling through (i * P) % N for all 0 <= i < N. One can also use Las Vegas algorithms (keep randomly picking validators until you find one that has not already been used in the current period); this reduces “lookahead transparency” at the cost of adding a bit more complexity and runtime.

Solving the second and third at the same time, however, is more challenging. There is a conflict between:

  1. The needs of the consensus algorithm, which requires (almost) every validator to “speak up” at least once per period
  2. The goal of fairness, which requires the expected number of blocks created by a validator to be proportional to their deposit size
  3. The goal of shortening period length to reduce time-to-finality.

Optimally reconciling (1) and (3) requires each validator to have exactly one slot, but this contradicts fairness.

One can combine (1) and (2) with a hybrid algorithm; for example, one can imagine an algorithm that normally just randomly selects validators, but if it notices that there are too many not-yet-selected validators compared to the number of blocks left in the period it continues looking until it finds a not-yet-selected validator. Alternatively, one could use the (i * P) % N round robin interspersed with a random algorithm where the probability of getting selected is proportional to balance - min_balance. In all cases, the expected period length is total_balance / min_balance. If we assume account balances are distributed according to Zipf’s law, that’s roughly N * log(N).

One can achieve an even better result with an exponential backoff scheme: use any form of randomness to select validators, then start the epoch length at some very small number. Chances are, the first epoch will be so small that only a small percentage of validators will be able to participate, and so hitting the 2/3 threshold is impossible. However, every time we fail to come to consensus, we simply double the epoch length until eventually we get to 2/3. This mechanism has the advantage that it does not rely on a high min_balance; if there is a large number of very-small-balance validators but they only make up a small portion of the total deposit, most of the time the larger validators will be able to finalize by themselves.

Currently, I favor this latter scheme.

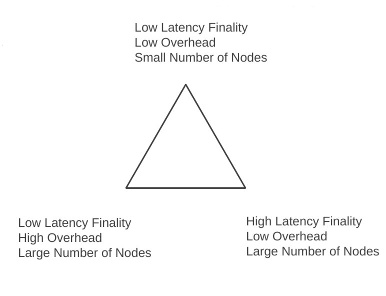
The other important topic that needs to be covered is parametrizing the overhead / finality time / node count tradeoff. See also Vlad’s expression in triangle form:

DROeWQSXcAEbdzu

Mathematically speaking, it’s the result of a simple inequality:

overhead \ge \frac{2 * NumValidators}{TimeToFinality}

Achieving finality requires two messages from every validator that must be processed by the blockchain, so the rest follows trivially. There are two ends of the tradeoff that are obvious:

  1. PBFT et al: every node sends a “vote” every block, so low time to finality, hence low node count or high overhead
  2. Chain-based: votes are blocks, so same low overhead and high node count potential as any other chain-based algo, but high time to finality

I believe that the optimal solution lies in the middle. Casper FFG already does this, supporting:

  • A medium amount of nodes (1000-3000, not an unlimited amount like “naive PoS” chains bit also not ~20-30 like many DPOS chains)
  • A medium time to finality (not 5s, but also not “never” like naive PoS chains) and a medium
  • A medium amount of overhead (~1-2 messages per second, not ~0.07 per sec like the current ethereum chain but also not tens or hundreds per second like many DPOS chains)

But with full proof of stake, there is a binary divide: either votes are blocks, in which case you go full chain-based, or votes are not blocks, in which case you have a redundancy between the two, with the protocol having to handle the overhead of both. One could simply accept the redundancy, accepting how Casper FFG works, but then adding in a PoS block proposer, but we may be able to do better. If we are okay with having 1-2 messages per second of consensus overhead, then we can have these consensus messages contain references to a small list of transactions, and use fancy directed acyclic graph techniques to gather these transactions into a history, ensuring convergence happens as quickly as possible (insert coindesk article and reddit posts saying “Ethereum foundation is exploring hashgraph/DAG technology!!!1!!” here).

There are two other possibilities:

  1. With sharding, Casper votes can also serve double-duty as collation headers. Because there are 100 shards, with a block time of ~75 seconds (period length 5 blocks) on each shard, the total overhead of the system just happens to also be ~1-2 messages per second.
  2. When a block is created, a random set of N validators is selected that must validate that block for it to be possible to build another block on top of that block. At least M of those N must sign off. This is basically proof of activity except with both layers being proof of stake; it brings the practical benefit that a single block gives a very solid degree of confirmation - arguably the next best thing to finality - without adding much complexity. This could be seen as bringing together the best of both worlds between committee algorithms and full-validator-set algorithms.

Currently, I favor (2).

7 Likes
2

I believe that the ring signature scheme achieves this. The sampling is a permutation without repetitions. I call it “perfect fairness” in the original post.

Regarding deposit sizes, my latest (not too strongly held) opinion is that fixed-size deposits beat variable-size deposits:

  • Granularity: Multiple fixed-size validators can be ultimately controlled by the same entity. So from the point of view of the freedom to choose the deposit amount, fixed-size deposits allow for variable-size deposits, just with less granularity. For large deposits the added value of greater granularity dies off quickly, and for small deposits the added value is limited by the minimum deposit size.
  • Decentralisation: By breaking down large validators into smaller equally sized sub-validators we can increase decentralisation and improve incentive alignment. The reason is we can use cryptographic techniques to force a fixed amount of non-outsourceable non-reusable work per identity. (For example, we may be able to enforce proof-of-storage per identity, or maybe proof-of-work per identity using a proof of sequential work, or maybe proof of custody can help with outsourceability.) I believe the dfinity project is partly taking the fixed-size deposit approach for this reason. One could try to argue that variable-size deposits are good because they allow for batching and pooling, reducing node count, hence reducing overheads at the consensus layer. The potential problem is incentive misalignment, whereby the cost of validation grows “sublinearly” with deposit size.

So all in all I think the ring signature scheme has the right properties: perfect privacy (going beyond private lookahead with private lookbehind), fixed-size deposits, and perfect fairness.

2 Likes
3

Hello,

I agree with the concept.

For solving the second and third points, a logarithmic function would be useful :

Let’s take a realistic example :

  • 2 000 small validators staking a minimum of 1 000 eth = 2 000 000 eth

  • 1 000 middle validators staking an average of 10 000 eth = 10 000 000 eth

  • 100 big validators staking an average of 100 000 eth = 10 000 000 eth

  • 5 very big validators staking an average of 1 000 000 eth = 5 000 000 eth

Total number of validators : 2 000 + 1 000 + 100 + 5 = 3 105 (it’s pretty realistic : today, Dash runs swiftly with more than 4 700 masternodes, Zcoin with 2 000 and Sibcoin with 8 000)

Total ethereums staked : 2 000 000 + 10 000 000 + 10 000 000 + 5 000 000 = 27 millions

Next step, let’s implement a logarithmic function f_log giving a value of 1 for small validators with 1 000 eth.

  • f_log (small validator) = f_log (1 000 eth) = 1 (for all 2 000 small validators, the sum of f_log would then be 1 x 2 000 = 2 000)

  • f_log (middle validator) = f_log (10 000 eth) = 2 (for all 1 000 middle validators, the sum of f_log is 2 x 1 000 = 2 000)

  • f_log (big validator) = f_log (100 000 eth) = 3 (for all 100 big validators, the sum of f_log would be 3 x 100 = 300)

  • f_log (very big validator) = f_log (1 000 000 eth) = 4 (for all 5 very big validators, the sum of f_log would be 4 x 5 = 20)

Sum of logarithmic function of all validators : 2 000 + 2000 + 300 + 20 = 4 320.

So if you take a period of time of 4 320, and if the probability of being chosen as validator to build the block is proportional to the f_log function of stake, then, during this period :

  • each small validator will on average propose 1 block (and could be rewarded based on his stake of 1 000)

  • each middle validator will on average propose 2 blocks (and could be rewarded based on his stake of 10 000)

  • each big validator will on average propose 3 blocks (and could be rewarded based on his stake of 100 000)

  • each very big validator will on average propose 4 blocks (and could be rewarded based on his stake of 1 000 000)

This period of 4 320 is only a little bit more than the number of validators (3 105), so the logarithmic function is very efficient here, not to make the full period too long.

If you take a period of 6 000 or 7 000 , then there is a high probability the vast majority of validators will create at least a block.

There’s no need that absolutely every validator creates a block in every period. But on average they will.

Concerning the other topic, I agree with a balance between a medium amount of nodes, a medium time to finality and a medium amount of overhead.

The last topic is rather optimization and could be implemented later.

I think the first implementation of full POS should be as simple as possible to see how the network will react : when a block is proposed by the chosen online validator, other validators could just validate the block progressively. It would be like in bitcoin validation, when you see the number of confirmations growing over time. With POS, it would just be much faster.

1 Like
4

The problem with fixed size deposits is simple efficiency: they require a large validator to sign many times, whereas with variable size deposits the large validator only needs to sign once. If you assume validators are distributed according to Zipf’s law, that’s a log(n) factor difference. Estimates from here suggest a ~8x concrete efficiency gain from variable size deposits. Of course, this is nullified if you are using a scheme that requires large validators to create multiple blocks, but as I mention we don’t necessarily need that.

I believe that the ring signature scheme achieves this. The sampling is a permutation without repetitions. I call it “perfect fairness” in the original post.

Ah, I see, you mention:

To remove any time-based correlation across logs, we publicly shuffle the array using public entropy.

Algorithms like the i * P % N I mention above would be examples of how to publicly shuffle.

1 Like
5

To achieve that validators worth at least 2/3 of total deposits get a block in a epoch, you could sample Las Vegas style until you reach 2/3 of deposits and after that draw normally for the rest of the epoch.

To achieve this over the long run, you could keep track of chance balances per validator.
At the beginning of each epoch (of N blocks) you add the deposit amount of the validator to the chance balance. You draw the validators relative to the size in the chance balance. For every time a validator is chosen you subtract total_balance/N from the chance balance.
If a validators chance balance is negative, this validator can not be chosen and has to wait for it to turn positive again. If after an epoch a validators chance balance is still positive, this balance is carried over to the next epoch in increase its chances.

You can choose the length of the period such that you have a > 99% chance of reaching the 2/3 of total deposits in each epoch (using the Las Vegas sampling). This off course depends on the distribution of the deposits. The more evenly distributed, the more blocks we need.

6

Selecting can be made O(1) for variable deposits.

  1. array with (address : balance+sumOfPreviousBalances) sorted by the second field (let’s call it summedEth).
  2. R - random number between 0 and sum of all stake, based on previous block(s)
  3. the next validator is the one whose summed balance contains R.

Computation is done off chain. The next validator posts proof along with his vote - array index. On-chain it’s only checked that

(R >= validatorTable[i].summedEth) && (i == validatorCount-1 || R < validatorTable[i+1].summedEth)

Btw, 64 bytes for (address : wei) pair seems wasteful. With balance precision reduced by 2 bits 32 bytes would be enough for address (20 bytes) : weis/4 (12 bytes) which allows for 316B eth.

1 Like
7

Here’s a variant of the ring signature scheme to capture the efficiency gains of a Zipfian distribution. Start off by only allowing a few hand-picked deposit sizes that best “fit” the expected distribution to reduce node count. For example the only allowable deposit values could be 1K, 5K, 25K and 125K ETH. Then when a proposal is made, augment the signature by the ephemeral identity with a zk-proof for the deposit amount.

In a scheme with perfect fairness notice that private lookbehind is necessary for private lookahead. The reason is that if non-ephemeral identities are leaked at the time of proposal, then by means of elimination the private lookahead breaks down as the epoch progresses because of the “rigidity” of perfect fairness.

The above scheme achieves a nice efficiency gain, and only slight compromises on private lookbehind:

  • only deposit amounts are disclosed (not the non-ephemeral identities)
  • deposit amounts are heavily restricted, so validators will form groups with equal deposit amounts, leading to a high degree of privacy
1 Like
8

This doesn’t work because it would take O(N) time to update. You could store sumOfPreviousBalances in a more fancy data structure, but that makes everything O(log(n)) and is basically my solution.

Here’s a variant of the ring signature scheme to capture the efficiency gains of a Zipfian distribution. Start off by only allowing a few hand-picked deposit sizes that best “fit” the expected distribution to reduce node count. For example the only allowable deposit values could be 1K, 5K, 25K and 125K ETH. Then when a proposal is made, augment the signature by the ephemeral identity with a zk-proof for the deposit amount.

OK, fair :slight_smile:

And I did the math and that seems to actually average O(1) per user even with Zipf’s law, though with a higher constant factor.

1 Like
9

Cool :slight_smile:

Out of curiosity could you share the math? What constant did you get?

10

Here’s the approximation:

\sum_{k=1}^n 1 + log(\frac{n}{k}) = \sum_{k=1}^n 1 + log(n) - log(k) = n + n*log(n) - (n*log(n) - n) = 2n

The first expression is the sum over all validators of the number of slots that the validator would need to have, which is roughly 1 + log(x) if it has a size x.

This is subtracting approximations from each other in a way that can easily lead to destructive error amplification so I would not trust the specific number too much though.

11

For small clusters IMHO the best algorithms (and the hardest to implement) are fully asynchronous master-less timeout-less “atomic broadcast” protocols such as this

A positive thing about these algorithms is that a single bad node can not slow down the system since there is no master and no timeout. In fact, in a cluster of good nodes, the slowest 1/3 nodes do not pay much role, since atomic broadcast protocols typically wait for 2/3 nodes to respond.

A problem with atomic broadcast algorithms is that the best of them scale as N^2 in message complexity. Because of this, large clusters are not really practical.

We are working on a project for something that we call a “Map-Reduce” parallel consensus. It aims to overcome the scaling problem by running multiple instances of consensus on each subgroup of nodes.

Essentially, instead of having one instance of atomic broadcast consensus, one has multiple parallel consensus instances in a “fractal” fashion. As an example, if you have a cluster of a 256 nodes, you split it into 16 groups of 16 nodes, and then run 16 instances of asynchronous consensus in parallel, one consensus instance for each group. Then you get 16 small blocks, that you provide as inputs for higher level consensus. You then run a high level instance consensus to order these block and create one large block. In this way, we believe we can get to fast finality even for larger chains, as the finality time will be essentially proportional to a logarithm of the chain size. In addition, consensus becomes really a parallel thing where different subgroups of nodes work different sub-tasks in parallel.

It is a research project at the moment, I will post more on the as we are test the idea …

12

I actually dislike these for cryptoeconomic reasons: if you have a leader, then incentives are well-aligned in that you know exactly what the leader’s incentives are in transaction fee ordering, you can bribe them by paying a higher fee, and everyone knows how this is works. When there are N parties sharing the responsibility in some way where each one only has small influence over the outcome, then it gets weirder.

13

I agree that fully asynchronous protocols may be a bit more difficult to debug and if something goes wrong attribution of wrongdoing is not easy … (on the other hand it is harder for things to go wrong in fully asynchronous protocols, since failure of a small portion of nodes does not affect things much …)

If you like PBFT, could you still do parallel processing by running multiple PBFT instances to create small blocks, and feed the resulting small blocks into a higher level PBFT instance to order them into the final block ? This could be a way to reduce overhead of running PBFT on a large chain, having that PBFT scales as N^2 …

14

I’m not sure how \sum_{k=1}^n 1 + log(n) - log(k) = n + n*log(n) - (n*log(n) - n), could you spell it out? I thought \sum_{k=1}^n 1 + log(n) - log(k) = 1 + log(n) - log(k) .

1 Like
15

\sum_{k=1}^n 1 + log(\frac{n}{k})
= \sum_{k=1}^n (1 + log(n) - log(k))
= \sum_{k=1}^n 1 + \sum_{k=1}^n log(n) - \sum_{k=1}^n log(k)
= n + n*log(n) - (n*log(n) - n)
= 2n

The only nontrivial part in there is \sum_{k=1}^n log(k) \approx n*log(n) - n

1 Like
16

image
image991Ă—57 5.66 KB

1 Like
17

So the next order term is log (n) / 2, but it does not matter for large n :slight_smile:

1 Like
18

Ah, I thought the parentheses might have been missing but it’s good that you added them to clarify.

\sum_{k=1}^n \log(k) = \int_{k=1}^n \log(x) \, dx+ \frac{\log(n)}2 + \frac{\frac 1n - 1}{12} - \frac 1{30}\frac{-\frac 1{n^2} +1}{4!}+\cdots +B_{2k}\frac {f^{(2k-1)}(n)-f^{(2k-1)}(m)}{(2k)!}+R_{2k}
= n\log(n) - n + \frac{\log(n)}2 + \frac{\frac 1n - 1}{12} - \frac 1{30}\frac{-\frac 1{n^2} +1}{4!}+\cdots +B_{2k}\frac {f^{(2k-1)}(n)-f^{(2k-1)}(m)}{(2k)!}+R_{2k}
=\lim_{x\to \infty} (n\log(n) - n)

For the non-trivial part, I spent a few hours reading and think I get the gist of it.

1 Like
19

Selecting can be made O(1) for variable deposits.

array with (address : balance+sumOfPreviousBalances) sorted by the second field (let’s call it summedEth).
R - random number between 0 and sum of all stake, based on previous block(s)
the next validator is the one whose summed balance contains R.

This doesn’t work because it would take O(N) time to update. You could store sumOfPreviousBalances in a more fancy data structure, but that makes everything O(log(n)) and is basically my solution.

Some of the techniques in this thread seem overengineered/prematurely optimized. The proposed minimum stake is quite high, meaning the N (number of validators) won’t be large - does the difference between O(N) and O(log(N)) here actually matter? We know simplicity matters.

How beneficial is it really, even for FFG, “to have all validators appear within each epoch”? I suspect random selection wouldn’t greatly slow down finalization times (2/3 support). Also, wouldn’t permutation let one predict which validators got their turn late in the round - the ones who didn’t go early? Mightn’t that invite vulnerabilities? PoW makes no guarantees whatsoever in the short term (eg, large BTC miners sometimes don’t earn a block all day due to bad luck), and this has caused strikingly few problems. And ETH’s much shorter block times provide a lot more statistical smoothness anyway.

@nootropicat’s O(N) “R % N weighted by stake” approach seems intuitive and fit-to-task to me. What specific practical problems would it cause?

Also, how reliable (unpredictable) are ETH’s internal sources of randomness so far? Most/all of these proposal mechanisms depend on one, and that seems like a highly practical attack vector to defend against.

1 Like