Is this really a Binomial distribution?-I believe the formula is not accurate

Sharded Execution
1

Regarding the article

I have some doubts about the formula in here

Screenshot_2021-07-20-22-20-19-75
Screenshot_2021-07-20-22-20-19-75720×1600 125 KB

-First of all, the formula presented is missing a parameter say “M” to represent the number of groups ( committees we have), where the probability P of myopic represents having say “X” malicious such that
P=X/NM
So there must be something wrong in this formula

-True at the end the shuffling algorithm chooses one at random, this could mean to divide the resulting probability by 1/M, but not to execlude M at all; I don’t think things are that simple.

-Bernoulli trials ( which the binomial distribution is based on) only have two outcomes ( like throwing a coin), but we here have more than 2 groups; it looks like the number of slots was mixed up with the number of groups or maybe the simple example above it.
-It could be more viewed like throwing a dice only with M outcomes (I mean throwing a dice is a special case or example with M=6)
»»»I think there maybe(probably) a known formula or distribution for such probability that I can’t recall now
.
-Another way of viewing it is like u have an NM bits number where u know have exactly X=PN*M 1s (or 0s), we want to know the probability that when partitioning the number to groups of N contiguous bits, at least N/2 of the X 1s will be in one of those groups.

Till we are able to derive a general formula ( or someone remind us of known one from the literature), please follow this simple examples with me to realize the error in the equation when we have more than 2 groups; ie. M≥3
.
-Let M=3, N=5 (15 attestor divided into 3 groups of 5 each)
-say X=4 ( we have 4 malicious/myopic persons) where 0.25≤(P=4/15)≤0.33
P~=0.2666…
.
The 4 malicious (consider them persons, ie identity matters let’s call them A,B,C,D)
Have 3⁴=81 ways to be distributed over the 3 groups (each has 3 choices to one of the groups, and in general these choices are indep as long as N≥X)

-Possible outcomes are:

4,0,0 ==⟩ can happen in 3 ways
(which of the 3 groups they will be in)

3,1,0 ==⟩ can happen in 432=24 ways:
Pick each of the 4 be the single one and choose its group in 3 different ways, the remaining have 2 choices of the 2 remaining groups; in detail
ABC,D,0/ABC,0,D/0,ABC,D/0,D,ABC/D,ABC,0/
D,0,ABC
Then repeat for
ABD,C,0
BCD,A,0
ACD,B,0
.
Till now prob =(3+24)/81=27/81=1/3
That’s larger than initial probability (if we re-divide by3 for the shuffler selection we get 1/9 still not the same as the presented formula).
We can check the rest of options (less than 50% of N) to be sure the enumeration of all cases add up to 81 so we are not wrong.
.
-2,2,0 ==⟩3*6=18
-Divide them into 2 groups in 3 ways?
AB,CD/AC,BD/AD,BC
that’s it
-now arrange the 3 partitions (these two& zero)in the 3 groups in 3!=6 ways

2,1,1==⟩ 66 =36
1st two& their group in 123/2=6ways
The arrangement in the groups in 3!=6 ways
AB,C,D/AB,D,C/C,AB,D/C,D,AB/D,AB,C/D,C,AB
AC,B,D/AC,D,B
AD,B,C/AD,C,B
BC,A,D/BC,D,A
BD,A,C/BD,C,A
CD,A,B/CD,B,A
.
Total=3+24+18+36
=81 ✓

If u find this example hard to follow check the case when X=3 (P=3/15=0.2)
.
A,B,C
A(1,2,3),B(1,2,3),C(1,2,3) 27 ways
3,0,0 ⟩ 3 ways
Prob(≥50%)=3/27=1/9
check the rest:
2,1,0 ⟩ 332=18ways
1,1,1⟩ordering=3!=6ways

total=3+6+18=27 ✓

If u get it now, check the case where P=1/3, ie X=5 like N, we have the possibilities:
5,0,0 ==⟩ could happen in 3 ways
4,1,0 ==⟩ 30
5 ways to choose the single one* 3!=6 to arrange
3,2,0 ==⟩60
54/2=10 to choose 3 out of 5, then * 3!=6 to arrange
3,1,1 ==⟩60
54/2=10 to choose 3 out of 5, then * 3!=6 to arrange
2,2,1 ==⟩90
5 to choose the single one, * selecting 2of4 43/2=6, /2 divided by 2 for the order of the 2 elements partitions doesn’t count, 3!=6; ie 566/2=90

Total no of ways =3⁵=243
Prob(≥50%)= (3+30+60+60)/243 =153/243 =51/81 … ≥ 0.5

If we divide by 3 again for the o/p of the shuffling is only 1 committee
51/243=0.209

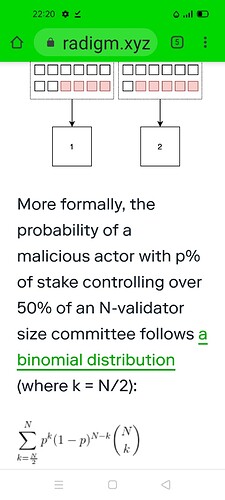
Now let’s get back to the formula in the article & substitute with N=5 for both values of P to see the difference in the results:

When X=3, p=0.2
the summation has only one term
Prob=(0.2)³ (0.8)²10
=864/10⁴= 0.0512
»»»» Does NOT equal 1/9
If we tried to divide by 1/3 (maybe this is his point)
1/27~0.037037…
still NOT the same
.
When X=4, P=4/15, 1-P=11/15
The summation has 2 terms 4,1 and 3,2
Prob= (4/15)⁴(11/15)5 + (4/15)³(11/15)²*(54/2)
=(4³/15⁵)115[4+112]
=(641126)/(3*15⁴)
=18,304/151,875
=0.12052
»»»» Does NOT equal 1/3
If we tried to divide by 1/3 (maybe this is his point)
1/9~0.11111…
still NOT the same

When X=5, P=1/3, 1-P=2/3
The summation has 3 terms 5,0 & 4,1 & 3,2
Prob= (1/3)⁵ + (1/3)⁴(2/3)5 + (1/3)³(2/3)²*(54/2)
=(1/3)⁵ [1+ 25 + 410]
=51/243
Only in this case when X=N, the probability is the same as after selecting a group at random, but this is a special case; and yet the probability is not very small though

.
I know I didn’t derive a fixed formula or recall an existing one from the literature yet, but at least this to point out the written one is not accurate?

2

What’s wrong?
Why there’s absolutely no comments?
Could it be that no body cares which of the two Probability calculation is correct???

3

The use of the binomial coefficient assumes that validators are being sampled from an infinite pool, and are being put into one of two groups: (i) honest, (ii) attacker. The use of the formula is trying to figure out the probability that at least 50% of the sample are attackers.

In reality, the pool is not infinite, but it’s extremely large (~200,000), so it’s a mathematically totally okay approximation.

4

I understand we have pool of size NM very large (actually NM=196,000), with probability P that a person of NM is malicious, So here yes we can assume about X where P=X/NM are expected to malicious.
However, this is not the end of ur case:
you “randomly” divide those NM into M groups of size N each, then u again “randomly” take one of these groups
Now, what we need to calculate is the probability that {at least N/2 of those N items are not malicious}*
(as a function of P or X, then find a threshold that make the probability ≥ 0.5 or maybe larger ratio)
.
If u checked the recalculation of ur simple example of only 2 groups (M=2, N=12, X=9) you will see there is a difference in the probabilities

-Total # of ways malicious can fall in groups is 2⁹=512
( each is indep, and have 2 options)
-The case 4,5 u r describing (no malicious majority threat) can be reached by:
1-choosing 4 out of 9
9876/4! = 9876/24 = 376=126
2-The 4&5 can be arranged in 2 ways (which in group1 & which in group2)
»»»total # of ways for(4,5) = 126*2=252
This is less than half (512/2=256), exactly 0.49
.
-u can re-check the answer by calculating the remaining probabilities for
(9,0),(8,1),(7,2),(6,3) where a malicious majority does exist in one of the 2 groups
They’re in the same order
2+18+72+168=260 ≥ 0.5
»»»
Only u may say it’s still safe because one of the 2 groups is chosen at random, ie divide by more 2 ~0.26 but it’s still a considerable probability

(I wrote it here
Probability of a malicious validator controlling majority of a 6125-size committee · GitHub)
…
.
*{}
I corrected what is between the curly brackets after I was notified by “vbuterin” that I wrote it wrongly in this comment

5

Now, what we need to calculate is the probability that all of those N items are not malicious

Actually, we want the probability that >= 1/2 of the items in the N are malicious.

If u checked the recalculation of ur simple example of only 2 groups (M=2, N=12, X=9) you will see there is a difference in the probabilities

Of course the results here will be very different from the simplified formula, because here M=2. In the real world, M = 2048, so taking M = \infty as an approximation is much more reasonable.

6

Yes I mis-wrote it but only in the previous comment, All the calculation I made are for the probability of:
at least one of the M groups having at least (N/2) of the X (P=X/NM) malicious
.
I start by assuming that every malicious fall uniformly in groups (probability 1/M of being in any of the M groups)
.

M=32 or 2048???
In the actual case, the numbers are not even that large to assume infinity
N=6125, M=32, even 196,000 ≤ 2¹⁸ in the hash crypto world cannot be considered infinity.

Roughly, if there’s 10% malicious it means 19,600 which can fill 3 groups (calculate the probability of this happening & multiply by 3/32 the probability of one of those committees being selected), or(means +) be more than half of 6 groups (probability of happening*6/32),…etc
.
Maybe my analysis is not sufficient, but I suggest u ask someone specialized in probability & statistics

7

Why didn’t u try it as a random Simulation in code, instead of just coding the probability u calculated?
.
Rethinking about it, I believe what u calculated as Bernoulli trials is (infact as u said too, but I didn’t notice at first read) the probability of withdrawing N from an infinite pool, is this the situation here?
I mean do u believe just selecting N at random will lead to the same probability as random partitioning to M committees then random select of one???
Do u think the shuffling process and also M, the no of committees, absolutely has no significance here???

8

Ah sorry you’re right, M does equal 32 and not 2048 in this specific case. But even still, I think it’s close enough to the M = \infty case.

I mean do u believe just selecting N at random will lead to the same probability as random partitioning to M committees then random select of one???

Yes, here’s the reasoning.

  1. Sampling with replacement \approx sampling without replacement (we agreed on this above)
  2. Partitioning to M committees and selecting one = sampling size_of_committee without replacement [these are mathematically equivalent operations]
  3. Therefore, sampling with replacement \approx partitioning to M committees and selecting one

BTW I have done simulations of similar things before, and they do come out similar.

9

I did not agree on that as a start.

Only, I’m thinking maybe what u calculated could suffice as an “easier to calculate” upper bound to the accurate probability, ie

Could be it is not the correct probability, but the correct probability is sure less than that, so if the upper bound is ≤1/2 maybe we are even much safer.

Still, these are thoughts, I’ve emailed 2 persons specialized in probability & statistics and waiting for their reply.

10

M is irrelevant unless we care about joint probabilities, meaning what happens to all 32 committees at once. If we only care about probabilities for a single slot, we can completely ignore the other ones.

The correct distribution to use is the hypergeometric distribution, which deals with the same events as the binomial distribution, but without replacement. With 200000 validators to sample from, there is hardly any difference though. If you run this code (whose outputs are below), the first output gives you the actual probability of having an honest majority in a committee, for a few possible percentages of honest nodes, and the second output gives you the error when computing the same probabilities with a binomial distribution rather than hypergeomtric. As you can see, the error is negligible.

from scipy.stats import hypergeom

from scipy.stats import binom

N = 200000

M = 32

n = int(N/M)

print(f"(percentage of honest nodes, probability of honest majority in committee): {[(p,1 - hypergeom.cdf(n*0.5, N, int(p*N), n)) for p in [0.505, 0.51, 0.52, 0.55]]}")

print(f"(percentage of honest nodes, error of binomial): {[(p, abs(binom.cdf(n*0.5, n, p) - hypergeom.cdf(n*0.5, N, int(p*N), n))) for p in [0.505, 0.51, 0.52, 0.55]]}")

(percentage of honest nodes, probability of honest majority in committee): [(0.505, 0.7853583581880405), (0.51, 0.9445110324526311), (0.52, 0.9993163648690795), (0.55, 0.9999999999999996)]
(percentage of honest nodes, error of binomial): [(0.505, 0.003651190276403704), (0.51, 0.0028686951770731106), (0.52, 0.00012987274559679357), (0.55, 8.066149621078799e-16)]
11

I think we care about all the M committees, as we will choose one of them at random after they have been all formed
.
It seems u look to the problem as withdrawal of N from the whole population with/without replacement, I look to it as it will happen exactly ( as described by Vitalik Buterin) : u shuffle the whole population into M committees each of size N then select one of them at random, this is supposed to give more randomness and thus leads to an average malicious ratio more nearer to the original P.
If u have written a simulation code, why didn’t u write it to the exact problem?
I mean with the shuffling & selection step???
-I will try again to ask specialized professors in probability & statistics. Vitalik is also suggesting another method that I haven’t completed reading it yet, maybe we can check which leads to better probability ( less probability of malicious ≥ N/2)

.
Ps.
Strange ur 23hr ago reply, just appeared now in my browser