Overview
This post discusses constructing dissociation set (proof of non-membership) discussed in the Privacy pools paper, evaluating potential drawbacks. We also discuss using KZG commitment scheme to achieve the same goal, again evaluating advantages and drawbacks.
Background on Privacy Pools
UTXO-based shielded pool in many privacy protocols uses an incremental merkle tree to store UTXO commitment of an asset. Most commonly, the assets are represented as leaves in the merkle tree in the form of commitment = hash(amount, blinding, pubKey). When spending an asset, users will generate a zero knowledge proof that it has the corresponding private key to spend it. When an asset is spent, a nullifier in the form of nullifier = hash(commitment, merklePath, sign(privKey, commitment, merklePath)) is published so that no commitment can be double spent.
Privacy pools proposed that users or independent third party providers can select a subset of the commitment notes to form a separate merkle tree. Users can then prove that the commitment note that they withdraw from the shielded pool is part of the selected notes using a zero knowledge proof of membership (named as association set in the paper). This is done when the selected notes are a set of whitelisted deposit notes. Alternatively, when a set of blacklisted notes (e.g. notes that are involved in smart contract hacks) are selected to form a merkle tree, users can generate a zero knowledge proof of non-membership to prove that the commitment note is not part of the set (known as dissociation set in the paper).
Constructing dissociation set
Constructing an association set is fairly straightforward using proof of membership on a merkle tree. There are many open source implementations such as Semaphore.
Constructing a dissociation set comes with more challenges in terms of cost. Two common ways to construct a dissociation set using merkle tree are as follows:
Sparse merkle tree
A sparse merkle tree is a tree of the same size of the incremental merkle tree that contains the deposit note. Deposit notes have the same index in both trees (e.g. if the deposit note is a leaf at index 0 in the incremental merkle tree, it will also take position of index 0 in the sparse merkle tree). Each leaf in the sparse merkle tree can be a bit value, where 0 indicates that the deposit note is not blacklisted, and 1 indicates that the deposit note is blacklisted (or any arbitrary value really). For a user to prove that its deposit note is not blacklisted, it can generate a zero knowledge proof that shows the for the corresponding index, its deposit note evaluate to 0.
A drawback of using a sparse merkle tree is storage inefficiency since we need the size of the tree to be the same as the deposit note tree. Most leaves in the sparse merkle tree simply stores value of 0. A larger merkle tree implies that the depth of the tree is larger, and any updates to the leaves means that we need to perform more hashes on-chain in order to arrive to the new root.
Ordered merkle tree
An ordered merkle tree is a tree where deposit notes in the tree are ordered. We could collect all blacklisted deposit note, order them, and put them into a merkle tree. To prove that a deposit note is not part of the merkle tree, the user has to generate a zero knowledge proof that shows a few conditions:
- The deposit note has a value larger than leaf at index i but smaller value than leaf at index i+1
- The two leaves at index i and i+1 must be separated by one index in the merkle tree
A limitation of such construct is that when a new blacklisted deposit is to be added to the dissociation set, we will need to reconstruct the merkle tree. There is no efficient way to insert a new leaf since the order of the merkle tree needs to be maintained.
Alternatively, we could use an indexed merkle tree, where each leaf has a pointer pointing to the next leaf in order (Aztec wrote a really good piece on it). With an indexed merkle tree, we don’t need to reconstruct the tree when a new deposit note is added, instead we will slot the deposit note in order and update the pointers. This makes inserting a new leaf easy and cheap, however to find the adjacent leaves in the tree might involve brute forcing through the entire list of leaves (since they are not technically ordered and only relies on pointer to keep the ordering).
Using KZG to construct dissociation set
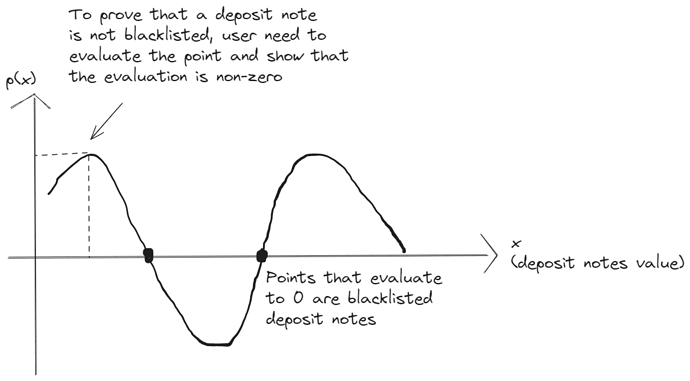
KZG is a polynomial commitment scheme widely used in cryptography and zero knowledge proof construction. We can use KZG to construct the dissociation set. Essentially a set of blacklisted deposit [D_0, D_1, D_2, ...., D_n] will be points on the polynomial, and we can arrive to the polynomial equation using lagrange interpolation. We can set this points to evaluate to zero on the polynomial (so they are all roots of the polynomial).
The polynomial is then committed using KZG. When a user would like to prove that its deposit is not blacklisted (let’s denote the deposit as D_i), the user just needs to evaluate the polynomial at point D_i, and show that the evaluation does not equal to zero.
A few advantages of using KZG to construct the dissociation set as compared to using merkle trees:
- KZG proof size is constant and small - for example, for the elliptic curve BLS12_381, the proof size is only 48 bytes.
- We can easily edit the committed polynomial so flexibility to add or remove blacklisted deposits using linear combinations
- For example, to add a deposit d into blacklist, we need to modify the evaluation of d at the polynomial such that it equals to zero. Supposing the initial evaluation at point d is initially a, and we want to change it to b (zero in this case), the commitment of the new polynomial will simply be
commit(new_poly) = commit(old_poly) + (b-a) * commit(lagrange_poly_d)
- For example, to add a deposit d into blacklist, we need to modify the evaluation of d at the polynomial such that it equals to zero. Supposing the initial evaluation at point d is initially a, and we want to change it to b (zero in this case), the commitment of the new polynomial will simply be
- KZG also supports multiproof so a user can prove multiple deposits are not in the dissociation set, while still keeping the constant proof size
The last remaining open question is that how could a user protects its privacy when generating the proof of non-membership? Evaluating the polynomial at point D_i also means revealing the deposit note owned by the user. To maintain the privacy of the deposit note, users can generate a zero knowledge proof of the KZG evaluation instead.
Depending on the elliptic curve that we use for the KZG commitment scheme, one of the drawbacks is introducing development complexity and cost. For example, the BLS12_381 curve commonly used is KZG is not a supported precompile in Ethereum.
Closing thoughts
This post explores using KZG to construct dissociation set mentioned in privacy pools. In fact, a similar concept was also mentioned in a post by @vbuterin, where KZG is used to prove keystore ownership. I would greatly appreciate feedback on tradeoffs and would welcome a discussion on its feasibility. A further work is to run cost and gas benchmarks on the merkle tree and KZG approaches respectively.
Credits to Aciclo and the Chainway team for discussions.