In building the Placeholder proof system for =nil; Foundation, we use a lookup argument based on the Plookup paper by Aztec researchers. We took Plookup technique as a starting point and then made some practical improvements for writing large PLONK circuits with a complex logic.
Lookup argument allows prover to prove that some table over prime field (hereafter assignment table) satisfies specific constraints: some cells computed from assignment table (lookup input) belong to list of values that is also computed from the assignment table (lookup table).
Join-and-split algorithm
The core of Plookup techinque is a sorting algorithm. We call it join-and-split because it includes two steps:
- join — lookup table columns are joined together with input columns into single large vector using special reordering algorithm.
- split — constructed vector is split again into original size parts.
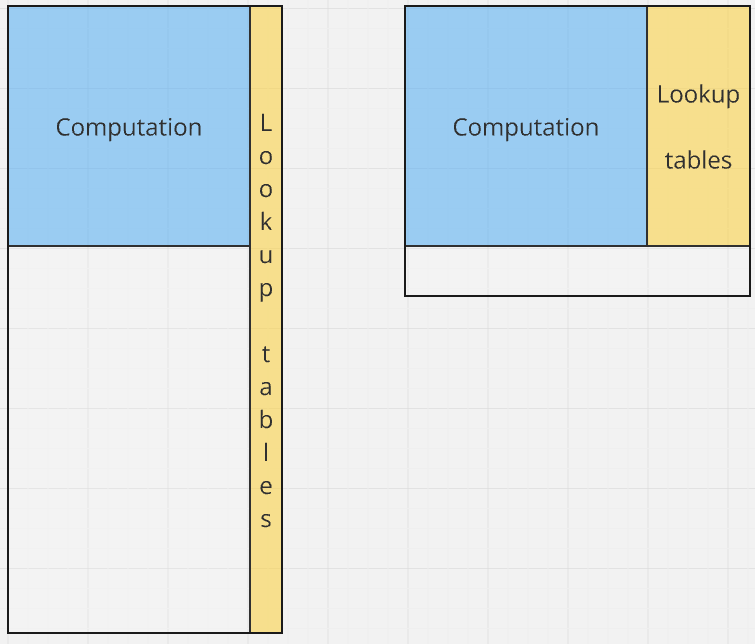
The case with the single lookup table and single input column is described in the Plookup paper in detail. But it wasn’t enough for our use-cases. We needed lots of efficiently packed lookup tables and lookup constraints applied to arbitrary rows and columns, and we didn’t want to repeat lookup argument for each (input, table) pair.
So, we modified join-and-split algorithm to be able to join more than two columns. It allows us to use multiple lookup constraints even if they are applied on same rows and use a large lookup table, even if its size is greater than the whole assignment table rows amount by appending columns to assignment table instead of rows. Balance between assignment table rows and columns amounts helps to find a perfect balance for the best prover performance and verification cost.
Selector columns
Original article contains technique to lookup tuples of values that are placed in the same or neighboring rows. It constructs linear combinations of columns with a random factor. Combining this approach with polynomial expressions usage for lookup tables and input columns both we achieved selector columns full support. Circuit designer now can manage which rows exactly are constrained and what rows are reserved for lookup tables storing.
Plookup paper also describes technique for multiple lookup tables support. They propose to associate each lookup table with its unique identifier and fill tag column to mark what rows contains lookup tables with which identifier. Tag column for input helps to mark what constraints are applied to marked row. Tag columns should be a part of the random linear combination constructed for the lookup table and input columns respectively. This approach is obviously limited. Sum of lookup tables sizes should be less than the whole table rows amount.
We combined lookup table identifier usage with our selector columns construction and algorithms for large lookup tables. These modifications allow lookup tables to be stored and used without regard to lookup argument restrictions, but according to the best circuit design. It made our lookup argument into a universal and flexible tool.
Detailed description of our modifications can be found on our HackMD page. Feel free to share your comments!