Make EIP 1559 more like an AMM curve

Economics
,
1

See also: ideas near the end of this thread that led to this concrete proposal.

Consider a version of EIP 1559 that works as follows. The protocol maintains a parameter, excess_gas_issued. The protocol has a pricing function:

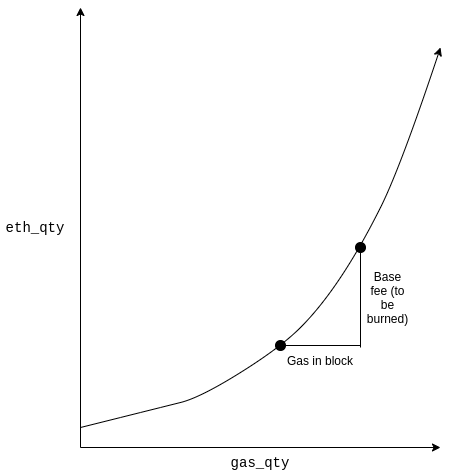
eth_qty(gas_qty) = exp(gas_qty / TARGET / ADJUSTMENT_QUOTIENT)

Where exp(x) \approx 2.71828^x. In an actual implementation, this would of course be replaced with an integer-math-friendly approximation, but it’s mathematically cleaner to think of the above formula.

When a block proposer wants to make a block that contains gas_in_block gas, they need to pay a “burn fee” equal to eth_qty(excess_gas_issued + gas_in_block) - eth_qty(excess_gas_issued):

ethqty

After the block is processed, we set excess_gas_issued = max(0, excess_gas_issued + gas_in_block - TARGET).

The analogy here is that the blockchain manages a pool of gas, which block producers have to “buy” according to a constant-function automated-market-maker curve. Block producers can buy a maximum of SLACK_COEFFICIENT * TARGET gas in a block (eg. SLACK_COEFFICIENT = 2). Additionally, in every block, a virtual agent “sells” an extra TARGET gas.

This creates a mechanism very similar to EIP 1559. The “basefee” equivalent here is the derivative of the curve at the current excess_gas_issued value, so basefee = eth_qty(excess_gas_issued) / (TARGET * ADJUSTMENT_QUOTIENT) (remember basic calculus for how \frac{d}{dx} e^{kx} is computed).

But this mechanism is superior in two key respects:

  1. We have a hard invariant for how to compute the basefee as a function of excess_gas_issued. This ensures that over time, excess_gas_issued is bounded, meaning that long-run gas usage is guaranteed to be very close to TARGET * (number of blocks). There is no fancy trick that you can pull with moving transactions between blocks to make long-run average usage per block be anything other than TARGET.
  2. It is resistant to the instability scenario where there are many transactions whose max-basefee is N and the chain jumps between 2x-full blocks with a basefee of N * 0.9 and empty blocks with a basefee of N * 1.0125. This is because even the formula within a block is nonlinear, so if the gasprice starts off at N * 0.9 with an ADJUSTMENT_QUOTIENT of 8, you would expect to see one block with TARGET * 0.843 gas followed by a chain of blocks with TARGET gas.

Note that because of the nonlinearity of the burn, EIP 1559 would need to be adjusted. There are a few options:

  1. The proposer pays the burn and the full fees from the transactions (including the basefee component) go to the proposer. Note that this still requires an algorithm to determine how high the basefee is considered to be in transactions that specify their gasprice in the form basefee + tip.
  2. The transaction origin pays a basefee equal to the maximum it could pay (that is, the basefee at excess_gas_issued + TARGET * SLACK_COEFFICIENT), and then at the end of block execution, everyone gets refunded so that the end result is that everyone pays the implied average basefee (the “implied average basefee” is (eth_qty(excess_gas_issued + gas_in_block) - eth_qty(excess_gas_issued)) / gas_in_block; the refund is the difference between the originally paid basefee and this amount)
12 Likes
2

Very clean design!

With the average implied basefee payment (or likely any basefee determination rule that depends on the number of transactions included in the block) there is a non-trivial optimisation problem for the miner to solve due to the interaction between the transaction tip = min(premium, fee cap - basefee) and the transaction fee cap. For instance, a high premium but low fee cap transaction may become less valuable to include in a larger block (with higher implied basefee), vs a low premium but high fee cap transaction. This was already noted to figure out how the transaction pool should be reordered and accessed under EIP-1559. There are likely good heuristics around this issue, in fact likely the same ones that transaction pools will use.

With initial simulations based on the abm1559 library it does seem to be the case that oscillations are not as pronounced with the AMM design vs the classic 1559 update rule (see this notebook for early results).

2 Likes
3

This would definitely penalize a block proposer who uses a lot of gas by charging him a higher price per gas, in contrast to EIP-1559. But it is still the case that the subsequent block proposer faces an even higher price, as he does in EIP-1559.

A spillover of higher gas price into subsequent blocks may be something that we actually want. There are two reasons I can think of. First, it could be because there is an additional cost from having multiple large blocks occur in a short time interval, holding constant the long run average block size. I do not have a good idea about how large this cost is.

Another reason we might want a spillover is that we want to very strictly adhere to the target block size, rather than consider a cost of overshooting the target and optimizing between this cost and providing additional block space. I personally think optimization could be better if we set the right parameters. But even if we were to choose to adhere to the target, keeping the hard cap of 12.5M gas may be better than allowing a flexible block size and misaligning incentives.

Suppose we find that we indeed want a spillover. Even in that case, I think the mechanism should be such that the proposer of the original block faces the highest price, and the price gradually decreases if subsequent blocks hit the target size. This makes sense especially if the rationale for spillover is that we care about large adjacent blocks. If you are farther away from the congestion, your transactions add less to the congestion, so you should pay a lower tax.

1 Like