Median prices as alternative to TWAP: an optimised proof of concept, analysis, and simulation

[hoytech]

Recently there have been concerns raised about the long-term security of Time-Weighted Average Price (TWAP) oracles as implemented by Uniswap, especially related to the Proof of Stake transition and more sophisticated MEV capabilities.

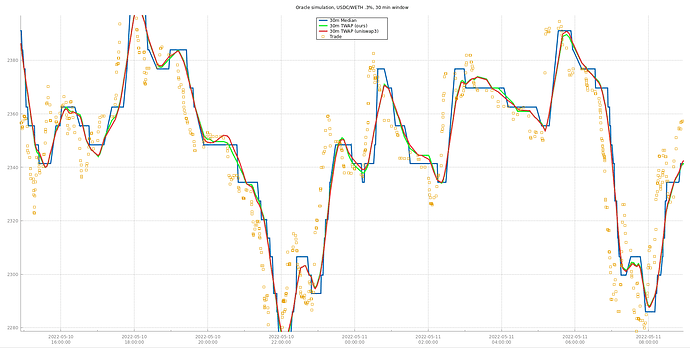
I’ve been working on a new price oracle implementation that computes the median price during a specified window of time. Median is believed to be more secure against attackers who can manipulate an AMM price over several blocks in a row, since the outlier values will be thrown out unless the attacker can persist them for half the window size.

Since this is a ground-up redesign of the oracle mechanism, I’ve also tried to improve on it in some other areas as well:

• Computes both the median and the geometric TWAP concurrently and returns both, so that the oracle consumer can decide which to use.
• If the window cannot be satisfied because the record needed has already been overwritten in the ring buffer, it returns the longest available window instead of throwing an error. Instead, the consumer can decide what to do.
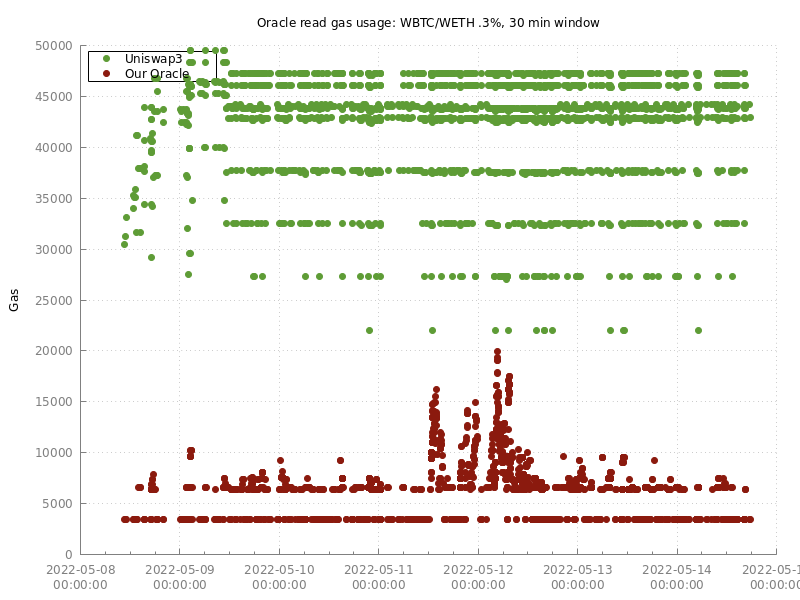
• Typical gas required to read the oracle is much smaller than Uniswap3, and is competitive with centralised oracles like Chainlink for most assets.
• Gas used is independent of the ring-buffer size

Of course there’s no such thing as a free lunch and there are some trade-offs as well:

• Worst-case gas usage is higher than Uniswap3 (although in my opinion this is manageable – see the documentation)
  • In theory, adversarial input data could cause the gas to balloon, although I have a proposed fix for this (comments appreciated!)
• Price resolution is 0.3% (compare Uniswap3 at 0.01%, and Chainlink at 1%)
• The maximum time window that can be requested is 65535 seconds (about 18 hours 12 minutes)
• The time window must always be aligned to the present – you cannot query historical windows
• Only price can be queried, not pool liquidity

I’ve also created a simulation that replays Swap logs from mainnet into my proof of concept as well as a stripped down version of Uniswap3. This lets us compare the resulting prices and gas usage. As a teaser, here’s one of the images output from the simulation:

Check out the docs for a more detailed explanation of how it works. And more pictures: https://github.com/euler-xyz/median-oracle

Thanks in advance for any feedback!

[Evan-Kim2028]

Where is your further justification that “Median is believed to be more secure against attackers who can manipulate an AMM price over several blocks in a row”?

Median price oracle is only more resistant to single block manipulation, but in the case of multi block manipulation the cost is 50% cheaper compared than the arithmetic mean and is EASIER to manipulate. Additionally the geometric mean is much stronger than the arithmetic mean and was the proposed second solution to prevent TWAP manipulations.

See Section V - A. Solution 1: Median https://eprint.iacr.org/2022/445.pdf

The document you linked in your github by Michael Bentley, Nov 2021 (I can’t post the link because I am a “new user”) validates the fact that geometric mean is difficult to manipulate and is only possible when there are very low amounts of liquidity or volume. Relaxing these assumptions seems to be the only way to manipulate TWAP oracles in general, which both papers state.

Assuming the conditions of liquid reference markets and no arbitrage economic conditions hold (normal market conditions) suggests robust oracle-mainpulation tampering of TWAP oracles using arithmetic means https://arxiv.org/abs/1911.03380

[vbuterin]

What kind of multi-block attack do you have in mind? Winning the MEV auction for the first transaction half the blocks in a span, and doing a flash loan manipulation attack in each one of those blocks?

I think there are ways to deal with that kind of attack; a simple one is to take the median of the entire set containing (i) the min price during each block in the span, and (ii) the max price during each block in the span.

The only way to continue an attack in such a situation is to actually push the price up, which opens you up to attacks of potentially unlimited size from arbitrageurs who see what’s going on and want to make a profit.

I do think that the mean being vulnerable to single-block attacks is a really big problem, and eventually it’s going to get exploited, and requiring attacks to run for many blocks in an epoch to have any effect is an important mitigation.

If we don’t want to use the median, another option is to look at the various alternative functions in the Wikipedia article on robust statistics.

[euler-mab]

We had a similar idea regarding the intra-block attack prevention. Rather than use the last swap price on the block as the price that feeds into the TWAP, why not use the mean block price instead? That would be extremely simple and cheap to compute, and make it much harder to position a single large transaction as the contributing price to the oracle. The median would be even better, but perhaps cost a fair bit more gas to compute for heavily traded assets.

Overall, the geometric mean being vulnerable to single-block attacks can also be solved relatively easily, if we accept some constraints on what swappers can do. If there is at least some full-range liquidity, a single block attacks requires a price manipulation of many orders of magnitude above/below the current price (see this analysis referenced by @Evan-Kim2028 above). A simple (and admittedly quite ugly) method of preventing this kind of attack would therefore be to just limit the maximum inter-block slippage on the underlying DEX to something less than (0, \infty).

For example, assume the current price of an asset is $1. A single block attacker looking to raise the geometric mean TWAP price needs to manipulate the spot price on at least one block to billions of $. So to prevent this, we simply limit swaps within a block to [$0.5, $2]. This completely nullifies the single block attack whilst having a minimal impact on (most) swappers. If the real spot price on the wider market is beyond this range then arbitrageurs will surely move in on the next block anyway.

Numeric constraints like this are actually in existence on Uni v3 today, albeit in a much less restrictive form. We discovered that the most you can usually move a 30-minute TWAP by in a single block attack is around 70%, because the manipulated spot price on a single block hits the max tick price in Uniswap.

[hoytech]

I think we may have different ideas about what I mean by median in this context. The way that my proof of concept works is by time-weighting the inter-block prices inside of a time “window” (there’s a pretty OKish image depicting this in the documentation). For example, suppose we choose a 30 minute window. This would on average span 144 blocks (assuming 12.5 second block-time).

For the sake of argument, let’s say there was no trading activity at all for 30+ minutes. In this case, no matter what you moved the price to on the next block it would not affect the median. Same for the following block, and for the next 70-some blocks. By contrast, a TWAP (either arithmetic or geometric) will immediately start moving in the direction of the manipulation. If the “spot” price can be moved a bajillion percent (likely implying, as you note, insufficient liquidity), then the very next block the TWAP may already be at a sufficient level to execute an attack. Michael’s point that the price movement is bounded in how much it can move in a single block due to MAX/MIN_TICK limits is an interesting artifact of Uniswap3’s implementation that we only noticed when simulating these attacks (!). FYI our simulation tool is available here: https://oracle.euler.finance/

After the 72nd block at a manipulated price, the median will immediately “snap” to this bad price, whereas a TWAP would still be catching up. If an attacker’s plan is to hit a target price without manipulating over that target price for some reason, then yes, an argument can be made that median is less secure than TWAP. I also expand on this more in the documentation. In short, it’s not clear (to me at least) if either geometric TWAP or median is universally “best”. That’s why my PoC computes both of them, and individual applications can choose what is best for them.

Regarding arithmetic versus geometric TWAP, I think we should just forget that arithmetic mean was ever applied to this problem. Not only does it provide a sub-optimal level of security, but it also requires twice the storage writes to maintain accumulators if you want to support both the pair and its inverse (just for completeness I’ll note that with my PoC, which doesn’t use accumulators, we could compute arithmetic TWAP without this additional overhead if we wanted to, which we don’t).

Whether geometric mean is difficult to manipulate depends on several things. As you mention, if the liquidity is low (for some value of low) then it becomes easier to manipulate. If the liquidity is less low then maybe it would cost a zillion dollars in losses due to arbitrage just to move the price up (say) 100%. However, if you can steal 1.1 zillion dollars from a lending platform at this new price, then you still come out ahead. If you can censor arbitrage transactions for some number of blocks then this could reduce the costs further (see the conclusion in the first PDF you linked, re: “MMEV”).

BTW when I said “in a row” in my post I was being a bit sloppy, since the manipulations don’t necessarily need to be consecutive – anywhere inside the window will do (this applies to both TWAP and median).

[hoytech]

No, I’m not worried about flash loan-sourced manipulations. Neither TWAP nor “TWMP” can be influenced by pure flash loan manipulations, since those must be repaid within 0 seconds (and if the flash loan is repaid by moving the price back, then this price’s time weight is 0).

I’m mostly worried about situations where an attack can censor transactions from other users. Here’s a possible(?) example, post PoS: An attacker learns that he will have the privilege of making block N. On block N-1, he uses flashbots and some free funds to move the price some gigantic amount (possibly also using up the rest of the gas in the block to prevent any later TXs from arbing it). Then on block N, he moves the price back, recovering the funds minus fees, and uses the now-changed price to execute an attack on a lending protocol (without needing to pay any MEV because of course he’s censoring other people from arbing it and/or front-running his lending protocol exploit).

This is sort of a like a “single-block” attack, although I’m not sure there’s actually a categorical distinction betwen single/multi block attacks here. What if the attacker by chance gets two blocks in a row (or is colluding with another validator). In this case, the attacker can censor transactions for two blocks, meaning the manipulated price could be moved further and/or a smaller amount of free funds would be needed. Similar for 3 blocks in row, etc. At some number you have to figure the chances of the attacker controlling all the blocks by chance is impractically low (what is that number I wonder?). Oh, and multiple “N-block” attacks within a window would also suffice as they don’t necessarily need to all be consecutive.

Note: I did not come up with this attack, it’s being discussed in a shared doc between flashbots/uniswap/euler. There are a bunch of other variants.

Your idea about taking the median of min and max prices achieved in each block within the window is interesting. Would it have an advantage over the simple time-weighted median? My first thought is that computing the median itself would require more work since you would have two data points per record instead of one. Also, unlike TWAP/TWMP it does still incorporate prices that could be achieved with flash loans, which I kind of prefer to disregard as “fake news” prices.

[Evan-Kim2028]

oh! I see what you mean now. This is an interesting idea I see what you are trying to do now.

Regarding the simulation chart that shows the 30m median vs TWAPs, the median price is much more “coarse” than the mean, reasonably so. Would you consider this a more efficient price path for users?

Alternatively an efficient markets argument could be made here that having a consistent arbitrage between Median and TWAP liquidity pools will create more robust markets and efficient markets overall so my earlier question would be moot.

[hoytech]

I’m not necessarily suggesting that the price returned by the oracle actually be used by the AMM for price quotation purposes and in fact was not at all considering that during design. For example, Uniswap does not do that: Its oracle output is solely a view into historical trading activity and has no direct impact on present or future prices offered.

That said, theoretically the oracle output could be used as “feedback” into the AMM. I believe Curve v2 works like this using an exponential moving average to control where to concentrate liquidity. EMAs are similar to TWAPs except they are IIR instead of FIR filters, which was probably necessary due to gas constraints.

[ptrwtts]

Would it be accurate to describe this as “Time Weighted Median Price”?

[hoytech]

Yes, I would say so. What it measures is very similar to TWAP, but replaces the averaging with a median selection. However, the underlying algorithm used to compute it efficiently is drastically different than those used by previous TWAP implementations.

[TylerEther]

Why not use the weighted harmonic mean?

Harmonic means are a much more accurate way of describing averages when dealing with rates.

[hoytech]

Can you please expand on this a bit? Are you asking why use a median instead of a harmonic mean?

With a median, outlier samples are not incorporated into the output at all. My hypothesis is that this will make oracles harder to manipulate. Harmonic mean is still a mean, and a single “very bad” input value can have a drastic impact on the output.

For example, take the sequence [1, 1, 1e-9]. The harmonic mean of these values is:

3/(1/1 + 1/1 + 1/1e-9) = 3e-09

… whereas the median is 1.

[TylerEther]

Thanks for stating your hypothesis. I now see that my mention of using a harmonic mean is a bit off-topic. I can expand on my thoughts regarding harmonic TWAPs if anyone is interested.

I see medians as being harder to manipulate as outliers will be ignored, and it’ll be required to manipulate the price for 50%+1 of the period. This assumes there’s no manipulation of the recorded observations, which is another story.

While medians may be harder to manipulate, there’s a trade-off in responsiveness. What happens when the price legitimately increases or decreases quickly? When used in lending protocols, we want to be able to liquidate unhealthy accounts before they go underwater. Using a median, in this case, could cause some problems and require lower collateral factors to be used.

Nevertheless, this is exciting work!

[hoytech]

Thanks!

Yes, there are certainly some trade-offs between using median and averages (of various sorts). You’re right that an average will begin to respond faster than a median to a “legitimate” price change. However, another way to look at it is that half-way through the window duration, a median will immediately jump to the new price level, whereas the average will still be reporting “stale” rates for the next half window duration. In this sense, a TWAP is less responsive than a median of equivalent window size.

To me it’s not totally clear which is better in all circumstances, which is why my PoC in fact calculates both the geometric average and the median at the same time and lets the caller decide which to use.

One aspect of Uniswap3’s oracle interface that I intend to improve on is to allow users to efficiently query for a range of historical data in a single call, so that alternate averages, volatility measures, etc, can be computed by external contracts. Getting this data with Uniswap3’s interface is expensive and cumbersome.

[apoideas]

Hi @hoytech, thanks for posting this great idea, convo, and research.

Looking at the gas use images from the linked github, I have a practical question that I am trying to understand:

How much does it cost for a dApp to use a UniswapV3 TWAP? In the case of Euler, does an observation need to be called every block, and for every asset that currently has open trades? From your plotted charts, it looks like a TWAP oracle observation costs between 25-50k gas. It seems like having to pay this over hundreds of blocks, if you had to make successive TWAP observations, would quickly become prohibitively expensive, so I feel I must be missing something re: how an application interacts with TWAP oracles.

I would appreciate some insight here, so thank you very much, sir.