Abstraction
I implemented an append-only merkle tree data structure with
- Appending new data with O(1) writes.
- always 2-3
SSTOREs no matter how many data it has (1 non-zero slot, 1-2 zero slots)
- always 2-3
- Querying merkle root with O(log{n})
- Less efficient than original merkle tree but it’s reasonable complexity.
- Even though it has O(logn) complexity, you can reuse it with O(1) if caching.
- You don’t need to save merkle root histories. You can calculate them anytime without saving them.
- Auto-Incremental level (depth) of merkle tree. (pre-defined depth not required)
- It is also possible to modify, but it needs about O(log{n})
SSTOREs same as original merkle tree.
I call it as CMT(Confirmed Merkle Tree) for convenience. I think it is useful for maintaining merkle trees
especially in EVM based smart contracts.
Performances
I opened source code : GitHub - 0xall/confirmed-merkle-tree
I implemented CMT by solidity for testing. I made a merkle tree with dummy data and test
its append and root query performance. It gets average gas costs by appending and querying 128 times. I use keccak256 algorithm but, of course, using other hash would work well.
Please do not use production level yet because it’s not audited.
Append performance (gas fee in EVM)
| dummy size | average gas fee |
|---|---|
| 2^16 - 1 | 79804 |
| 2^32 - 1 | 79804 |
| 2^64 - 1 | 79804 |
As you can see, append costs small gas fee no matter how many data it has. it uses 1-2 zero slot SSTORE and 1 non-zero slot SSTORE.
Query merkle root performance (gas fee in EVM)
| dummy size | average gas fee |
|---|---|
| 2^8 - 1 | 92160 |
| 2^16 - 1 | 146426 |
| 2^32 - 1 | 281750 |
| 2^64 - 1 | 569950 |
You can see it costs incrementally with O(logn), but it’s reasonable. In most cases, the size is less than 2^32. Also, you can reuse merkle root with O(1) if cached once.
My implementation is not optimized. It calls query function by recursive. I think there are additional optimizations by reducing memory and stack size.
Background
Merkle trees are widely used for data validation in smart contracts. It could be achieved with low gas fee because we just put only merkle roots to smart contracts.
In some cases, the reliability of merkle root is also important. Especially, contracts which are using
ZKP(Zero-Knowledge Proof) (ex. zk-SNARKs), they should maintain merkle trees. However, to maintain all merkle tree nodes in smart contract, it requires O(log n) for every appendation and it’s expensive in EVM.
So, I’ve done deep dive into how to maintain merkle trees efficiently in smart contract. Not only in smart
contracts but in other systems (such as centralized servers), it is useful.
Basic Idea
The total number of nodes in merkle tree is 2^{\lceil log_2{N} \rceil + 1} - 1 \approx 2N (including
zero-value nodes that not appended). It implies that we can maintain merkle tree if every append
contributes only 2 nodes. So, we make some constraints to achieve it.
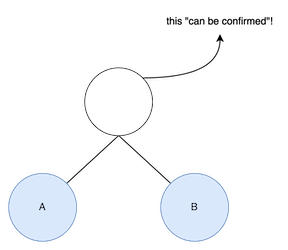
If node has two child nodes, we can calculate its value with hash(L, R). I’ll call it as “comfirmable node”, and if it is inserted into merkle tree, I’ll call it as “confirmed node”.
Every append, we should insert merkle tree nodes with constraints below.
- CMT inserts only “confirmable node”.
- CMT inserts maximum two “confirmable nodes” per an append.
Details
Where we should insert nodes
There is a problem : where to insert nodes.
We should insert one or two confirmable nodes for every append. There is a trivial node that can be confirmed for every append: it’s leaf node. We should insert one leaf node for every append first.
For example, assume that there is a merkle tree such like that.
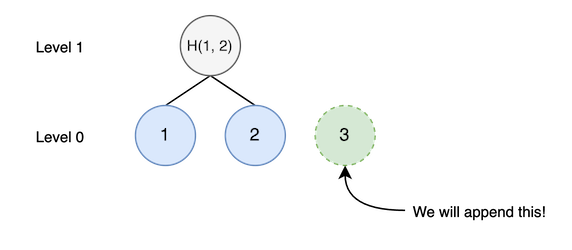
Let’s insert new node. We should insert third node in level 0 (=leaf node level).
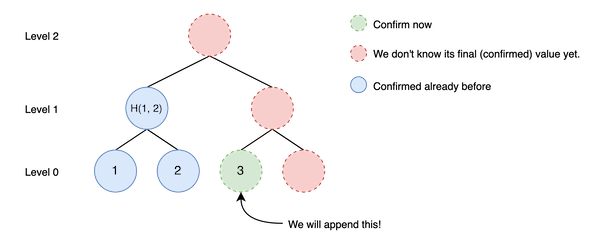
Next, we should confirm other node. (second constraint: insert two nodes per an append) But we
can’t insert anymore since there is no node that can be confirmed (first constraint: only inserting
node can be confirmed). So, in this case, finish appendation.
Let’s see other example.
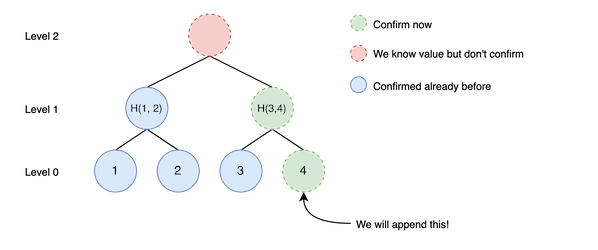
In this case, there are two node that can be confirmed. So, we can insert just two nodes. After inserting, root node can be also confirmed but we don’t confirm it because of second constraint.
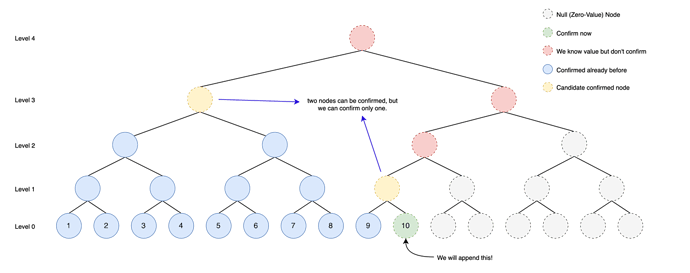
How about this example?
In this case, there are three confirmable nodes. By second constraint, we should insert two of them. Because we have to insert leaf node for every append, we should select one of two nodes (excluding leaf node) to insert.
So, we have to make a rule for getting confirmable node index to insert. I suggest a good formula working well.
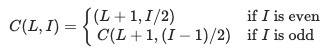
for level L and index I in CMT. (index starting with 1) If we should append nth leaf node, you can calculate confirmable node level and index by C(0, n). So we just have to insert leaf node (0, n) and C(0, n) node for every append.
The result of C(0, n) always returns confirmable node if I \neq 0. If I = 0, we can just ignore it.
(only confirm leaf node).
By this, you can maintain merkle tree with O(1) append and O(log n) querying merkle tree.
Proof
We can know when the node inserted from formula.
If L = x - 1 and I = 2y + 1, then C(x, y) = C(x - 1, 2y + 1) since 2y + 1 is always odd.
We can get C(x, y) = C(0, z) by sequence f(n+1) = 2f(n) + 1.
f(n+1) + 1 = 2 (f(n) + 1)
\frac{f(n+1) + 1}{f(n) + 1} = 2
\prod_{i = 1}^n \frac{f(i) + 1}{f(i - 1) + 1} = 2^{n}
So, f(n) = 2^n (f(0) + 1) - 1 and C(x, y) = C(0, 2^x (y + 1) - 1).
Therefore, (\alpha, \beta) = C(\alpha - 1, 2 \beta) = C(0, 2^{\alpha - 1} (2 \beta + 1) - 1)
So, it means the node (X, Y) is inserted only if (2^{X-1} (2Y + 1) - 1)-th leaf node inserted.
\qquad \cdots \quad \mathbf{A}.
When we insert n-th data to CMT, we also insert C(0, n), so C(0, n) should be confirmable node. Let’s prove that C(0, n) is always confirmable node.
First, assume that there exists (X, Y) node inserted in CMT. By \mathbf{A}, the number of leaf nodes has to be greater than or equal to 2^{X-1} (2Y + 1) - 1.
The (X, Y-1) node must be also inserted already because it was inserted when (2^{X-1} (2Y - 1) - 1)-th node inserted and 2^{X-1} (2Y + 1) - 1 > 2^{X-1} (2Y - 1) - 1.
So, if (X, Y) node confirmed, (X, Y-1)-th node also confirmed. \qquad \cdots \quad \mathbf{B}
Now, let’s prove that C(0, n) can be always inserted when n-th leaf node inserted.
If n is odd, (1, (n - 1) / 2) node is also already confirmed because it should be confirmed when (n - 1)-th leaf node inserted by \mathbf{A}.
If n is even, (1, n/2) is confirmable because (0, n-1) and (0, n) (its two child nodes) are confirmed.
Assume that (X, k) is already confirmed and k is odd. It means the number of leaf nodes should be greater than or equal to 2^{X-1} (2k + 1) - 1.
(X + 1, (k - 1) / 2) node should be also confirmed because it should be confirmed when (2^X k - 1)-th leaf node inserted and 2^{X-1} (2k + 1) - 1 > 2^{X} k - 1.
Assume that (X, k) is already confirmed and k is even. By \mathbf{B}, (X, k-1) is also confirmed already. (If k is 0, there is no such node because index starting with 1. In this case, we just confirm only leaf node.) So, excluding that, (X+1, k/2) node is confirmable.
By mathematical induction, when leaf node (0, N) inserted, C(0, N) is always confirmable. (except I=0)
Querying merkle root
Because we only insert confirmable nodes, there are some unconfirmed nodes in CMT. When C(0, N) = C(E, 0), we can’t insert it since index staring with 1 so index 0 not existing. Since C(E, 0) = C(0, 2^{E-1} - 1), we can insert only leaf node when appending 1st, 3rd, 7th, 15th, …, and (2^n - 1)-th append. So, there are 2N - \lfloor{log_2{(N + 1)}} \rfloor confirmed nodes when the number of leaf nodes is N. Since there exists 2^{\lceil log_2{N} \rceil + 1} - 1 \approx 2N nodes in merkle tree, there are about \lfloor{log_2{(N + 1)}} \rfloor unconfirmed nodes to be calculated for getting merkle root in CMT.
Therefore, it requires O(log n) storage read operations.
Fortunately, in most systems (including ethereum smart contracts), loading from storage is cheaper than writing. So, it’s more efficient. Besides, merkle root can be cached! So, if we store it when we read once, we can get it with O(1).
Also, there are some optimizations for querying merkle tree.
- we can pre-calculate null-value ( \phi ) hash list.
\phi,\ Hash(\phi, \phi),\ Hash(Hash(\phi, \phi),\ Hash(\phi, \phi)),\ ...
Also, we can check whether all leaf nodes from node (L, I) are null-value by I 2^L > N.
- We don’t have to read unconfirmed nodes for checking it’s unconfirmed since we know it by \mathbf{A} in proof. By this, we can reduce the number of read operations.
Merkle root history
Because we save only confirmed node, you can get any merkle root history even if you don’t save them.
As we can see \mathbf{A} in proof, we know when nodes appended. If there are N leaf nodes but you want to know merkle root when there were K nodes, you just query with regarding confirmed nodes (which are inserted when K+1 ~ N leaf nodes inserted) as unconfirmed nodes.
Caching merkle roots for every append
Even though you can get any merkle root histories, you can cache them for every append by getting them with O(1). However, it makes append O(logn) complexity, same as original merkle tree.
Though, it’s more efficient if read operation is much cheaper than write operation (logn read operation costs < logn write operation costs). I tested in EVM smart contract and it costs less gas fee than original merkle tree.