MEV: Scalable fair-ordered DAG Mempool (DAGPool)

[chiro-hiro]

1. Abstract

We introduce DAGPool - a new DAG mempool protocol that leverages the gossip-DAG data structure to achieve scalability, order fairness, and censorship-resistant.

2. Objectives

• Achieve transaction order fairness through FIFO with ranked voting
• Provide censorship resistance
• Enhance scalability of Ethereum
• A practical solution compatible with existing blockchain networks

3. Overview

Ethereum, the leading programmable blockchain, currently faces critical issues: MEV exploitation undermining fairness, limited scalability (~14 TPS), long finality times (~2 epochs ~13 minutes), and rising censorship risks due to centralized block builders. In DAGPool, we mainly focus on the MEV, censorship and scalability problems.

3.1. MEV and Censorship Problems

MEV refers to value extracted by manipulating transaction order, including reordering, inserting, or censoring transactions. It manifests as front-running, sandwich attacks, arbitrage, and liquidation manipulation, exacerbated by fee markets. Proposer-Builder Separation (PBS) solutions like MEV-Boost and EIP-7732 aim to address this but remain vulnerable to centralization and censorship because parties can join as both of proposers and builders. Censorship risks are evident, builders may censor transactions for various reasons beyond regulatory compliance, such as maximizing MEV profits, blocking competitors’ trades, or enforcing private order flow agreements. With two builders (Titan and beaverbuild) controlling over 97% of block production, such censorship risks undermine Ethereum’s neutrality and decentralization.

3.2. Scalability

Ethereum’s current single-chain architecture has throughput of ~14 TPS and finality time of ~13 minutes (2 epochs) in the thrive of supporting more than 1 million validators. The fee market further delays low-fee transaction inclusion up to days, impacting decentralization. Previously, Ethereum community worked on the sharding approach with the hope of improving the scalability but now switch to the rollup-centric approach. However, the need of increasing throughput for Ethereum is still important.

Above challenges are central to Ethereum’s future, as highlighted in The Scourge roadmap, with no fully working solution yet.

3.3. Order fairness on a DAG: A Potential Solution to MEV, censorship and scalability problems at one

The problem of MEV originates mainly from the problem of unfair transaction ordering, which is formulated as the order fairness problem. Academic research focuses on order fairness mechanisms:

• FIFO-based solutions with ranked voting (transaction dependency preference graphs aggregation) (Aequitas, Themis, Rashnu, KLS24)
• FIFO with synchronized timestamps (Pompe, Lyra)
• Encrypted mempools using threshold decryption (CGPP24, BEAT-MEV), blind-order-fairness (Fino, AACY23)

Amongst these, FIFO with ranked voting is the most intuitive and have strong theoretical foundation but they are not integrated much in DLTs and only noticed recently in the literature. We observe that \gamma-batch order fairness notion of Themis is the most practical one based on FIFO-with-ranked-voting that provides O(T^2) time complexity where T is the number of transactions to be ordered. The other approaches are either impractical (exponential complexity) or proven vulnerable to attacks (KLS24).

Regarding scalability, DAG-based protocols, such as Narwhal & Tusk, Bullshark, Mysticeti, Hashgraph, and Tangle, offer high-throughput scalability and resilience in asynchronous environments, which show a great potential to improve the scalability of Ethereum compared to existing linear-chain-based protocols. However, while these protocols excel at preserving non-linear transaction dependencies, they lack a robust order fairness scheme compatible with DAG structures. The above mentioned works in order fairness provide theoretical foundations on order fairness algorithms but fall short of delivering a fully-fledged DAG protocol.

We also notice that, with careful design, a DAG protocol can efficiently provide censorship resistance besides order fairness.

We address this gap by introducing DAGPool, a novel DAG mempool protocol integrated with a FIFO-with-ranked-voting order fairness notion. DAGPool combines scalability of DAG with the \gamma-batch order fairness model adapted from Themis, ensuring transaction order fairness and censorship resistance. Also it is compatible with state-machine replication protocol like Ethereum. Inspired by the fork-tolerant gossip-DAG structure of Hashgraph which is later formalized in Cra21, DAGPool replaces its time-based consensus with a leader-based approach that natively supports our order fairness algorithm, offering censorship resistance, scalability, fault tolerance, and liveness under asynchrony.

3.4. The fault-tolerant gossip-DAG data structure

The gossip-DAG data structure, as presented in Cra21, operates in a network of n peers where more than two-thirds (> \frac{2n}{3}) are honest. The structure provides fork tolerance through an elegant self-fork dissolution mechanism.

3.4.1. Core Structure and Settings

The gossip-DAG consists of nodes which are gossip events created through peer communication, where each event contains:

• \text{selfParent}: Latest event by the same peer
• \text{crossParent}: Latest received event from another peer
• \text{newTxsList}: New transactions from clients and cross-parent ancestry that the creator of the node has not seen before
• \text{metadata}: Additional information related to consensus (batch proposals, voting data)
• \text{creatorSignature}: Creator’s signature for integrity verification

Since each new node refers to its self-parent, each peer maintains a node sequence of nodes created by it.

Events are organized into asynchronous rounds, with the first event of each peer in a round called a witness. For peer p_i at round r, its witness is denoted as w_{p_i, r}.

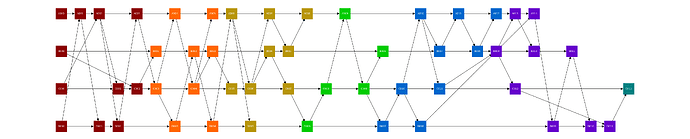
Figure 1: Example of a gossip-DAG
network with n = 4 peers (A, B, C, D) from the local view of peer B,
where the nodes in the same round are in the same color

3.4.2. Fork Types and Tolerance Properties

Two distinct types of forks are defined:

• Self-forks: When a peer creates two events in its node sequence where neither is the ancestor of the other
• State-forks: Conflicting candidates for the canonical common state (e.g. order of transaction, state of the common machine as in Bitcoin, Ethereum, …)

Key mathematical relations from Cra21:

1. Ancestor (x \lt y or x \leq y): Event x is a (strict) ancestor of y
2. Self-ancestor (x \sqsubset y or x \sqsubseteq y): (Strict) Ancestry via self-parent edges only
3. See (y \unlhd x): if x \leq y with no self-forks between them
4. Strongly see (y \ll x): if x is seen by a supermajority set Z of events, all ancestors of y. Here a supermajority set is a set of events that are created by more than two-thirds of the peers.

The unsee mechanism is implemented through the seeing property:

• When an event detects a self-fork, it blacklists/unsees all events from the forking peer from the equivocation point. Which means the nodes that sees the self-forking events are defined to not see them and all their descendants.
• This ensures only one side of a self-fork can be strongly seen, as proven in Lemma 2.3, [Cra21]

The structure achieves self-fork tolerance through this mechanism, allowing the network to focus primarily on resolving state-forks for consensus. When we refer to “fork-choice rule”, we specifically mean the rule for determining which state-fork should become canonical.

4. The DAGPool architecture

The goal of DAGPool is to construct a new mempool protocol that solves Ethereum’s problems in order fairness, censorship resistance, scalability, and latency while still comply with the decentralization principles. The DAGPool protocol is designed by integrating the underlying gossip-DAG structure with our new suite of protocol for consensus and order fairness on top of it. The core idea is to form batches of causually related nodes in the gossip-DAG and pseudorandomly select a leader to propose such a batch each round along with zk proofs of order fairness for the batch. The rest of the protocol is dedicated to achieving consensus on the network state which is a chain of these leader batches.

4.1 Settings and Notations

Let \mathcal{N} be the set of n peers in the network where n \geq 3f+1 and f is the number of Byzantine peers. Each peer p_i (0 \leq i < n) maintains its own hashchain E_{p_i} = \{e_{p_i,1}, e_{p_i,2}, \dots\} where each e_{p_i,j} represents the j_{th} event in the hashchain of peer p_i. We write e.\mathrm{round} when we refer to the round number of an event e.

The network also sets a common \gamma parameter (\frac{1}{2} < \gamma < 1) which is the minimum ratio of peers that accepts a relation between two transactions in a batch. This parameter will be used in the fair ordering algorithm.

4.2. Batch-by-batch network progression

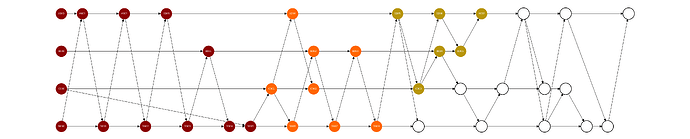
The network maintains a common state that captures the processed part of the gossip-DAG which the network participants work to achieve agreement on. The network progresses batch by batch, in which each batch represents the newly processed part of the gossip-DAG and it is represented by the head node of the batch. The head node of the latest processed batch is denoted as \text{head}_{\text{last}}. \text{head}_{\text{last}} represents the fully processed part of the gossip-DAG, in which all of its ancestors have been propagated and reviewed by a supermajority of peers, with most of them eventually sequenced and stored in the agreed network state. This ancestry part is the left cone of \text{head}_{\text{last}}.

Figure 2: The left cone of node A007 in the network state

Each time the network state is expanded, a new batch of unprocessed events is gathered from the gossip-DAG and sequenced if they are eligible by specific rules, which results in a new head of the network. Importanly, each batch focuses mainly on a round that has never been processed in previous batches, which we call the right sequence round of the batch, which is exactly 2 rounds before the round of the head node of the batch. By focusing we mean that a large portion of the events in the right sequence round are included in the batch and these events together constitue a supermajor set. Unprocessed events in previous rounds (up to 2 rounds before the right sequence round) are also included in the batch. The leftmost such round is called the left sequence round of the batch. We also have the definition of the right boundary of the batch, which is the supermajor set of witnesses of round r+1 that the head node strongly sees - this set exists due to the definition of witness.

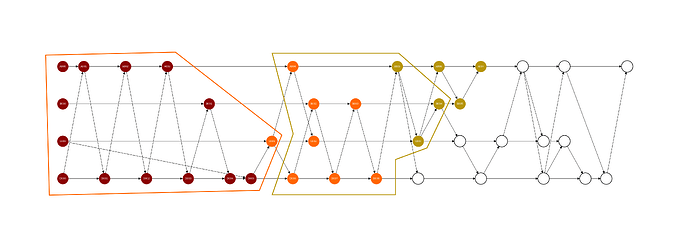
Figure 3: The orange-bordered region and the dark-yellow-bordered region represent the truncated cones of head nodes C001 and B001, respectively. Each truncated cone represents a batch and the corresponding leader runs the order fairness agorithm on the transactions of each truncated cone to achieve the fair transaction order

The batch is restricted to include and process all the unprocessed transactions in the region of events from the left sequence round to the right sequence round that the witnesses in the right boundary of the batch can see. This region of events is called the truncated cone of the batch, because it’s constructed by truncating the left and the right side of a part of the left cone of the head node. Notice that this notion of batch is different from round, in which each batch can contain unprocessed events from multiple adjacent rounds and it’s not allowed to touch the left cone the previous head. Now, we formally define the network state to contain the following information at any time:

• Processed Batches \{ b_0, b_1, \dots, b_{\text{last}} \}, where b_{\text{last}} is the latest processed batch. Each batch b_k consists of:
  • \text{id}_k: the id of the batch
  • \text{prevBlockId}_k: the id of the previous block in the batch
  • \text{head}_k: the k-th network head node in the batch
  • \text{rightBoundary}_k: the right boundary of \text{head}_k, which is the supermajor set of witnesses of round r+1 that \text{head}_k strongly sees
  • \text{rightSeqRound}_k: the right sequence round number of \text{head}_k, defined as
    \text{rightSeqRound}_k = \text{head}_k.\text{round} - 2
  • \text{leftSeqRound}_k: the left sequence round number of \text{head}_k, defined as
    \text{leftSeqRound}_k \geq \text{rightSeqRound}_k - 2
  • \text{seqTxsList}_k: the list of transactions sequenced fairly in batch b_k
  • \text{seqEvents}_k: the list of events sequenced in batch b_k. Specifically, \text{seqEvents}_k contains all the unsequenced events from \text{leftSeqRound}_k to \text{rightSeqRound}_k which forms the truncated cone of b_k
• If the network operates as a DLT rather than just a mempool layer, the state additionally includes the ledger state and any relevant data needed for consensus and transaction finality.

The peers work toward agreement on the network state batch by batch in an asynchronous process. In good network conditions, it is expected to have one batch per round. For a mempool, the network state primarily consists of the batches’ information, while for DLT, it also includes the ledger state. Although the network is expected to progress sequentially per round, it can “jump” between non-consecutive rounds—meaning two consecutive heads don’t necessarily belong to adjacent rounds. Since the cone can span up to 3 rounds, any missed events and transactions in previous rounds can have a chance to be captured and sequenced in up to three rounds. Transactions coming later than this are ignored so clients can resubmit them instead of waiting for a chance of inclusion that may never happen. This expiration mechanism is a new property that Ethereum doesn’t natively support. The specific number of rounds of spanning the truncated cone can be adjusted adaptively in practice. This design combined with the consensus protocol described later in section 3.2, provides liveness, fault tolerance while maintaining order fairness.

4.3. Leader-based transaction sequencing

For each round r, a leader l_r is deterministically selected (e.g., using a randomness beacon like Ethereum’s RANDAO). The leader’s role is to propose a batch \text{pb}_r expands a previous batch that the leader thinks is the last batch in the network state, b_{last}. The proposed batch \text{pb}_r sequences transactions fairly from the truncated cone of the batch.

Leader’s choice of head node and truncated cone

The leader first chooses the head node of the batch, denoted as w_{l_r, r+2} - the witness of l_r in round r+2 - which we call the anchor witness of round r+2 to distinguish it from the normal witnesses that carries no batch information. After determining the anchor witness (i.e. having a candidate pair of self-parent and cross-parent that together can form a witness of round r+2), the leader then determines the truncated cone of the batch.

1. Selecting the head node: w_{l_r, r+2}

• The leader l_r must advance to round r + 2 and get the self-parent and cross-parent that can be used to construct the anchor witness w_{l_r, r+2}, the leader computes the witness but does not propagate it immediately. Instead, it chooses and compute a batch \text{pb}_r with w_{l_r, r+2} as the head node and include the output in the witness data before propagating it to propose the batch. So this witness event is a special type of witness that carries the batch information.
• This witness strongly sees a supermajor set of (round r+1)-witnesses, forming the right-boundary of round r in this batch, denoted as \mathrm{RightBoundary}_{\text{pb}_r}, where |\mathrm{RightBoundary}_{\text{pb}_r}| \gt \frac{2}{3} |\mathcal{N}|.

2. Constructing the Truncated Cone \mathcal{T}_{\text{pb}_r}

• The leader chooses the left sequence round of the batch as \text{Max(r - 2, 0)} and the right sequence round of the batch as r.
• The truncated cone \mathcal{T}_{\text{pb}_r} includes all unsequenced events in rounds from the left sequence round to the right sequence round that are seen by one of events in the right boundary of the batch:
  \mathcal{T}_{\text{pb}_r} = \{ e \mid e.\text{round} \in [\text{leftSeqRound}_{\text{pb}_r}, \text{rightSeqRound}_{\text{pb}_r}] \wedge (\exists w \mid w \in \mathrm{RightBoundary}_{\text{pb}_r} \text{ s.t. } e \unlhd w) \}

Leader’s construction of input preference graphs

Next, the leader constructs the preference graphs from the truncated cone. Let C be set of creators of events in the truncated cone: C = \{ e.\text{creator} \mid e \in \mathcal{T}_{\text{pb}_r} \}. Let m = |C| be the number of creators in the truncated cone. We have m > 2/3 \cdot |\mathcal{N}| since the truncated cone contains a supermajor set of events. For each of the creator c_i \in C, the leader constructs a preference graph \mathcal{PG}_{c_i} as follows:

• Nodes represent transactions from events in the truncated cone whose creator is c_i. If some transactions are already sequenced in the previous batches, it is excluded from all the preference graphs.
• Edges represent the local preference relation of creator c_i between transactions:
  1. Self-parent dependency: If event e and its self-parent e' are both in the truncated cone, then add a new directed edge:
     (e.\mathrm{newTxList}_{\text{last}} \rightarrow e'.\mathrm{newTxList}_{\text{first}})
  2. Intra-event dependency: Transactions inside the same event maintain their natural order. These directed edges are added to the preference graph:
     (e.\mathrm{newTxList}_i \rightarrow e.\mathrm{newTxList}_{i+1}), \quad \forall i

This results are m preference DAGs \mathcal{PG}_{c_1}, \dots, \mathcal{PG}_{c_m}.

Fair ordering algorithm on preference graphs

In this step, the leader aggregate the m preference graphs to construct a final dependency graph \mathcal{G} and run the fair ordering algorithm of the \gamma-batch order fairness notion adapted from Themis, Sec 4.1.

For a preference graph \mathcal{PG}_{c_i}, if there is a path from \mathrm{tx}_1 to \mathrm{tx}_2 in \mathcal{PG}_{c_i} then we write \mathrm{tx}_1 \prec \mathrm{tx}_2 in \mathcal{PG}_{c_i}, which represents the local preference relation of creator c_i of the two transactions. Similary, we write \mathcal{tx}_1 \prec_{\gamma} \mathcal{tx}_2 if \mathrm{tx}_1 \prec \mathrm{tx}_2 in \gamma fraction of \mathcal{PG}_{c_i}.

The leader constructs the final dependency graph \mathcal{G} as follows:

• For each two transactions \mathrm{tx}_1 and \mathrm{tx}_2, we add a directed edge (\mathrm{tx}_1 \rightarrow \mathrm{tx}_2) if all these conditions satisfy:
  • \mathrm{tx}_1 \prec_{k_1} \mathrm{tx}_2
  • \mathrm{tx}_2 \prec_{k_2} \mathrm{tx}_1
  • k_1 > max(k_2, \gamma)

Since there are at most two edges between any two transactions, \mathcal{G} is a tournament graph.

The fair ordering is then applied on this final dependency graph \mathcal{G} to produce the final order of transactions in the batch. To do this, the leader first find the DAG of strongly connected components in \mathcal{G} and then topologically sort the SCC DAG. For each SCC, the leader finds the Hamilton cycle and rotates it to put the transaction with the largest weight first. The weight of a transaction is calculated as the number of peers that have seen it. Note that all strongly connected tournaments contain a Hamiltonian cycle and finding a Hamiltonian cycle on a tournament takes linear time in the number of edges (Man92).

def fair_ordering(G, peers):
    """
    Perform fair ordering by processing the SCC DAG topologically and rotating
    the Hamilton cycle in each SCC based on transaction weight.
    """
    scc_DAG = G.find_scc_DAG()  # Find the DAG of strongly connected components in G
    sccs_topo = scc_DAG.topological_sort()  # Topological sort for the SCC DAG
    final_order = []

    for scc in sccs_topo:
        hamilton_cycle = scc.find_hamilton_cycle()  # Find the Hamilton cycle in the SCC

        # Find the transaction with the largest weight
        max_weight = -oo
        max_weight_tx_pos = 0

        for i, tx in enumerate(hamilton_cycle):
            weight = tx.weight()
            if weight > max_weight:
                max_weight = weight
                max_weight_tx_pos = i

        # Rotate the Hamilton cycle to put the max-weight transaction first
        rotated_hamilton_cycle = hamilton_cycle[max_weight_tx_pos:] + hamilton_cycle[:max_weight_tx_pos]

        final_order.extend(rotated_hamilton_cycle)

    return final_order

This algorithm runs in O(V + E) time where V is the number of vertices and E is the number of edges in \mathcal{G}. The verification process of this algorithm also takes linear time complexity.

Finalizing the batch and propagation

After sequencing the transactions, the leader constructs the batch \text{pb}_r as follows:

• Previous Batch Id \text{prevBlockId}_{\text{pb}_r}
• head node w_{l_r, r+2}
• Right and Left Sequence Rounds (\text{rightSeqRound}_{\text{pb}_r}, \text{leftSeqRound}_{\text{pb}_r})
• Sequenced Transactions \text{seqTxsList}_{\text{pb}_r} from \mathcal{G}_{\text{pb}_r}, which is the output of \mathrm{fair\_ordering}(\mathcal{G}) function
• Sequenced Events \text{seqEvents}_{\text{pb}_r} forming \mathcal{T}_{\text{pb}_r}
• Batch Id \text{id}_{\text{pb}_r} is computed as the hash of the batch information

The hash id of witness event w_{l_r, r+2} is recomputed with the \text{pb}_r information included in its \text{metadata} field. Then the leader gossips w_{l_r, r+2} as a witness of round r+2 using the normal gossip-of-gossip mechanism. Here the gossiped witness event w_{l_r, r+2} must indeed be a witness of round r+2, unless it’s deemed invalid by the network due to containing the batch information, which is not allowed.

Only the leader can gossip a witness event carrying a batch at the specified position (witness of round r+2 for a batch with right sequence round r), otherwise the creator of the event will be penalized by the network.

Next, the network run the consensus protocol to achieve agreement on the validity of the batch and hence the network state. We leave it as a black-box construction for now. Some reference constructions of consensus protocol on a DAG such as Narwhal & Tusk, Bullshark, Mysticeti, Hashgraph, Tangle, … Most of them can be apply for this leader-based gossip-DAG architecture. For a rough estimation, we estimate that it takes 3 - 4 rounds for the network to reach agreement, as in the usual DAG networks. More initiatives can be done to improve the consensus protocol to achieve faster finality.

Extending to DLT

If the network operates as a DLT, besides sequencing the truncated cone of the batch, the leader also executes the VM computation on the sequenced transactions and includes the updated ledger state in the batch. The same consensus protocol is applied as in the mempool-only case.

5. Discussion

We summarize the pros and cons of DAGPool and the further considerations in this section.

Pros of DAGPool

• MEV resistance: Leverages a gossip-DAG structure to preserve the natural propagation order of transactions, ensuring fairness via a \gamma-batch order fairness model
• Censorship resistance: The gossip-DAG structure ensures censorship resistance because a round leader cannot ignore transactions in the truncated cone
• Scalability: The DAG structure enables hyper-throughput as in exisiting DAG-based protocols, with unlimited scaling potential

Cons of DAGPool

• Large validator sets: Scaling to a large number of validators requires careful economic and consensus design, especially for a large number of validators (> 1 million) as in Ethereum
• Flooding attacks: Peers may deliberately send excessive gossip events to disrupt the preservation of propagation order, we can impose some restrictions to limit the number of less meaningful gossip events being recorded in the gossip-DAG
• Implementation complexity: The system’s sophisticated design introduces challenges in implementation and migration from existing systems.

Further Considerations and Future Directions

While DAGPool provides a strong foundation for scalable and fair consensus, several challenges and research opportunities remain crucial for its future development:

• Enhancing Order Fairness: Developing a new theoretical framework for order fairness, potentially leveraging dissemination patterns to improve transaction ordering in DAG-based systems.
• Scalability with Large Validator Sets: Supporting a vast number of validators (e.g., >1 million) poses technical challenges, particularly in vote aggregation. Solutions such as fast-path processing for isolated transactions could help enhance throughput.
• Decentralization: Maintaining both accessibility and performance requires careful design choices, including validator stake capping, hardware requirements, and smooth validator rotations at epoch boundaries.
• Economic and Security Considerations: Refining incentive mechanisms and slashing conditions to ensure long-term network security and sustained participation.
• Migration Strategies: Establishing clear transition pathways from existing systems like Ethereum to facilitate adoption.
• Active Voting Protocols: Designing efficient active voting protocols using lightweight updatable accumulators to enable broader participation in network security without overburdening the system. Techniques such as PCD (Proof-Carrying Data) or IVC (Incrementally Verifiable Computation) could allow smaller validators to contribute meaningfully while maintaining protocol efficiency.
• SNARK-Based Consensus Layer: Fully integrating SNARKs into the consensus layer could significantly enhance scalability and security.
• Attack Mitigation: Addressing flooding attacks—where a peer floods the network with excessive vertices—while ensuring robust recursive voting mechanisms to maintain network integrity.
• Benchmarking DAG-Based Systems: Establishing standardized benchmarks for evaluating order fairness in DAG-based consensus mechanisms (e.g., Shoal(++), Cordial Miners, etc.).

By tackling these challenges and advancing research in these areas, DAGPool can evolve into a highly scalable, fair, and decentralized consensus mechanism that balances efficiency, security, and inclusivity.

Thanks,
DAGPool Team

[meridian]

define “order fairness” please

[chiro-hiro]

We want to prove the mempool as it is, first come, first served.