More Viable Plasma

[kfichter]

Authors: Ben Jones, Kelvin Fichter

And a very special thank you to vi, Li Xuanji, David Knott, Eva Beylin, Vitalik Buterin, and Kasima Tharnpipitchai for invaluable contributions to putting this together.

---

TL;DR

We propose an alternative to confirmation signatures and (semi) formalize the properties of any valid Plasma MVP exit game. Our game provides significantly improved UX at the cost of a two-period challenge-response scheme in the worst case.

Background

Exit Priority

The original Plasma MVP specification requires that exits be processed in priority order. Each exit references an unspent transaction output, and priority is determined by the age of the transaction output. This is generally necessary so that valid exits can be processed before exits stemming from invalid “out of nowhere” transactions. More information about exit priority can be found at the OmiseGO research repository here.

This post introduces a new way to calculate exit priority, which we call “youngest-input” priority. Instead of ordering exits by the age of the output, we now order exits by the age of the youngest input. This has the effect that exits of outputs, even if they’re included in withheld blocks after “out of nowhere” transactions, will be correctly processed as long as they only stem from valid inputs.

Exit Game

Plasma MVP also introduces an exit game, whereby some outputs are deemed “exitable”. This game correctly incentivizes parties to challenge a “non-exitable” output. For example, spent outputs are considered “non-exitable.” The game requires the exitor to place a bond, such that anyone who knows the output to be spent is sufficiently incentivized to reveal the transaction and take the bond.

The basic exit game has one challenge condition - outputs must not be spent. This condition is enough to make the exit game complete because of a construction of confirmation signatures. Basically, both parties to a transaction must “sign off” on a transaction’s inclusion in the chain. Honest clients won’t sign off on withheld (and therefore possibly invalid) transactions, so honest clients won’t accept funds that might be stolen by the operator (discussed more below).

In-flight Transactions

Without confirmation signatures, the above exit game is exploitable by the operator in two ways:

1. The operator may include, but withhold, a transaction, and later grief the sender(s) by challenging exits from the transaction’s inputs.
2. More importantly, the operator may include a transaction after some invalid “out of nowhere” transaction that creates money for the operator. Standard exit priority dictates that the operator’s outputs will be processed before the valid outputs, thereby stealing money.

Our new exit game solves these problems without confirmation signatures.

Youngest-Input Priority

This proposal replaces output-age priority with something we call “youngest-input” priority. Basically, the exit priority of an output is now the age of its youngest input. We claim that this construction is safe (honest clients cannot have money stolen) as long as clients don’t spend any outputs included after any invalid or witheld transaction.

We show that if there exists an “out of nowhere” input, then any transactions stemming from that input would have an even higher queue number than the “out of nowhere” itself. Therefore, valid outputs will be processed first.

Safety Proof

We begin with definitions to be used throughout this post.

TX is the transaction space, of the form (inputs, outputs), where inputs and outputs are sets of integers representing position in the Plasma chain:

TX: ((I_{1}, I_{2}, \ldots, I_{n}), (O_{1}, O_{2}, \ldots, O_{m}))

For all t \in TX, we define the “inputs” function I(t)=(I_{1}, I_{2}, \ldots, I_{n}) and the “outputs” function O(t)=(O_{1}, O_{2}, \ldots, O_{n}).

Transactions have older inputs than outputs, more formally:

\max(I(t)) < \min(O(t))

We also define the mapping T_{n} which maps a Plasma chain’s first n transaction indices to its first n transactions.

T_{n}: (0, n] \rightarrow TX

As a shortcut,

t_{i} = T_{n}(i)

We define the priority number (“lower exits first”, “lower is better”) of a transaction, p(t), as:

p(t) = \max(I(t))

We say that a transaction t_{k} stems from a transaction t_{j} (an output from t_{j} eventually chains into an input of t_{k}) if the following holds:

stems\_from(t_{j}, t_{k}) = (O(t_{j}) \cap I(t_{k}) \neq \varnothing) \vee (\exists t : stems\_from(t_{j}, t) \wedge stems\_from(t, t_{k}))

A transaction t_{i} with n inputs is considered an “out of nowhere” transaction if any input “points to itself”:

\exists j \in [0, n): I(t_{i})_{j} = \max(O(t_{i-1})) + j

This is how deposits are structured, so it’s like a deposit that never happened - creating money “out of nowhere”.

Let t_{v} be some transaction and t_{nw} be an out of nowhere transaction such that, from our previous definition:

\max(I(t_{v})) < \max(I(t_{nw}))

and therefore by our definition of p(t):

p(t_{v}) < p(t_{nw})

So p(t_{v}) will exit before p(t_{nw}). We now need to show that for any t' that stems from t_{nw}, p(t_{v}) < p(t') as well. Because t' stems from t_{nw}, we know that:

(O(t_{nw}) \cap I(t') \neq \varnothing) \vee (\exists t : stems\_from(t_{nw}, t) \wedge stems\_from(t, t'))

If the first is true, then we can show p(t_{nw}) < p(t'):

p(t') = \max(I(t')) \geq \max(I(t') \cap O(t_{nw})) \geq \min(O(t_{nw})) > \max(I(t_{nw})) = p(t_{nw})

Otherwise, there’s a chain of transactions from p_{nw} to p' for which the first is true, and therefore the inequality holds by transitivity.

So basically, anyone following the protocol can exit before anything that stems from an “out of nowhere” transaction.

Required Exit Game Properties

Our exit game defines a set of “exitable outputs” given a transaction t. For example, spent outputs are not exitable in our rules. We formally define the properties that this game must satisfy. We call these properties “safety” and “liveness”, because they’re largely analogous.

Safety

The safety rule, in English, says “if an output was exitable at some time and is not spent in a later transaction, then it must still be exitable”. If we didn’t have this condition, then it might be possible for a user to receive money but not be able to spend or exit from it later.

Formally, if we say that E(T_{n}) represents the set of exitable outputs for some Plasma chain and T_{n+1} is T_{n} plus some new transaction t_{n+1}:

\forall o \in E(T_{n}) : o \not\in I(t_{n+1}) \implies o \in E(T_{n+1})

Liveness

The liveness rule basically says that “if an output was exitable at some time and is spent later, then immediately after that spend, either it’s still exitable or all of the spend’s outputs are exitable, but not both”.

The second part probably makes sense - if something is spent, then all the resulting outputs should be exitable. The first case is special - if the spend is invalid, then the outputs should not be exitable and the input should still be exitable. So a short way to describe “liveness” is that all “canonical” transactions should impact the set of exitable transactions.

We define “canonical” later.

Formally:

\forall o \in E(T_{n}), o \in I(t_{n+1}) \implies o \in E(T_{n+1}) \oplus O(t_{m+1}) \subseteq E(T_{n+1})

Proof

Exit Game Requirements

We need to formally show our exit game produces the exitable outputs E. To help us along the way, we make a few useful definitions.

Spends

We call two transactions “competing” if they contain any of the same inputs. The list of “competitors” to a transaction is formally defined as follows:

competitors(t) = \{ t_{i} : i \in (0, n], I(t_{i}) \cap I(t) \neq \varnothing \}

Note that a transaction is a competitor to itself.

Canonical Transactions

We call a transaction “canonical” if it’s the first included of any of its competitors.

We define a function that determines which of a set T of transactions came “first”:

first(T) = t \in T : \forall t' \in T, t \neq t', min(O(t)) < min(O(t'))

Then we can define a function that takes a transaction and returns whether it’s the “canonical” spend in its set of competitors.

canonical: TX \rightarrow bool

canonical(t) = (first(competitors(t)) \stackrel{?}{=} t)

Finally, we say that “reality” is the set of canonical transactions for a given Plasma chain.

reality(T_{n}) = \{ canonical(t_{i}) : i \in (0, n]\}

Unspent, Double Spent

We define two helper functions “unspent” and “double spent”. unspent takes a set of transactions and returns the list of outputs that haven’t been spent. double\_spent takes a list of transactions and returns any outputs that have been used as inputs to more than one transaction.

First, we define a function txo that takes a transaction and returns a list of its inputs and outputs.

txo(t) = O(t) \cup I(t)

Next, we define a function TXO that lists all inputs and outputs for an entire set of transactions:

TXO(T_{n}) = \bigcup_{i = 1}^{n} txo(t_{i})

Now we can define unspent:

unspent(T) = \{ o \in TXO(T) : \forall t \in T, o \not\in I(t) \}

And finally, double\_spent:

double\_spent(T) = \{ o \in TXO(T) : \exists t,t' \in T, t \neq t', o \in I(t) \wedge o \in I(t') \}

Requirements

Combining all of these things, we define our function for exitable outputs given a set of transactions, E, as:

E(T_{n}) = unspent(reality(T_{n})) \setminus double\_spent(T_{n})

Basically, the set of exitable outputs are the outputs that are part of a canonical transaction, are unspent, and were not spent in two or more non-canonical transactions. This last part effectively punishes users for double spending.

Satisfies Properties

This next section demonstrates that the function described above satisfies the desired properties of safety and liveness.

Safety

Our safety property says:

\forall o \in E(T_{n}), o \not\in I(t_{n+1}) \implies o \in E(T_{n+1})

So to prove this for our E(T_{n}), let’s take some o \in E(T_{n}). From our definition, o must be in unspent(reality(T_{n})), and must not be in double\_spent(T_{n}).

o \not\in I(t_{n+1}) means that o will still be in reality, because only a transaction spending o can impact its inclusion in reality. Also, o can’t be spent (or double spent) if it wasn’t used as an input. So our function is safe!

Liveness

Our liveness property states:

\forall o \in E(T_{n}), o \in I(t_{n+1}) \implies o \in E(T_{n+1}) \oplus O(t_{n+1}) \subseteq E(T_{n+1})

However, we do have a case for which liveness does not hold - namely that if the second transaction is a non-canonical double spend, then both the input and all of the outputs will not be exitable. This is a result of the \setminus double\_spent(T_{n}) clause. We think this is fine, because it means that only double spent inputs are at risk of being “lost”.

The updated property is therefore:

\forall o \in E(T_{n}), o \in I(t_{n+1}) \implies o \in E(T_{n+1}) \oplus O(t_{n+1}) \subseteq E(T_{n+1}) \oplus o \in double\_spent(T_{n+1})

This is more annoying to prove, because we need to show each implication holds separately, but not together. Basically, given \forall o \in E(T_{n}), o \in I(t_{n+1}), we need:

o \in E(T_{n+1}) \implies O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \wedge o \not\in double\_spent(T_{n+1})

and

O(t_{n+1}) \subseteq E(T_{n+1}) \implies o \not\in E(T_{n+1}) \wedge o \not\in double\_spent(T_{n+1})

and

o \in double\_spent(T_{n+1}) \implies O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \wedge o \not\in E(T_{n+1})

Let’s show the first. o \in I(t_{n+1}) means o was spent in t_{n+1}. However, o \in E(T_{n+1}) means that it’s unspent in any canonical transaction. Therefore, t_{n+1} cannot be a canonical transaction. O(t_{n+1}) \cap E(T_{n+1}) is empty if t_{n+1} is not canonical, so we’ve shown the half. Our specification states that o \in double\_spent(T_{n+1}) \implies o \not\in E(T_{n+1}), so we can show the second half by looking at the contrapositive of that statement o \in E(T_{n+1}) \implies o \not\in double\_spent(T_{n+1}).

Next, we’ll show the second statement. O(t_{n+1}) \subseteq E(T_{n+1}) implies that t_{n+1} is canonical. If t_{n+1} is canonical, and o is an input to t_{n+1}, then o is no longer unspent, and therefore o \not\in E(T_{n+1}). If t is canonical then there cannot exist another earlier spend of the input, so o \not\in double\_spent(T_{n+1}).

Now the third statement. o \in double\_spent(T_{n+1}) means t is necessarily not canonical, so we have O(t_{n+1}) \cap E(T_{n+1}) = \varnothing. It also means that o \not\in E(T_{n+1}) because of our \setminus double\_spent(T_{n}) clause.

Finally, we’ll show that at least one of these must be true. Let’s do a proof by contradiction. Assume the following:

O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \wedge o \not\in E(T_{n+1}) \wedge o \not\in double\_spent(T_{n+1})

We’ve already shown that:

o \in E(T_{n+1}) \implies O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \wedge o \not\in double\_spent(T_{n+1})

We can negate this statement to find:

o \not\in E(T_{n+1}) \wedge (O(t_{n+1}) \subseteq E(T_{n+1}) \vee o \in double\_spent(T_{n+1}))

However, we assumed that:

O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \wedge o \not\in double\_spent(T_{n+1})

Therefore we’ve shown the statement by contradiction.

Note that this means we should be careful to ensure that users don’t double spend. Imagine the following scenario:

1. Alice (UTXO1) and Bob (UTXO2) sign a transaction spending to Carol (TX1)
2. Bob (UTXO2) signs a transaction spending to Dan (TX2). This transaction is included first.
3. Alice (UTXO1) sees Bob’s transaction and signs a separate transaction spending to Carol (TX3).
4. The operator then includes TX1 and TX3. The chain is now byzantine and UTXO1 is also locked.

We can mitigate the above example by including timeouts on transactions. TX1 could have an n-block timeout, after which it’s treated like a totally invalid transaction that can’t be used to exit, challenge, or spend.

In-flight Exit Game

We have to construct a game which, given a transaction, returns any exitable inputs or outputs.

Construction

In the non-byzantine case, we can always use the standard exit game. However, in the event of invalid transactions or witheld blocks, we need to constuct a
“special exit”.

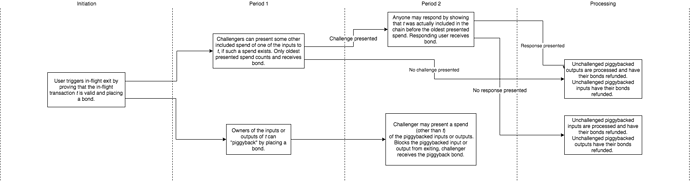
Our exit game involves two periods, triggered by a user who posts a bond alongside a transaction t. Note that any user (even someone who isn’t a party to the transaction) can start the exit process, but the parties must piggyback onto the transaction separately if they want to join this exit. The first period consists of the following:

1. Honest owners of inputs or outputs to t “piggyback” on this exit and post a bond. Users who do not piggyback will not be able to exit.
2. Any user may present any competitor to t.

Users who present a competitor (2.) must place a bond. Any other user may present an earlier competitor, claim the bond, and place a new bond. This construction ensures that the last presented competitor is also the earliest competitor.

If no competitors to t are brought to light, then the outputs can be challenged by an included spend. Any unchallenged outputs are exited. The bonds of all inputs and honest outputs are returned.

Otherwise, if competitors were presented, period 2 serves to determine whether t is canonical. Any user may present:

1. t, included in the chain before all competitors presented in period 1.
2. Spends of any “piggybacked” inputs or outputs (except t itself).
3. That some input was not created by a canonical transaction. This means revealing both the transaction that created the input, as well as some competitor to that transaction such that the competitor came first.

Challenges of type (2.) block any spent inputs or outputs to t from exiting. Challenges of type (3.) block any non-canonical inputs from exiting.

At the end of the game, only correctly exitable transactions will still be in the queue.

Justification

This construction essentially allows any input or output to exit if it satisfies the following conditions:

1. An earlier spend of one of its inputs does not exist.
2. A spend of it does not exist.
3. It has not been double spent (though note that if it has, the unspent outputs of the first canonical spend, if such a spend exists, are exitable separately).

(1.) is satisfied for t by the challenge-response game between periods 1 and 2, and for each of t's inputs by a type (3.) challenge in period 2.

Both (2.) and (3.) are satisfied by any type (2.) challenge in period 2.

In other words, the game determines if:

1. canonical(t)
2. o \in unspent(T_{n})
3. o \not\in double\_spent(T_{n})

If all of these are true, then:

o \in unspent(reality(T_{n})) \setminus double\_spent(T_{n}) = E(T_{n})

Otherwise, o \not\in E(T_{n}), which is the desired result.

Notes

Here’s a picture that attempts to illustrate the exit game:

If someone spots a mistake that causes this whole construction to be hopelessly broken, please let us know!

[colin-axner]

Very cool construction.

Regarding the youngest input age priority. What type of structure were you thinking for clearing such a queue? If priority is solely determined by the youngest input age, what occurs if exit for transaction A (with top priority currently) is nearing the end of its challenge periods, and then an exit for transaction B (with older inputs, lower priority) is submitted?

Then if processing the queue by taking the lowest priority and checking if its challenge period has ended would result in the delay of transaction A being processed despite it’s challenge period being over and transaction B’s challenge period just beginning.

[kfichter]

@colin-axner

What type of structure were you thinking for clearing such a queue?

I think the 7 day cutoff system from the original MVP spec covers this, i.e. exits have age min(youngest input, 7 days).

[josojo]

That is a great write-up. I could not find any issues with this construction.

This “more viable plasma” will not just make token-transfers of a plasma chain much easier, but getting rid of confirm transactions will also benefit many other applications of the plasma-technology.

E.g. plasma exchanges had always the problem that not the order taker, but the order placer had a “free option” to cancel the trade right after the trade was executed. This free option was needed, since during the trade a data unavailability could happen.
With this construction it should be able to allow people match an order from a orderbook with a transaction output older than the order transaction. Then, the trade can be settled with a priority of the youngest trade input. This would have the effect that the order placer knows that the priority of the trade is high enough to exit before any malicious behavior occurred and thereby we do not have to give him the “free option” to cancel the trade.

I really really like this construction of the more viable plasma!

[kfichter]

@josojo

plasma exchanges had always the problem that not the order taker, but the order placer had a “free option” to cancel the trade right after the trade was executed. This free option was needed, since during the trade a data unavailability could happen.

Yep! This is exactly one of the reasons why we wanted to get rid of confirmation signatures.

[colin-axner]

Yeah you are right, the 7 day cutoff system should work.

When a user begins an exit, I think they should not only provide transaction t, but merkle proofs for each of the inputs. Merkle proofs can be provided since you can assume the inputs are not under block withholding constraints. They are necessary to prove the correctness of a transaction.

For example, without proving inclusion of the inputs, I could create a transaction with input addresses B referencing inputs at block n, even though the actual inputs of block n belong to address A. In a similar fashion, I could also create a transaction giving me 100 ether even though the inputs in reality were worth only 10 eth. Instead of challenging with the correct input information, it is easier to verify the inclusion of the inputs that are being referenced.

[kfichter]

@colin-axner

When a user begins an exit, I think they should not only provide transaction t, but merkle proofs for each of the inputs.

My current implementation has the user submit all signatures for t upfront. Any other user can then reveal a transaction that created an input to t such that the revealed signature is invalid. It’s a little less gas than revealing the input transactions up front.

I think it’s also possible to have the user submit a sum merkle tree along with t so we can easily prove that the value of all the inputs is valid, need to double check.

But yep, we need to prove that t is valid - suggestions for other ways to do this are more than welcome

[MaxC]

@kfichter

even if they’re included in withheld blocks after “out of nowhere” transactions, will be correctly processed as long as they only stem from valid inputs.

I think you need to refine your construction. It is not safe or live as it is written.

[kfichter]

@MaxC

I think you need to refine your construction. It is not safe or live as it is written.

Can you explain what you mean? We define “valid” transactions as coming from available/valid blocks (maybe this definition is what makes it confusing). Then we know that the transaction either definitely spends valid inputs (only spends inputs created before invalid tx/data withholding), or possibly spends invalid inputs (data is withheld).

Maybe we should refine the definition to “available/valid” and “possibly invalid”:

Our scheme guarantees that any transaction stemming only from available/valid inputs will be processed before any transaction stemming from any possibly invalid inputs.

We impose a rule that honest clients will never spend (only exit) an output that’s received after data withholding or an invalid tx.

When someone exits via our game, they reveal a signed transaction that spends some inputs. If all of these inputs were created before withholding, then there’s no issue. If any input was created after withholding, then it must have priority of at most “after withholding”.

[MaxC]

Yeah, this scheme requires data availability to work. But with availability the exits should be relatively straightforward, as anyone can challenge false withdrawals and therefore save their coins from being stolen.

Seems to me a major problem with Plasma is that delegated exits when data is not available must be trusted. I don’t think confirmation signatures are the big problem…

[kfichter]

@MaxC

Yeah, this scheme requires data availability to work. But with availability the exits should be relatively straightforward, as anyone can challenge false withdrawals and therefore save their coins from being stolen.

The exit game specified is specifically designed not to require availability.

[MaxC]

The problem is how you define a competitor transaction. Suppose a transaction is in an unavailable block which withdraws more money than it should and references certain objects, which are distinct from mune. I have no idea whether those objects are valid or not, so I can’t challenge. This means someone can run away with the funds with an invalid transaction in an unavailable block.

[MaxC]

In your definition of the priority of a transaction, there is nothing to state that the transaction must come before mine, unless it is specifically ordered by block id as with the old Plasma MVP.

[kfichter]

@MaxC

I have no idea whether those objects are valid or not, so I can’t challenge. This means someone can run away with the funds with an invalid transaction in an unavailable block.

Correct, these transactions will still be able to exit. Our game just guarantees that any transactions stemming from inputs before an invalid tx or withholding will be able to exit before any transaction stemming from the “out of nowhere” output.

We’re basically not changing any of the assumptions of the original MVP, except that we remove the need for confirmation signatures.

[kfichter]

@MaxC

unless it is specifically ordered by block id as with the old Plasma MVP.

It’s still ordered by (block #, txindex) except we look at the (block #, txindex) of the youngest input to an output instead of the output itself.

[MaxC]

I see, nice work. Have you done any work on exits?

[kfichter]

@MaxC

Have you done any work on exits?

What sort of work do you mean?

[pdobacz]

Let’s look at the liveness proof (at “Our liveness property states…”), something isn’t clear for me there.

You’ve proven that if o \in I(t_{n+1}) then the two “implied components” of the XOR won’t happen at the same time. In fact you proved this twice, since the two statements:

o \in E(T_{n+1}) \implies O(t_{n+1}) \cap E(T_{n+1}) = \varnothing \implies O(t_{n+1}) \not\subseteq E(T_{n+1})

and

O(t_{n+1}) \subseteq E(T_{n+1}) \implies o \not\in E(T_{n+1})

are in contraposition, therefore equivalent.

However, the implication that at least one of the “implied XOR components” is true, provided o \in I(t_{n+1}) is still to be proven.

Maybe a way to prove would be to prove the contraposition of the whole thing, i.e.:

\forall o \in E(T_{n})
(o \in E(T_{n+1}) \land O(t_{n+1}) \subseteq E(T_{n+1})) \lor (o \not\in E(T_{n+1}) \land O(t_{n+1}) \not\subseteq E(T_{n+1})) \implies o \not\in I(t_{n+1})

but that seems not easily manipulable, I’m stuck here.

[benj0702]

If you’re willing to accept our proofs that both will not happen at once, then I think the guarantee of at least one happening just follows from canonical(t_{n+1}) \vee \neg canonical(t_{n+1}) \ , since each was used as an intermediate step in the proofs.

[kfichter]

There is a case where neither will happen (input is double spent, noted by \setminus DS(T_{n})). We need to update the original statement and proof to reflect this.

Non-breaking, but should be clarified.