Nakamoto Consensus with VDF and VRF

Proof-of-Stake
1

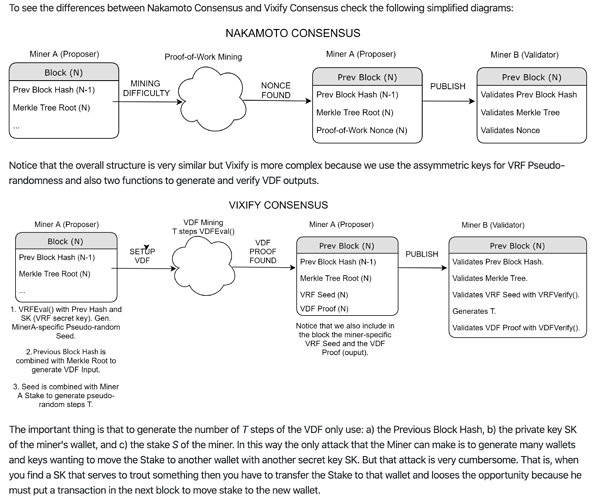
Hey guys, had some thoughts on combining the Nakamoto consensus with verifiable delay function (VDF) and verifiable random function (VRF).

The idea is to use VDF to simulate the PoW puzzle solving, and VRF to create puzzle difficulty variations for different validator nodes. Combining the VDF puzzle with the Nakamoto longest chain rule, validator nodes are effectively chosen at random as the block proposer for each block height. Compared to BFT based consensus which usually poses an upper limit on the number of validator nodes, this approach can achieve a high level of decentralization like Bitcoin, and yet does not burn nearly as much electricity for potentially the same level of security.

Here are the details. For block height i, the validator nodes compete to solve the following VDF puzzle. Whichever validator first solves the puzzle can extend the chain.

(r_i, \pi_i^r) \leftarrow VRF_{sk}(seed=d_{i-1} || r_{i-1})

(d_i, \pi_i^d) \leftarrow VDF(x=r_i, T=r_i / S)

Here sk is the secret key of the validator, and S is the stake (i.e., number of coins) of the validator. r_i and \pi_i^r are the random number and its corresponding proof generated by the VRF. Similarly, d_i and \pi_i^d are the output for the VDF function and its proof. These four strings, along with the public key of the block proposer, needs to be included in the block header for other validators to verify the correctness of the proposed block.

In the first formula, the VRF function uses the concatenation of d_{i-1} and r_{i-1} as the seed, where both of the two random numbers can be retrieved from the header of the parent block at height i - 1. The VRF returns r_i, which is used in the second formula to modulate the difficulty of the VDF puzzle. Thus, each validator node has to solve a puzzle with different difficulty (and hence takes different amount of time).

The second formula uses Pietrzak’s iterative squaring VDF construct, which takes two input parameters, x and the number of iterations T. We simply set x to r_i, and T to r_i/S. Note that T, and therefore the difficulty of the VDF puzzle is inversely proportional to the validator’s stake S. This can effectively prevent the sybil attack. A user can attempt to create multiple accounts, each with a fraction of his total stake, and solve the corresponding VDF puzzles in parallel. However, it can be proven using the expectation of the minimum of uniform random variables that by doing this, the expected amount of time to solve the VDF puzzle only increases. Thus, the best strategy is to put all the stake in a single account.

We also note that in the first formula, the concatenation d_{i-1} || r_{i-1} is used as the seed for the VRF. This is to prevent malicious users from quickly evaluating the difficulty for each branch if he wants to fork the chain.

Update:

Actually we can make the VDF puzzle even more similar to the PoW hashing puzzle. Still based on Pietrzak’s scheme, the VDF puzzle asks for integer T, such that

K(H(r_i)^{2^T}) < M

Here K() is a one-way hash function. Once T is found, the validator node also outputs d_i = H(r_i)^{2^T} , and the corresponding proof \pi_i^d. With the proof, other validators can very quickly verify that (1) d_i is indeed equal to H(r_i)^{2^T} , and (2) K(d_i )< M.

Such a VDF puzzle has the advantage that the validators don’t know how long it takes to obtain the solution until the solution is found. This is similar to the PoW hashing puzzle.

However, we note that this VDF puzzle is inherently sequential, so unlike the PoW hashing puzzle, throwing more hardware cannot shorten the solving time.

Also note that the random number r_i for different validator nodes are not the same. Hence, each validator is solving a different puzzle. And here is where the randomness/lottery comes from.

Thoughts? Any loophole in the proposal? Any feedback is appreciated!

2 Likes
2

Actually we can make the VDF puzzle even more similar to the PoW hashing puzzle. Still based on Pietrzak’s scheme, the VDF puzzle asks for integer T, such that

H(r_i)^{2^T} < M

Once T is found, the validator node also outputs d_i = H(r_i)^{2^T} , and the corresponding proof \pi_i^d. With the proof, other validators can very quickly verify that (1) d_i is indeed equal to H(r_i)^{2^T} , and (2) d_i < M.

Such a VDF puzzle has the advantage that the validators don’t know how long it takes to obtain the solution until the solution is found. This is similar to the PoW hashing puzzle.

However, we note that this VDF puzzle is inherently sequential, so unlike the PoW hashing puzzle, throwing more hardware cannot shorten the solving time.

Also note that the random number r_i for different validator nodes are not the same. Hence, each validator is solving a different puzzle.

4

will the speed of generating a block too slow?

5

if everybody has the same VDF device, would this make those with more stakes deterministicly win over those with less?

Would this encourage mining pools?

6

I guess we can tweak the difficulty of the VDF puzzle to control the block interval

7

Yes good point! The expected return can be higher if people form staking pools. For example, other things being equal, a validator with 2s stake is more likely to solve the VDF puzzle than two validators each having s stake within the same amount of time (since 2p > 1 - (1-p)^2). Hence it is more profitable to pool the stake together with the design described in the original post.

To address this I think we can place a cap on the max stake per validator node to make it more fair to all participants.

8

um, it will end up with all people with the “max stake”, so why not fix the staking amount? :smiley:

9

Hey,

Can you explain what’s exactly the purpose of the VDF in your scheme?
Why not just use a VRF (kind of like Algorand proposes)?

10

Yes possibly :slight_smile: That also simplifies the design. In practice though, it might be beneficial to have a cap instead so people without sufficient amount of tokens can also stake and participate in the consensus process.

11

Good question. So my understanding is that Algorand uses VRF to select a subset of validators as the candidates for the next block proposer. However, since multiple validators might be selected by the VRF, Algorand needs to run a Byzantine Agreement protocol to determine the block proposer (only one validator can be elected). Instead, the VDF puzzle (seeded by VRF) in our proposal creates runtime randomness to “select” the next block proposer in a way similar to Bitcoin PoW.

12

One challenge though, is that different implementations could have vastly different speed solving the same VDF. For example, an ASIC solver could be 20 times faster than a software solver running on CPUs.

To address this at the protocol level, one idea is to increase the puzzle difficulty for the current block’s proposer for the next N blocks. This reduces the chance this validator is selected again as the block proposer in the near future, effectively reducing his speed advantage.

For example, suppose we have N validators, and a few of them is m times faster than others in solving VDF (in practice there is like a bound on m , e.g. m < 20). We can impose a rule that for the current block proposer, the puzzle difficulty is increased by 2^m times for the next N/2 blocks on the same chain:

K(H(r)^{2^T}) < M/2^m

This kind of rules can be enforced since in PoS chains, typically a validator needs to lock its stake for a long time. As the difficulty is increased tremendously, with high probability, any node can be elected as the proposer at most twice within N consecutive blocks. On the other hand, the expected number of times a slow node can be elected as the proposer is roughly 1. Hence this could reduce the advantage of the faster node from m down to 2.

13

But this method of temporarily increasing the difficulty for specific block proposer gives rise to sybil attacks, right?
Now validators prefer splitting their stake to many different accounts, so if one of their accounts gets to be the next proposer only this account is “penalized” with the difficulty increase.

14

Good point, the adversary can also attack by withholding their blocks and wait for the honest nodes to get “penalized”. We have some new thoughts on how to address the speed difference without penalizing the block proposers. Will post it shortly.

15

In this post, we will present a protocol modification that can hopefully eliminate the solver speed advantages. For simplicity, below we only discuss the case where all the validators have the same amount of stake and require at least 2/3 of all nodes are honest. The more general cases can be analyzed similarly.

Recall that in the design discussed in the original post, as soon as an honest validator node sees a valid block for the same height it is working on, it simply gives up and switches to mine on top of this new block. Such a rule bias towards validators with fast VDF Puzzle solvers. To put all the validators back on the same playground, we notice that the T value (i.e. the number of sequential steps required to solve the VDF Puzzle) in the solution of the VDF puzzle is independent of the solver speed. If the protocol elects the block proposer based on the T value instead of the puzzle solving time, the probability that a node is elected as the block proposer can be decoupled from the VDF puzzle solver speed.

With this insight, we propose the following modification. A validator v should solve its assigned puzzle by trying T = 1, 2, 3, .... While it iterates through these values, another validator u might have already solved its puzzle for the same block height and proposed block B_u. The header of B_u contains the puzzle solution T_u. When validator v receives this block, it compares T_u with the t value it is currently evaluating. If T_u < T, then clearly the solution of the puzzle assigned to validator v is larger than T_u. Validator v should just discontinue his effort solving the puzzle and instead accept block B_u. Otherwise, it continues to solve its puzzle until the solution is found or a timeout reached. In the special case where all the validators have the same VDF puzzle solver, this modified protocol is equivalent to the design discussed in the original post.

We note that with this change, the longest chain rule no longer applies. This is because a validator with a fast VDF puzzle solver can still have advantage in generating longer chains. Instead, we resolve the forks by the chain quality. First let us define the block quality, which can be used as the building block for defining the chain quality. Intuitively, given two blocks, the one with a smaller T value in the puzzle solution should have a higher quality score. Thus, we can define the block quality for a block at height i as:

QB_i = E_{1/2}[T_i] - T_i

Here E_{1/2}[T_i] is the expected minimum number of steps that one of the validator solves its puzzle at height i, assuming half of all validators compete to solve the puzzles. T_i is the actual puzzle solution T stored in the block header. This expectation can be easily derived from the number of registered validators at height i and the threshold M in the puzzle definition. A block with a higher block quality is more preferable.

The intuition behind this definition is that if less than 1/3 of the nodes are malicious, even if all of them collude, on average the expected minimal T value generated by the malicious nodes should be smaller than E_{1/2}[T_i] with high probability. Thus, the blocks generated by them are likely to have negative quality scores. Hence, it is useless to generate a long chain with fast VDF puzzle solvers. Also, note that with this definition, to guarantee liveness, we also need to assume that at least half of the registered validators are both active and honest at any time.

The chain quality can thus be simply defined as the sum of the block quality:

QC = \sum^{n}_{i=1}{QB_i} = \sum^{n}_{i=1}{(E_{1/2}[T_i] - T_i)}

Here n is the total number of blocks on the chain. A chain with a higher QC will be favored by the honest nodes.

We will omit the formal analysis of this protocol modification here. However, as mentioned above, it is worth pointing out that an adversary with a very fast VDF puzzle solver might be able to generate a longer fork than the main chain. However, with overwhelming probability, this longer fork will have lower chain quality than the main chain if the adversary controls less than 1/3 of all nodes. This is because in his fork, highly likely the block quality is negative for most of the blocks. Thus, an adversary should have negligible chance to revert the main chain by performing either the “nothing-at-stake” or “long range” attack.

16

Hi guys, any comments on my VDF&VRF based PoS?

  • Winner-takes-all is avoid by exponential VDF steps that adjust using average block time.
  • VRF (ie. bijective signing) and current stake is used to generate pseudo-random seeds for each miner to calculate their current block VDF steps to compute. Basically is a Synthetic Proof-of-Work, because we are simulating Random Clocks.

Thanks!

Draft:

Very basic Proof of Concept (with pseudo-VDF):

Consensus:

vixify-README-md at master · manfr3d-vixify 13-04-2020 17-38-38
vixify-README-md at master · manfr3d-vixify 13-04-2020 17-38-381894×1582 545 KB

Winner-takes-all Protection draft:

difficulty = slow-moving variable self-regulated by average block time (for example, miners can move this deterministically by 1% each block up or down).

minerStake = current block # of coins stake of the miner address holding the coins

stake = minerStake / totalCoins 

slot = int(round(1/stake))

miner_vrf_seed = vrf_sign( prev_block_hash, miner_private_key ).    # VRF is just a deterministic signature, bijective.

random.set_seed(miner_vrf_seed)

slotRange = [1:slot+1] # the range of possible integer slots for a given miner holding stake on a given address.

slotNumber = random.random_integer_on_range(slotRange) # slotNumber = a deterministic slot number based for address or miner holding stake on a given blocknumber.

vdfSteps = 2 ^ ( difficulty * slotNumber )   # this number is like the average mining time of traditional PoW.