Negative Price AMM

[v-for-vasya]

TL;DR: We discover that negative liquidity is possible and construct an AMM to access the negative domain by allowing the price to go negative. The invariant for a negative price happens to be the formula for a circle and the liquidity distribution happens to have a power law tail. You can interact with and compare it to an RMM here. Most interesting points are outlined below with link to paper at the end.

Figure 1:Two negatively priced assets can be exchanged between each other for a positive price. An impossible task in tradfi, requiring a fiat numeraire to act as an intermediary.

---

Summary:
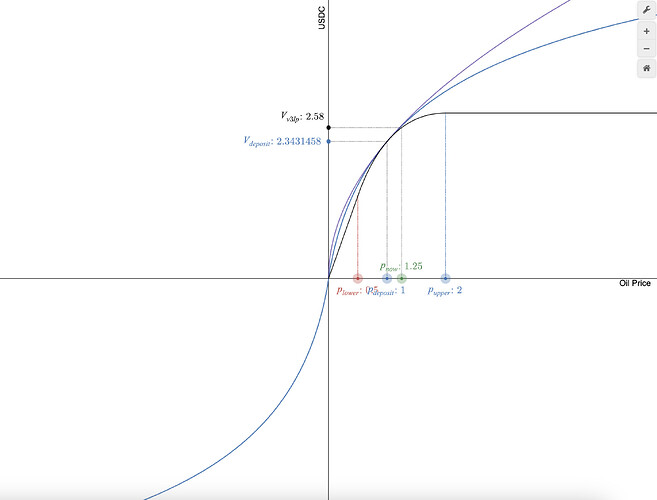
Swapping and liquidity provision transactions of a Concentrated Circular Market Maker (CCMM) are obfuscated using Fully Homomorphic Encryption (FHE) to mitigate MEV in the public mempool by combining game theory with the Kelly criterion. Liquidity of the CCMM is adjusted using a scale parameter and can be modified with a hook in Uniswap v4. We show how it is possible to enter the negative liquidity domain with the CCMM.

---

Negative Liquidity

If we look at a Constant Product Market Maker (CPMM) such as Uniswap, we can see that it happens to provide liquidity in the negative domain. Take the Uniswap Invariant with liquidity L

xy=L^2

introducing price p as p = y/x and y = px

xpx=L^2

solving for x

x=\sqrt{\frac{L^2}{p}}

note the appearance of a negative sign

x=±\frac{L}{\sqrt{p}}.

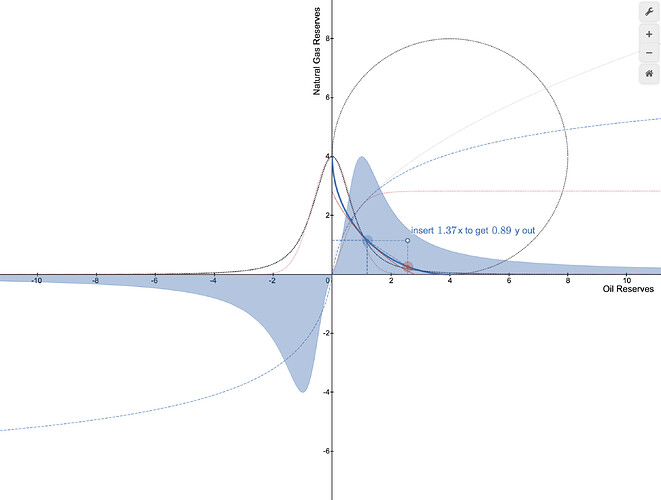
It’s just difficult to access this negative liquidity in Uniswap due to the invariant being a hyperbola. By pressing the invariant against the axes, concentrating liquidity, and folding it on itself we can travel to the negative domain. A liquidity provider may become a liquidity taker with the following invariant where z is a scale parameter

(x−z)^2 +(y−z)^2 =z^2.

We like to call it the DiracAMM (Paul Dirac discovered anti-matter with a similar trick by seeing that energy \sqrt{E^2} could have a negative value in the energy-momentum relation). One can program the invariant to not provide liquidity after touching the axes though, in which case its liquidity distribution L happens to be the Student’s-t distribution with degree of freedom df=2, a special case of a power law tail where the law of large numbers has no predictive capacity on the variance.

L_{Student-t}(x) = \frac{1}{(1+x^2)^\frac{2}{3}}

LP Payoffs

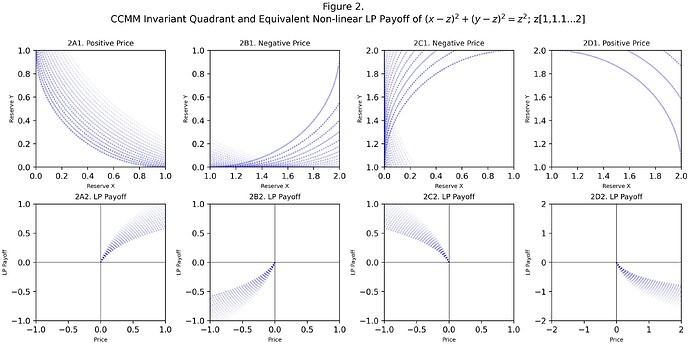
If price, following a power law, is allowed to flow into the negative, as is empirically observed with various assets, then the LP payoff function happens to resemble a collection of non-linear payoffs.

But it’s not necessary though for the underlying price to be negative for this AMM to be useful. Rather, one suggestion is to use the price of $0 as an offset from the current underlying price of, let’s say $100 . A negative 1 price indicates a decline of the underlying from $100 to $99. If the CCMM has one asset that can not go negative, such as a stablecoin, then it can only have LP payoffs 2A2 and 2B2, but by borrowing the LP position through a lending protocol one could mimic the payoffs of 2D2 and 2C2 respectively.

MEV approach with Kelly Criterion and FHE

Since a gain and a loss can be defined as an offset with a CCMM, we can combine it with the game theory behind rational MEV decision makers who follow the Kelly criterion, a strategy that ensures long-term optimal geometric growth

f∗= p - \frac{1-p}{b}

where f∗ represents a MEV extractor’s portfolio allocation in a MEV attack with the probability of success p and betting odds b. By targeting Kelly-neutrality we set a MEV extractor’s Kelly betting amount f = 0 at an increased gas cost by rearranging for the following equality to hold

p=\frac{1-p}{b}.

We do so by introducing two encrypted boolean values (ebool) for swapping B_{swap}=[0,1] and providing liquidity B_{LP}=[0,1] going into the mempool. Where the boolean value can mean 1 for swap x for y and 0 for swap y for x (or remove and re-add liquidity for B_{LP}). We can also encrypt the swap quantity dx (or dy) as euints, thereby making it unclear what the betting odds b (gain and loss relationship) are.

E⟨B_{swap/LP}⟩=\frac{1-E⟨B_{swap/LP}⟩}{\frac{E⟨Gain⟩}{E⟨Loss⟩}} = \frac{1-0.5}{\frac{x}{x}}=0.5

Setting the expected value of a MEV extractor’s Kelly bet E⟨f∗⟩ = 0. Targeting Kelly-neutrality could be a useful mechanism for MEV. We noticed that with FHE we can selectively target just the variables we want to obfuscate enough without having to encrypt everything and think that this approach could be useful to others looking into MEV.

Further work

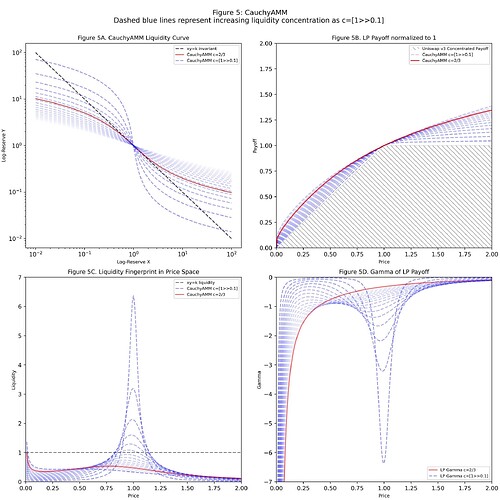
An approach to avoid negative prices for the underlying could be to construct a passive wall of liquidity, a liquidity fingerprint that asymmetrically increases non-linearly as price approaches zero, denting price impact. The super-heavy tailed distributions like the Log-Cauchy distribution with concentration parameter c come to mind with liquidity fingerprint in price space being

L_{Log−Cauchy}(p) = \frac{1}{\pi p} \frac{c}{ln(p)^2+c^2}.

This is a very interesting liquidity fingerprint because it captures what we see in crypto where some tokens stay where they are, the majority approach the zero bound, and a select few fly towards the right tail. One of the mathematical challenges here being that liquidity spikes to infinity at 0 though.

Our paper with more interesting details is on GitHub

[Pfed-prog]

Here is an excerpt from the paper

I am very curious how negative liquidity would affect the LPs pay outs in contrast to Uniswap V2 and V3.

[v-for-vasya]

Just added a desmos example here that shows how a CPMM (uni v2), CLMM (uni v3), and CCMM would differ from each other. For the sake of simplicity, I used oil priced in dollars (which has gone negative before) and set the price to 1 and matched the amount of liquidity in each LP payoff for ease of comparison.

In the case of an LP position consisting of both assets going negative (let’s say a token pair of oil/onions), the payoff would go to infinity on one end and emerge on another, creating an infinity loop:

I used onions as an example because they also went negative before. In 1958 Congress had to pass the Onion Futures Act banning the trading of onions as the price went negative at the CME. This applies only to the US, but DeFi is permissionless. The ability to trade two negatively priced assets appears to be a unique feature in DeFi that is just not possible in TradFi where one has to go through a numeraire such as the US Dollar to trade a negatively priced oil barrel for a negatively priced natural gas BTU instead of exchanging them directly through a token pair.

Additionally, a potential application of negative prices besides commodities that can go negative (oil [1], natural gas [2], onions [3], electricity [4]) could actually be some form of a reputation token.

For example, reputable individuals in an industry, or famous personalities, or reputable DAOs, or brands may issue a token that can be redeemed for time spent with such an entity or services rendered.

If a reputation token does go beyond the zero bound after a large sale, maybe an insider was simply interested in making a quick buck or a scammer was aiming to simply deceive uninformed people. By having a zero bound, the insider and scammer would be able to extract value due to information asymmetry versus the uninformed token purchasers since the price can only crash to zero.

If a reputation token LP pair creator does not allow for the entry into the negative domain, then it would look incredibly suspicious in a world where reputations can go negative!

This might help deal with a lot of the anonymous scams one sees in crypto where v2 LP pair names with a zero bound are created. If a company/person/token/DAO truly is legit, then one shouldn’t worry if one’s token price can go negative. A kind of skin in the game.