NFT Price Oracle: A credibly neutral algorithm for NFT price discovery

Applications
1

by @black71113 @yusenzhan

Unlike fungible tokens, NFTs lack real-time pricing due to their non-fungibility and illiquidity. Prices are typically referenced to the floor price, which lacks item-level granularity. This makes it difficult to price non-floor-valued NFTs for trading or lending.

Specifically, in these applications:

  • As a reference price for peer-to-peer transactions
  • Calculating personal or institutional NFT portfolio valuations
  • NFT lending, fractionalization, and other NFTfi applications

There is a lack of a credibly neutral and fair price at the item level.

Many applications try to provide pricing services via ML models, but the complexity and lack of transparency make it hard to gain trust and consensus.

This article attempts to provide real-time NFT pricing with a simple and interpretable algorithm. It also proposes an oracle mechanism for stakeholders to participate fairly in price discovery. It follows principles of credible neutrality with minimal objective data and simple, understandable, and robust models for easy adoption.

Premium Model

Through observations of large amounts of blue-chip NFT transaction data, we find that the value of traits is roughly constant relative to the floor price. When the floor price rises and falls, the absolute premium of each trait will fluctuate accordingly, but the ratio to floor price remains stable. This means the relative premium relationships between traits are stable. We refer to premium of a NFT trait over floor price as the trait premium. We therefore hypothesize:

  • The value of a NFT can be decomposed into the inherent value of the collection itself and the sum of all trait premiums.
  • The ratio of trait premium to floor price is largely constant within a period of time.

Thus, we propose the Premium Model. The core formula underpinning the Premium Model is expressed as:

\begin{equation}\begin{aligned} \text{Estimated price} & = \text{Floor price} \times (1 + \text{Intercept} + \sum \text{Trait weight}) \\ & = \text{Floor price} \times (1 + \text{Intercept}) + \sum \text{Floor price} \times \text{Trait weight} \\ & = \text{Base value} + \sum \text{Trait premium} \end{aligned}\end{equation}

Here:

  • Estimated price: The predicted value of the NFT.
  • Floor price: The lowest price at which an NFT is currently listed for sale in a particular collection on the market.
  • Intercept: This could be considered as a base adjustment to the floor price. Since the base value of an NFT excluding traits should be between floor price and best offer, the intercept is usually a tiny negative amount.
  • Base value: This represents the baseline value of an NFT within a collection not tied to specific traits, derived from the floor price and influenced by an intercept. Mathematically, it can be represented as:
\text{Base value} = \text{Floor Price} \times (1 + \text{Intercept})
  • Trait weight: These are the coefficients that are assigned to each trait to determine how much that trait influences the price of an NFT. Each trait contributes proportionally to the estimated price based on how it is valued relative to the floor price.
  • Trait premium: Additional values attributed to particular traits of the NFT. They are the product of floor price and their corresponding trait weights.

After a simple transformation, (1) yields

\begin{aligned} \begin{aligned} \frac{\text{Estimated Price}}{\text{Floor Price}} -1 = \text{Intercept} + \sum \text{Trait Weights} \end{aligned} \end{aligned}

Rename \frac{\text{Estimated Price}}{\text{Floor Price}} -1 to \hat{y}, and rewrite \text{intercept} + \sum \text{Trait Weights} to linear regression form, then we get

\hat{y} = \mathbf{w}^T \mathbf{x} + b

Where \mathbf{w}^T \mathbf{x} is computed as the dot product of the two vectors, which is:

\begin{aligned} \mathbf{w}^T \mathbf{x} = w_1 \cdot x_1 + w_2 \cdot x_2 + \ldots + w_n \cdot x_n \end{aligned}

In a practical use-case, suppose you have 3 traits (A, B, C）. An NFT with traits B and C would be represented by the one-hot vector \mathbf{x}=[0,1,1]. The linear regression model predicts the NFT’s price based on the learned weights for each trait and the intercept so that we can rewrite \sum \text{Trait Weights} as \mathbf{w}^T\mathbf{x} .

Evaluation

We used:

  • all real on-chain transaction data within two years as training data
  • whether the transaction data was in a loop as the criterion for identifying wash tradings
  • lowest listing price of opensea, blur, and looksrare as the floor price
  • Lasso Regression as the regression model

to train a separate model for each collection.

Whenever a transaction occurs, we record the on-chain sale price, as well as the model’s predicted price at that moment. We compiled the latest 100 transactions, and calculated the average accuracy. We tested the model on blue-chip collections and employed Mean Absolute Percentage Error (MAPE) as evaluation metric. Here is the test result.

Collection MAPE
Bored Ape Yacht Club 96.366%
Azuki 92.186%
Doodles 95.885%
Degods 99.022%
Mutant Ape Yacht Club 97.184%
Otherdeed for Otherside 83.407%
Cool Cats NFT 92.174%
CLONE X - X TAKASHI MURAKAMI 95.510%
Moonbirds 90.040%
CryptoPunks 87.860%

The fact that time range selected for training data spans two years and a high accuracy rate is obtained on the lastest 100 transactions, indicates the assumption that the average premium ratio between different traits represents the value well holds true for most blue chip collections.

The following list is the trait weights for trait Fur of the collection BAYC.

Trait value of Type Fur Trait weight
Solid Gold 9.30424
Trippy 3.34777
Death Bot 0.22485
Noise 0.14102
Robot 0.13671
Cheetah 0.07087
Dmt 0.05786
Blue 0.03495
Zombie 0.03469
White 0.02176
Brown 0.00905
Pink 0.00534
Black 0.00156
Cream 0
Dark Brown 0
Golden Brown 0
Gray 0
Red 0
Tan 0

It can be seen that the trait weights of the most valuable, Solid Gold Fur and Trippy Fur, are 9.3 times and 3.3 times the floor price, respectively, which are significantly higher than all other weights, while many ordinary traits have a weight of 0. These results are very consistent with our understanding of trait value.

Due to the low liquidity of rare NFTs and insufficient data collected, it is currently impossible to provide accurate accuracy data for rare NFTs. However, we can give a specific example to illustrate.

1370Ă—1082 115 KB

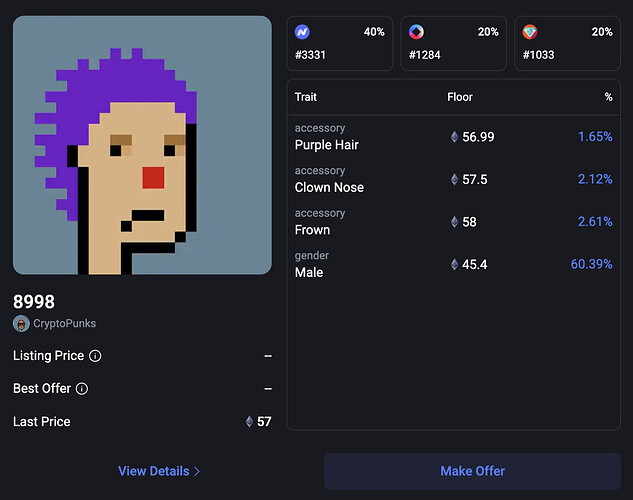
On October 15 2023, a transaction of Cryptopunks #8998 occurred. The transaction price was 57 ETH, and the floor price at that time was 44.95 ETH. We recorded the trait weights of #8998 at that time as follows:

  • Accessory Purple Hair: 0.15931
  • Accessory Clown Nose: 0.02458
  • Accessory Frown: 0
  • Gender Male: 0.05595

The intercept of Cryptopunks was -0.03270.

So the valuation can be calculated from:

\begin{aligned} \text{Estimated Price} & = \text{Base value} + \sum \text{Trait Premiums} \\ & = \text{Floor Price} \times (1 + \text{intercept}) + \sum \text{Floor Price} \times \text{Trait Weights} \\ & = 54.26 \text{ETH} \end{aligned}

It is close to the transaction price, with an error within 5%.

However, not all rare NFTs can be priced so accurately. Due to unclear value, people often overestimate or underestimate when giving prices for rare NFTs, which introduces bias that objectively exists. Therefore, no matter how the NFT pricing algorithm is designed, there is always an upper limit on accuracy.

However, from the above data, we can see that the trait premiums calculated by this algorithm are significant in two aspects:

  • The value of rare traits is distinctly differentiated from ordinary ones.
  • The process of differentiating these premiums is transparent, evidence-based, and credibly neutral.

NFT Price Oracle

Although the algorithm aims to be as credibly neutral as possible, some issues remain:

  • Off-chain prices can not be used for on-chain transactions.
  • Single centralized node poses manipulation risks.
  • It is difficult to reach consensus on the algorithm of identifying wash trading for training data and requires a consensus confirmation mechanism.

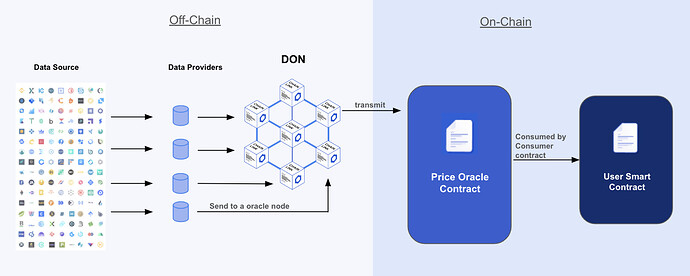
To provide a credibly neutral on-chain price resistant to centralized manipulation, we design an oracle mechanism to achieve consensus.

1628Ă—652 119 KB

It consists of a decentralized network of nodes:

  • Participant Nodes: Each node obtains training data from on-chain transactions, calculates trait weights using the open-source algorithm, and submits them to oracle nodes, forming Decentralized Oracle Networks. Each node can choose different:
    • Linear models—such as naive linear regression, lasso regression, ridge regression, etc. Lasso regression is recommended as it can reduce unimportant trait weights to zero.
    • Algorithms for identifying wash trading.
    • Transaction histories within a suitable timeframe. The greater the change in the trait weights of the collection, the smaller the timeframe for the transaction history should be. But a smaller timeframe is more detrimental to accuracy, so it is a trade-off. For the general case, using all historical transactions is recommended.
  • Price Oracle Contract: It operates in two steps:
    • Validate all returned trait weights, taking the median or average after removing outliers. As trait values are relatively stable, weights should not differ much, keeping deviation low after validation.
    • When a user calls the price oracle contract, it first obtains the real-time floor price through the floor price oracle and then calculates real-time pricing using formula (1).
  • User Contract: Pass the contract address and token ID to retrieve specific token pricing from the price oracle contract

As trait value ratios remain stable over time, it is unnecessary for trait weights to update frequently. Periodic weight updates from oracle nodes, combined with real-time floor pricing, maintain accurate real-time item-level NFT pricing.

However, if we choose not to use this model with weights, and instead only reach consensus on the final generated price, would it still work? Different pricing models can have a significant impact on the pricing results. The same rare NFT could be estimated at 120 ETH or 450 ETH. Taking the average or median in the presence of such a large bias would still introduce tremendous errors. However, the introduction of weights can largely ensure that the price fluctuation range remains small and provide logical explanations for the pricing origin.

Strengths

Credible neutrality

We strongly believe that this pricing process should be as credibly neutral as possible; otherwise, it cannot become a consensus for all NFT traders. Throughout the entire design process, we have tried to adhere to the four basic principles of credible neutrality:

  • Don’t write specific people or specific outcomes into the mechanism: Avoiding third-party biases such as rarity or sentimental value, the parameters/weights are deduced through a linear regression. This is strictly grounded in transaction history and utilizes only sale prices and floor prices as inputs during training.
  • Open source and publicly verifiable execution: The linear models are completely open source, and off-chain model training and on-chain price generation are both easily verifiable.
  • Keep it simple: The Premium Model employs the simplest linear model and uses as little training data as possible. The price calculation is a simple summation. The NFT price is linear to the floor price.
  • Don’t change it too often: Trait weights do not require frequent changes, making it less likely to be attacked.

Transparency

The introduction of trait weights is important. Most machine learning models are black boxes, lacking strong transparency, making it difficult to trust the resulting prices and impossible to reach a consensus. However, the introduction of trait weights makes prices easy to understand, giving each parameter a clear meaning: trait weights represent the ratio of trait premium to floor price, and intercept corrects the floor price and provides a base value for the collection. Trait weights are shared among each NFT price, just like traits are shared among each NFT.

Limitations

Despite its strengths, some limitations exist:

  • It is not applicable for rapidly changing trait values. Because the prior assumption that the premium of a trait is roughly a constant parameter relative to the floor price, when the value of the trait changes rapidly, the range of trait value fluctuations calculated based on trading history of different time lengths is very large, which reduces model accuracy. Even if consensus can be reached neutrally through an oracle, it is still a compromise solution.
  • It is vulnerable to wash trading attacks. The Premium Model relies on real transaction data. Wash trading distorts pricing inputs, leading to distorted pricing outputs. While decentralized oracle networks provide wash trade filtering, this adds uncertainty.
  • It is not fully permissionless. Oracle nodes currently require vetting to prevent Sybil attacks.

Applications

The NFT price oracle has numerous applications, particularly in NFT lending, leasing, Automated Market Makers (AMMs), fractionalization, and other NFTfi applications. It can also serve as a reliable reference for peer-to-peer transactions.

The feature of linearity enables proportional fragmentation. Currently, NFT AMMs or fractionalization protocols use multiple pools for different NFT values, leading to fragmented liquidity. With stable price ratios, a new fragmentation approach can consolidate an entire collection into a single vault. In this setup, the collection’s ERC20 uniquely represents the entire collection.

For example, in the case of Bored Ape Yacht Club (BAYC):

  • Rare NFT #7403, worth 104.4 ETH, can be collateralized into 1044 xBAYC.
  • Common NFT #1001, worth 25.5 ETH, can be collateralized into 255 xBAYC.

When the BAYC floor price drops from 25 ETH to 12.5 ETH, 1 xBAYC drops in value from 0.1 ETH to 0.05 ETH. But their value ratio remains unchanged at 1044:255.

Price ratios remain constant despite changes in the floor price, allowing for fair fragmentation and redemption.

Acknowledgements

This work is greatly inspired by two articles written by @vbuterin . The article Credible Neutrality As A Guiding Principle provides us with direction in establishing credibly neutral mechanisms. The article What do I think about Community Notes shows a concrete example on designing an algorithm following principles of credible neutrality.

But NFT pricing is different from Community Notes in that, since the price data in trading scenarios must be real-time and have zero risk of manipulation, open-sourcing the code alone is insufficient for true credible neutrality. An effective on-chain consensus mechanism must be established.

5 Likes