Authors: pop
This post is based on the current spec of PeerDAS
Edited after @leobago’s comment
This post will tell you the expected number of peers each node must connect to in order to cover all the columns to do peer sampling successfully.
Simulation
In PeerDAS, at the time of writing, the number of peers you are expected to connect to is solely calculated by CUSTODY_REQUIREMENT and DATA_COLUMN_SIDECAR_SUBNET_COUNT. We write the following simulation to count how many peers you need to connect.
import math
import random
def peer_count(N, C):
num_trials = 1000
counts = []
for trial in range(num_trials):
covered = set()
count = 0
while len(covered) != N:
selected = set(random.sample(range(N), C))
if len(selected.difference(covered)) > 0:
covered = covered.union(selected)
count += 1
counts.append(count)
return sum(counts)/len(counts)
where N and C are DATA_COLUMN_SIDECAR_SUBNET_COUNT and CUSTODY_REQUIREMENT, respectively.
What this function does is to simulate the node discovery mechanism. What it does in the real world is that the node will discover new peers and find out what subnets the peer is taking custody of. It will continue discovering new peers until all the subnets are covered by those peers. What’s important is that the node will not keep a peer that doesn’t add any more coverage to the subnets. So when N=32 and C=1, peer_count will be exactly 32.
The set of subnets each peer is supposed to custody is determined by its Peer ID. However, in our simulation, such set is just randomized, which shouldn’t be different from the real world.
In order to get the expected number, we run 1,000 simulations and get only the mean.
Result
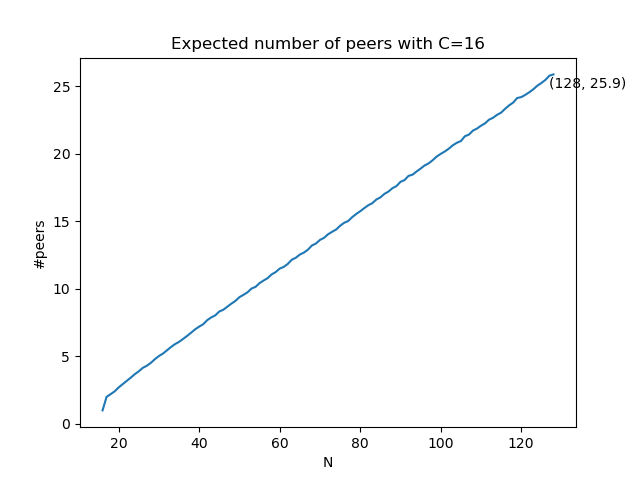
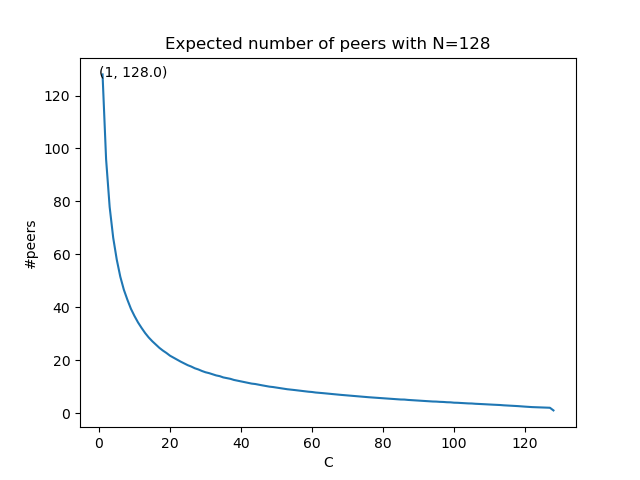
Trivially, if we fix C and make only N variable, peer_count will increase as N increases since, when there are more subnets to cover, the more peers you should have. And, if we fix N and make only C variable, peer_count will decrease as C increases since, when each peer custodies more, the number of peers you should have should be lower. Even if it’s trivial, we did the simulation for completeness.
You can see that with N=128 and C=16, you need 25.9 peers on average (so it’s far different from N/C=8).
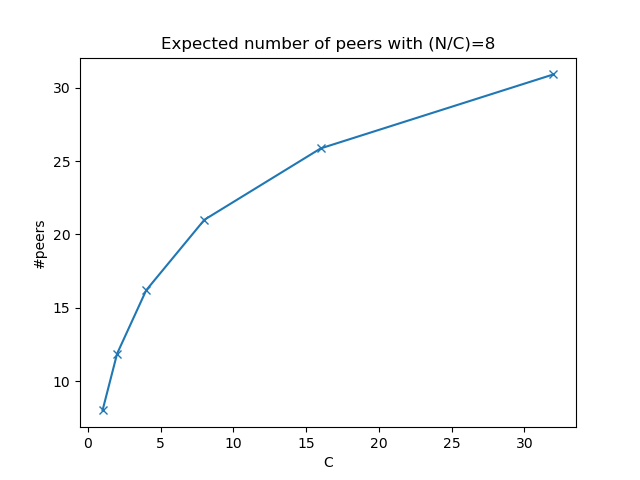
Now, let’s consider an interesting non-trivial scenario, if the ratio (N/C) remains unchanged, do you think peer_count will remain unchanged? That is, do you think peer_count(64, 8) and peer_count(128, 16) will be the same? The answer is no. As shown below, the higher N is, the higher peer_count is.
So the expected number of peers you will have cannot be easily calculated with N and C. You need to do the simulation to tune the parameters.