Onchain computation proofs for EVM

[alexeuler]

Ethereum provides two main data/call types for external RPC users: current data from regular nodes and historical data from archival nodes. However, within a smart contract or the Ethereum Virtual Machine, access is restricted to only current data.

This post presents an algorithm that allows for the validation of historical call results for any smart contract on the Ethereum Virtual Machine. The algorithm enables smart contracts to retrospectively evaluate past execution outcomes, facilitating actions such as penalizing previous actions or inactions and reacting to events that happened but weren’t logged on the blockchain.

Contents

• 1 Introduction

• 2 Zero knowledge proofs for storage slots values

• 2.1 Components of the Proof System

• 2.2 Proof of Blockhash

• 2.3 Proof of Storage

• 2.4 Effectiveness for Proof of computation

• 3 Onchain Computation Proofs

• 3.1 Onchain EVM

• 4 zkEVM Computation Proofs

• 5 Use cases

• 5.1 Decentralized Onchain Dutch Auctions

• 5.2 Keeper Network

• 6 Conclusion

1 Introduction

The growth of Ethereum’s smart contract ecosystem has been impressive, driven by the idea of smart contracts working together. This allowed them to share data and make updates easily. This feature, called composability, helped decentralized applications on Ethereum expand quickly.

But there was a limitation. Smart contracts were capable of accessing only the most recent data on the blockchain, lacking the ability to retrieve historical information. To illustrate, if a contract needed the latest price information, it could make a call like this: Oracle.getPrice("USDC", "ETH"), which would provide the current ETH/USDC price to the contract. Yet, it was impossible to specify a past block to obtain the price at that particular point in time. To fix this, Ethereum introduced the BLOCKHASH opcode, which in theory, let developers access past block data:

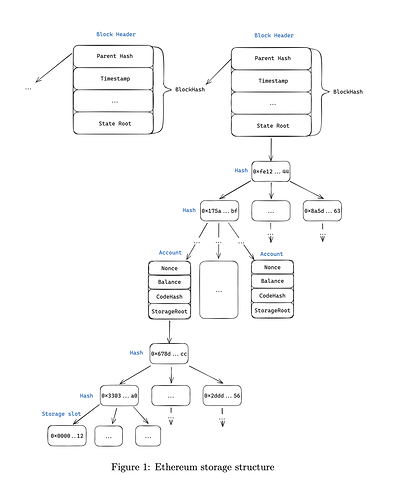
Blockhash is a cryptographic hash of the entire Ethereum state at this block (see Table 1). This means you can prove the historical value for any storage slot in block number BN in two steps:

1. Prove that the blockhash of block BN equals the value BH.

2. Using BH, prove the value V for a storage slot SS.

The proof consists of two parts:

1. The block headers from the current block going back 256 blocks, up to block BN (or it may be empty if BN is in the most recent 256 blocks).

2. The Merkle-Patricia proof of the storage slot value with the State Root of block BN and the blockhash BH.

See Figure 1 for details. The proof verifier (a smart contract) will perform the following steps:

1. Retrieve the blockhash of the block closest to block BN using the BLOCKHASH opcode.

2. If block BN is not among the recent 256 blocks, use the last available onchain blockhash (current - 256).

3. From this block header, obtain the blockhash of the previous block.

4. Repeat this process until the blockhash BH of block BN is proven.

5. Verify the Merkle proof of the storage slot SS using blockhash BH.

This is the most straightforward approach, enabling the proof of historical storage slot values. Utilizing solely this method, it is possible to implement historical oracles within smart contracts (as specified in this article). The only drawback of this approach is the gas costs. The proof of each storage slot results in approximately 400k gas consumption, which increases the further we look back into the past. While this works well on Layer 2 solutions where gas costs are low, it’s often prohibitive on the Ethereum mainnet.

Axiom and Herodotus take this approach a step further by using zero knowledge proofs (ZKP) to prove storage slots and arbitrary computations over storage slots. The core advantage of this approach is that ZKP proofs can be aggregated. With a fixed gas cost of around 300-500k, you can obtain proofs for many storage slots and even computations over these slots.

2 Zero knowledge proofs for storage slots values

The concept of aggregating storage proofs into a single zero-knowledge proof (ZKP) is fundamental in reducing gas costs for verification. This approach is extensively documented in the Axiom Documentation and the Herodotus Documentation. In this section, we provide a brief summary to ensure the completeness of our discussion. If you’re already familiar with these solution, feel free to skip to section 3.

2.1 Components of the Proof System

The proof system under consideration has several components:

1. Proof of Blockhash: This involves having an onchain Merkle proof for all block number-to-blockhash pairs

2. Proof of Storage: This part focuses on generating proofs for storage slots corresponding to a specific blockhash

2.2 Proof of Blockhash

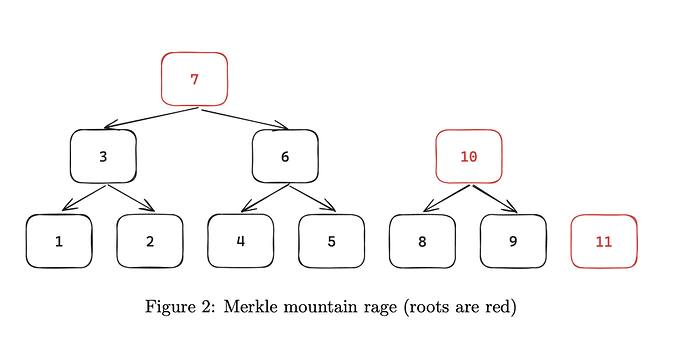
The process of storing proofs of blockhash utilizes a cryptographic structure known as the Merkle Mountain Range (MMR). MMR is a specialized data structure that combines the concepts of a Merkle tree and a mountain range. Its primary purpose is to efficiently store and verify large sets of data, particularly in append-only contexts like blockchain. Unlike traditional Merkle trees, which are binary and balanced, MMRs consist of several smaller, individual Merkle trees, often referred to as ”peaks,” arranged to form a range or sequence. (see Figure 2)

Each peak in a Merkle Mountain Range is itself a perfect Merkle tree, and these peaks vary in size. This variation allows for efficient append operations, as new data can be added without needing to restructure the entire tree. The root of an MMR is the combination of the roots of these individual peaks, and it provides a cryptographic proof of the entire dataset.

Each leaf in MMR is a blockhash of a specific block. A dedicated smart contract is deployed to verify the correctness of MMR roots using ZKPs. The verification of a blockhash can be conducted in two distinct ways:

1. Onchain Comparison: The blockhash is compared directly to the output of the BLOCKHASH opcode on the blockchain

2. Hash Chain Validation: In cases where the onchain comparison is not

feasible, the validity of the blockhash is ascertained by verifying its hashchain linkage to known blocks. This method is visualized in Figure 1, which illustrates the chain of hashes leading back to a known block.

The process of bringing the MMR roots onchain is executed in two primary stages:

1. Initial Setup Phase: This stage involves the generation of the MMR root for all blocks up to a recent block. It establishes a foundational state from which subsequent verifications can proceed.

2. MMR Root Updates: Following the initial setup, the MMR root is regularly updated to bring all blocks up to the current point in the blockchain.

This continuous update ensures that the proof system remains current and reliable.

2.3 Proof of Storage

With the accessibility of onchain proofs for blockhashes now established, the next crucial step involves generating ZKPs for a specific set of storage slots. The process is based on converting the standard Ethereum Merkle-Patricia proofs into a format compatible with ZKPs. This conversion process involves encoding the traditional proofs into a structure that can be efficiently processed and
verified through ZKP algorithms. Once the proofs are translated into the ZKP format, the final step is to submit these proofs to Ethereum. ZKPs are more gas-efficient compared to the conventional onchain verification methods with Merkle trees.

2.4 Effectiveness for Proof of computation

Axiom implements a ZKP system that uses storage slots and other blockchain data. The system is designed to prove arbitrary statements about the historical state of Ethereum. Theoretically, this ZKP system has the capacity to perform arbitrary computations. However, in practice, these computations must be implemented in specialized languages tailored for zero-knowledge applications, such as Halo2, Circom, or Cairo. This requirement presents a practical limitation, particularly when verifying the historical execution of contract calls on the blockchain.

For effective verification, one would need to translate or port the smart contracts, along with any dependent contracts, from Solidity (the native language of Ethereum smart contracts) to one of these ZKP-compatible languages. This translation process is not only technically demanding but also makes the task of verifying historical contract executions somewhat impractical.

3 Onchain Computation Proofs

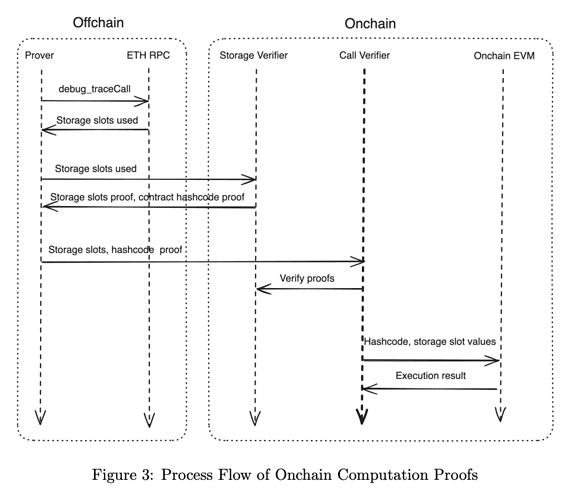
In addressing the challenge of verifying historical onchain calls, we propose a comprehensive multi-step process that integrates both offchain and onchain components, as illustrated in Figure 3.

The suggested process is broken down into a few steps:

1. Use the offchain RPC API (specifically the debug_traceCall method) to retrieve storage slots and their corresponding values for a particular onchain call at a given block.

2. Use the acquired data to interact with a storage prover, subsequently obtaining a proof.

3. Additionally, get a proof of the contract’s hashcode at the time of execution. The storage provers we mentioned earlier are capable of generating this proof as well.

4. Forward the storage data and hashcode to a verifier smart contract.

5. The verifier, in turn, confirms this data onchain through the use of Storage Verifier smart contracts.

6. The verifier then submits the storage slot values and hash code to an onchain EVM implementation (as discussed below).

7. The onchain EVM retrieves the current contract code, matches it with the provided hashcode, and executes the code. However, rather than reading actual values from the storage, it uses the supplied storage values.

8. Finally, the result of the call is returned to the verifier for final analysis.

This approach makes the computation proof viable for any smart contract execution. All that is required are storage proofs and a single onchain EVM implementation applicable to all contracts that have ever existed on the Ethereum blockchain.

3.1 Onchain EVM

An EVM is a state transition function that alters the state in response to an

Ethereum transaction. The function can be represented as:

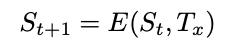
where St+1 is the state after the transaction,St is the state before the transaction, and Tx is the transaction.

The EVM has a finite set of opcodes, each altering the Ethereum state in its own specific way. It incorporates four types of memory:

• Stack

• Calldata

• Dynamic

• Storage

Thus, we can model the execution context of the onchain EVM as shown in Table 2.

Then for every EVM instruction we’ll make a state transition. For all opcodes it’ll behave exactly the same as EVM except we’ll implement a custom

SLOAD code to use our slot values from the proof rather than reading them onchain. Additionally we can disable mutating opcodes like SSTORE and CALL (i.e. have only view call semantics).

Below is the reference implementation of the ‘SLOAD‘ opcode:

This approach works effectively, allowing us to create onchain proof of any historical call result. However, a primary concern now is the gas cost on the mainnet:

• Storage Proofs:The storage proofs will burn a significant amount of gas.

• Onchain EVM Execution: Additional gas costs will arise from onchain

EVM execution. However, this increase is not too substantial since no actual storage is read; the operations are limited to memory and stack. Nevertheless, there is potential to further reduce the gas cost.

4 zkEVM Computation Proofs

The final twist in our approach involves the use of zkEVM (Zero-Knowledge

Ethereum Virtual Machine) to create a ZKP of an onchain EVM execution. In

this scenario, the onchain verifier would only need to verify a single ZKP and

thus save the gas costs.

The concept appears straightforward, yet there are only a few zkEVM implementations available in the market. Prominent zkEVM providers include:

• zkSync

• Polygon

• Scrolls

While some of these platforms are already operational, they are relatively new and still evolving.

Another critical aspect to consider is the categorization of zkEVMs into three distinct levels:

1. Consensus Compatible: Ideal for our scenario, but these types of zkEVMs are currently under development and not yet released.

2. EVM Compatible: Theoretically usable, but additional steps are necessary for full compatibility with onchain EVM.

3. Solidity Compatible: Doesn’t work for our scenario.

Lastly, it’s important to consider that generating a zkEVM proof might require significant offchain resources. This factor should be carefully factored into any planning or implementation.

5 Use cases

5.1 Decentralized Onchain Dutch Auctions

A Dutch auction, also known as a descending price auction, is a type of auction where the auctioneer begins with a high asking price which is progressively lowered until a participant accepts the price.

Examples of Dutch auctions implemented onchain include:

• VRGDA (Variable Rate Gradual Dutch Auction)
• DLM (Declarative Liquidity Manager)

To commence a Dutch auction onchain, an initial call must be made, marking

the start of the auction. However, this approach presents certain challenges:

1. Centralization Issue: It requires a kind of trusted Auction Manager to initiate the auction, potentially compromising decentralization.

2. Maintenance Cost: There are ongoing costs associated with managing and executing the necessary actions.

By leveraging onchain call proofs, the responsibility of initiating the auction can be transferred to the participants (auction bidders). Here’s how it works:

• As an auction participant submits their bid, they simultaneously provide a proof that the auction should have started at a specific block in the past (a result of a previous onchain call).

• This process validates the bid and effectively initiates the auction at the same time.

This model effectively eliminates the need for an Auction Manager, leading to a more decentralized and autonomous auction process, aligning with the principles of blockchain and decentralized systems.

5.2 Keeper Network

A keeper network is a system where specialized nodes, known as keepers, are responsible for performing certain network functions. These functions can include executing transactions, managing smart contracts, or performing maintenance tasks. The key feature of a keeper network is its ability to automate these processes, which are crucial for the efficiency and reliability of blockchain operations.

One significant issue within keeper networks is the lack of a hard guarantee that a keeper will not miss a task execution. This uncertainty can compromise the reliability of the network. To mitigate this risk, some systems implement staking mechanisms for keepers, where they must stake a certain amount of cryptocurrency as a form of collateral.

However, introducing staking necessitates a mechanism to penalize (or slash) keepers for any misbehavior or failure to execute tasks. This is where the challenge lies: designing a system that can fairly and accurately identify and penalize such failures.

A potential solution to this challenge is Eigenlayer. Eigenlayer is a protocol that allows for the creation of decentralized, trust-minimized networks over existing blockchains. It works by enabling users to stake their tokens on specific network functions or validators, effectively creating a layer of accountability and security.

To leverage Eigenlayer in a keeper network, the following approach can be adopted:

• Onchain proof is submitted to demonstrate that in block X, a call was supposed to be executed by keeper Y but was not.

• Upon verification of this failure, Eigenlayer’s staking and slashing mechanisms can be used to penalize the keeper, ensuring accountability and reliability.

6 Conclusion

This article has explored the domain of onchain computation proofs, particularly focusing on the ability to create and verify proofs of historical smart contract calls within the Ethereum ecosystem.

The approach outlined here leverages the power of onchain data and zero-knowledge proofs to retrospectively validate smart contract executions. This method makes decentralized apps more transparent and trustworthy, and also creates new ways for smart contracts to interact with and check past states.