Open, Application-Driven FHE for Ethereum
I would like to warmly thank Andy Guzman, Christian Knabenhans, Eugene Joo, Gurgen Arakelov, Keewoo Lee, Nam Ngo, Rand Hindi, Sam Richards, Thore Hildebrandt, Younes Talibi Alaoui, and Yuriy Polyakov for their generous feedback.
TL;DR
-
Why this matters (and why it’s hard): Fully Homomorphic Encryption (FHE) enables computation on encrypted data, unlocking confidentiality for Ethereum smart contracts, rollups, and AI applications. However, its adoption is slowed by performance constraints, the difficulty of decentralized key management, and the ongoing search for applications where privacy benefits justify the extra cost. Overcoming these requires both technical innovation and sustainable economic models.
-
What’s here:
- Use cases (DeFi, governance, rollups, AI) illustrate how different workloads point to the need for scheme agnosticism — e.g., TFHE for Boolean logic, BFV/BGV for exact arithmetic, CKKS for ML inference, and discrete CKKS for high-throughput confidential DeFi and accounting. They also highlight the search for applications where confidentiality is critical enough to justify FHE’s current cost.
- Ecosystem map of players (Zama, Fhenix, Inco, Enclave, Phantom Zone, Sunscreen, Shutter Network, Flashbots, OpenZeppelin, Circle Research, Fair Math, OpenFHE) highlights the diversity of approaches, the technical gaps that remain, and the opportunities for interoperability.
- Potential Paths Forward outline areas for further work, such as open benchmarks, sustainable economic models, verifiable FHE (vFHE), and decentralized key management.
- Core Considerations distill recurring themes that should guide development: application-driven scheme choice, the need for verifiability, secure models for key management, and the need for security definitions that reflect real-world adversaries. In line with scheme agnosticism, the discussion highlights how different FHE schemes map to specific Ethereum use cases, showing that no single approach suffices across workloads.
Table of Contents
- Motivation
- Players
- Role of FHE in the Ethereum Ecosystem
- FHE, Blockchain, and AI
- Use Cases for FHE in Blockchain
- Use Cases for FHE and Blockchain in AI
- FHE Players in the Ethereum World
- ZK vs FHE
- Potential Paths Forward
- Core Considerations
- Conclusion
Motivation
Ethereum has powerful tools for verifiability (zkSNARKs, rollups), but confidentiality remains a missing pillar. FHE promises a way to compute directly on encrypted state without ever decrypting it — enabling confidential DeFi, private governance, and verifiable AI while keeping Ethereum’s trust model intact.
Players
A glanceable map before the deep dives below — the full list of projects and details is given further down in this document.
| Project | What they do | Ethereum connection |
|---|---|---|
| Zama | FHEVM, TFHE-rs library, confidential EVM execution | Powers L2 efforts; founding member of Confidential ERC-20 Framework |
| Fhenix | Confidential Ethereum smart contracts via FHE coprocessors | CoFHE off-chain coprocessor; SDK for encrypted computation |
| Inco | Modular confidentiality layer using FHE/MPC/TEEs | Bridges to Ethereum; founding member of Confidential ERC-20 Framework |
| Enclave | Confidential FHE coprocessor layer | Ethereum dApps call encrypted compute; results verified on-chain |
| Phantom Zone | Encrypted VM research (RISC-V + Poulpy) | Potential runtime foundation for future confidential EVMs |
| Sunscreen | FHE compiler / SDK (“one program, any chain”) | Chain-agnostic; integrates with Ethereum dApps |
| Shutter Network | Threshold-encrypted mempools and DAOs for fairness | Deployed on Gnosis; pursuing Ethereum integration for MEV-resistant workflows |
| Flashbots | FHE in the MEV supply chain (“Blind Arbitrage”) | Explore encrypted tx flow to limit MEV |
| OpenZeppelin | Smart contract security and standards; co-developer of Confidential ERC-20 Framework | Maintains ERC-20/721 standards and contributes security expertise to confidential token design |
| Circle Research | FHE-based privacy research & Confidential ERC-20 standard | Co-authored privacy framework; ensures compliance and composability in Ethereum |
| Fair Math | Decentralized “FHE Computer” + FHERMA challenges | Ethereum endpoint for settlement/coordination |
| OpenFHE | Leading open-source FHE library (BFV/BGV/CKKS/TFHE/FHEW) | Core building blocks for Ethereum privacy R&D |
If any player has been missed out, apologies — let us know and we will add them in future updates.
Use Cases for FHE in Blockchain
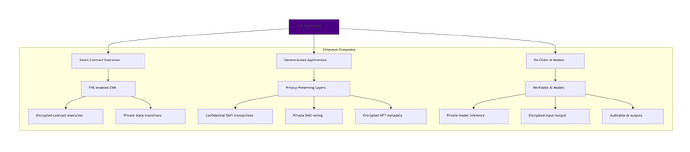
Fully Homomorphic Encryption (FHE) makes it possible to perform arbitrary computations directly on encrypted data, while keeping that data confidential at all times. This breakthrough allows users to delegate computation without ever revealing their inputs, outputs, or intermediate values. After Gentry’s 2009 result, FHE has evolved from a theoretical milestone into a technology that is finally becoming practical, with concrete implementations and rapidly improving performance. There are multiple ways this technology could fit into the Ethereum ecosystem — whether as part of smart contract execution (an FHE-enabled EVM) or as privacy-preserving layers for decentralized applications. Some of these potential use cases are outlined below.
Full list of potential FHE use cases in Ethereum and blockchain
Confidential DeFi Protocols
Private Stablecoins
What it means
Users can mint, hold, and transfer stablecoins (e.g., USDC equivalents) without their balances or transaction histories being publicly visible on Ethereum. All amounts remain encrypted, but smart contracts can still validate transfers.
Why FHE helps
- Unlike mixers (Tornado Cash) or ZK-based shielded pools, FHE allows balances to stay encrypted at all times, not just during transfers.
- Supports ongoing encrypted balance management inside a smart contract.
Challenges
- Auditing and compliance: Regulators may require “viewing keys” or selective disclosure — designing this without undermining privacy is hard.
- Interoperability: Integrating private stablecoins with public DeFi protocols breaks composability unless the ecosystem adopts privacy standards.
Confidential Lending and Borrowing
What it means
Users deposit collateral and take loans, but neither the loan size nor the collateral type/amount is visible to the public blockchain.
Why FHE helps
- Smart contracts can enforce repayment logic on encrypted balances without knowing actual numbers.
- Risk parameters (collateral ratios, liquidation triggers) can be evaluated on ciphertexts.
Challenges
- Liquidation: If collateral ratios fall, liquidators need to act — but encrypted states hide who is undercollateralized. A protocol must reveal just enough for liquidations without breaking overall privacy.
- Interest accrual: Continuous homomorphic multiplication (for compounding interest) is much heavier than additions; requires approximate schemes like CKKS, which complicates exact-value guarantees.
- Cross-protocol integration: Borrowed private assets may not be directly usable in public DeFi (e.g., using private DAI in a public AMM), limiting utility.
Private Automated Market Makers (AMMs)
What it means
Liquidity providers can contribute to pools, and traders can swap assets, without revealing pool sizes, trade volumes, or order details to the public.
Why FHE helps
- Order flow and liquidity positions stay encrypted, preventing front-running and MEV extraction.
- Pricing formulas (e.g.,
x*y=k) can be enforced over ciphertexts.
Challenges
- Computation cost: AMM math involves multiplications/divisions — costly in FHE (especially divisions).
- Slippage and price discovery: If pool states are encrypted, external actors cannot observe price changes. Some partial disclosure or oracle mechanism is required to keep markets functional.
- MEV vs verifiability: Encrypted swaps prevent front-running, but miners/validators still need cryptographic proofs (ZK or vFHE) to verify that trades followed pool rules.
- Public signals requirement: Traders and arbitrageurs need a minimum level of visibility — such as current prices, time-weighted average prices (TWAPs), or aggregated liquidity information — for markets to remain efficient. Without public signals, liquidity becomes “dark liquidity”: it exists in encrypted or hidden form, but cannot support meaningful price discovery because participants lack the information needed to quote, arbitrage, or rebalance positions.
Privacy-Preserving Governance
Sealed-Bid Voting
What it means
DAOs can conduct elections and votes without revealing individual preferences, while still proving correctness of tallies. Instead of counting plaintext ballots, the system must perform a tallying step: combining all encrypted votes into an aggregate result that can be decrypted and verified without exposing individual ballots.
Why FHE helps
- Votes remain encrypted end-to-end.
- Tallies can be computed directly on ciphertexts (e.g., homomorphic addition of
Enc(YES)andEnc(NO)ballots), ensuring no individual vote is leaked. - Only the final aggregate (e.g., “132 YES / 87 NO”) needs to be decrypted, not the individual ballots.
Challenges
- Weighted voting: Token-based or quadratic voting schemes require multiplications on encrypted values, which are more expensive.
- Central trust & key management: If a single coordinator holds the FHE decryption key, they could peek at individual votes or leak partial tallies early. A secure design requires threshold key sharing (splitting the decryption key among multiple parties) and/or verifiable decryption proofs to eliminate single points of trust.
Rollups and Coprocessors
Privacy Rollups
What it means
A rollup is a layer-2 scaling solution that processes transactions off-chain but posts compact proofs or summaries back to Ethereum for security. By batching many transactions into one, rollups reduce costs while still inheriting Ethereum’s security guarantees.
- Optimistic rollups (e.g., Arbitrum, Optimism) assume transactions are valid by default, but allow anyone to challenge incorrect state updates through fraud proofs.
- zk-rollups (e.g., zkSync, Scroll, StarkNet) require every state update to be accompanied by a validity proof (usually a zk-SNARK or zk-STARK), which Ethereum verifies efficiently.
In both designs, the rollup state (balances, contracts) is usually publicly visible.
A privacy rollup instead keeps the entire state encrypted. Users transact privately, and only encrypted state transitions plus proofs of validity are posted to Ethereum.
Why FHE helps
- Rollup operators never see plaintext states or transactions.
- End-to-end confidentiality for rollup users.
- Encrypted execution can be combined with validity proofs to preserve both privacy and trustlessness.
Challenges
- Verifiability: Fraud proofs or validity proofs must be designed to work with encrypted state transitions.
- Performance: Homomorphic evaluation of rollup transitions is resource-intensive.
- Composability: Interoperability with public L1 contracts is limited unless carefully designed.
Encrypted Execution Coprocessors
What it means
Heavy FHE computations (e.g., AI inference, simulations, or private DeFi logic) can run off-chain, with results verified and settled on-chain.
Why FHE helps
- Keeps Ethereum gas costs low by offloading complex computation.
- Enables use cases like private AI inference or encrypted simulations.
Challenges
- Decentralization: Coprocessors must not become centralized trust bottlenecks.
- Proofs: Current proof systems for verifying encrypted computations (vFHE) are immature.
- Latency: Off-chain FHE execution plus verification introduces delays compared to native EVM execution.
Use Cases for FHE and Blockchain in AI
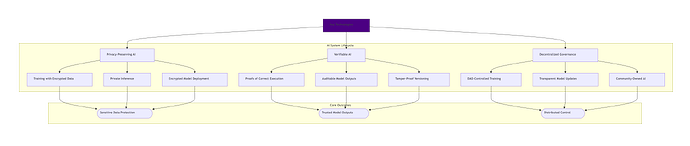
Beyond blockchain itself, the fusion of FHE and decentralized ledgers also extends into AI. The combination of blockchain and FHE can enable AI systems to be trained, deployed, and used in ways that preserve privacy, guarantee verifiability, and support decentralized governance. Such an integration ensures that sensitive data remains protected, that model outputs can be trusted, and that control over powerful AI systems does not concentrate in the hands of a few. The following sections outline potential use cases that illustrate these possibilities.
Full list of AI + FHE use cases
Privacy-Preserving AI Inference
Healthcare
What it means
Patients can query AI diagnostic models using their private health records, without disclosing the records to hospitals, insurers, or cloud providers.
Why FHE helps
- Health data stays encrypted end-to-end.
- The model processes ciphertexts directly, and only the result (e.g., diagnosis probability) is decrypted.
- Prevents leaks that arise from centralized data storage.
Why blockchain helps
- Provides an auditable log of queries and results without exposing patient data.
- Enables decentralized governance of medical AI models (e.g., deciding which hospitals or researchers may update them).
- Removes single points of trust — patients interact through open protocols, not proprietary silos.
Challenges
- Performance: Inference on deep models under FHE is still costly.
- Partial disclosure: Regulators may require selective auditability.
- Integration: Hospitals must trust that encrypted inference is correct → verifiable FHE needed.
Finance
What it means
Investors can run risk models or portfolio analyses on sensitive financial data without revealing their positions to brokers or service providers. A portfolio position refers to the specific assets and allocations an investor holds (e.g., number of shares of a stock, amount of ETH, value of bonds). These positions are highly sensitive, since they reveal trading strategies and risk exposure.
Why FHE helps
- Keeps portfolio positions encrypted while models compute performance or risk (e.g., volatility, value-at-risk).
- Enables confidential “stress tests” and compliance checks without exposing individual holdings.
Why blockchain helps
- Serves as a neutral settlement layer: the blockchain records payments, analysis requests, and results in a tamper-proof way, ensuring neither the investor nor the model provider can alter outcomes.
- Auditors can verify that models were executed according to agreed smart contracts, without relying on a central authority.
- Encourages fair marketplaces for risk models, since settlement happens on-chain rather than through a single broker or intermediary.
Challenges
- Complex models: Risk engines use heavy computations (matrix multiplications, eigenvalue decompositions), which are expensive under FHE.
- Latency: Market environments demand real-time inference, but FHE introduces overhead.
- Trust: Requires proofs that encrypted results correspond correctly to the encrypted inputs.
Verifiable AI Outputs
Auditable Financial Predictions
What it means
Regulators and auditors can check that AI models for trading, risk scoring, or credit decisions were executed correctly, without revealing input data.
Why FHE helps
- Models run directly on encrypted inputs.
- Final decisions are revealed without exposing sensitive market/client data.
Why blockchain helps
- Provides a neutral settlement layer for disputes (e.g., proving compliance).
- Makes results publicly verifiable without requiring trust in a single operator.
Challenges
- vFHE maturity: Proofs of correct encrypted inference are early-stage research.
- Scalability: Verifying many inferences at scale is costly.
Decentralized AI Governance
Collaborative Training
What it means
Multiple organizations jointly train a model on encrypted data, with governance rules enforced on-chain.
Why FHE helps
- Keeps each dataset encrypted during training.
- Prevents data leakage between participants.
Why blockchain helps
- Enforces governance rules (e.g., who can update the model, how rewards are split).
- Provides a transparent mechanism for coordination and dispute resolution.
Challenges
- Training cost: FHE training is still very expensive.
- Verifiability: Ensuring that model updates are honestly computed on encrypted data is difficult. Without proofs, a malicious participant could inject poisoned gradients or skip computation while still claiming rewards. Current research is exploring verifiable FHE (vFHE) and ZK proofs of correct training steps, but both remain at an early stage.
FHE Players in the Ethereum World
This section introduces the main actors working on FHE for Ethereum and related ecosystems. Their efforts are best understood in light of the challenges and use cases outlined above: enabling confidential DeFi protocols, privacy-preserving governance, secure data sharing, scalable rollups, and privacy-enhanced AI. Each player contributes different pieces of the puzzle — from core cryptographic libraries, to developer-friendly SDKs, to experimental rollup architectures — that together aim to make fully private, verifiable, and decentralized computation possible on Ethereum.
Full list of projects, frameworks, and libraries shaping FHE on Ethereum
Zama
- What they do: Zama builds open-source FHE libraries and is one of the leading drivers of applying FHE to blockchains.
- Core Tech:
- TFHE-rs: A Rust implementation of the TFHE scheme, optimized for fast bootstrapping and bitwise operations.
- Concrete Framework: A set of developer tools for working with FHE in production systems.
- Ethereum Context:
- FHEVM is Zama’s core product, enabling smart contracts to directly compute over encrypted state.
- Zama Protocol is live on Sepolia (and soon on Ethereum mainnet and other EVMs).
- Website: Zama.ai
Fhenix
-
What they do:
Fhenix builds tools that let Ethereum smart contracts handle encrypted data without developers needing deep expertise in cryptography. Their CoFHE coprocessor enables fully homomorphic encrypted computation with minimal friction. -
Architecture:
- CoFHE (FHE coprocessor): An off-chain service that performs homomorphic computations over encrypted values, sending results back to contracts securely. Developers interact through familiar Solidity patterns, while the heavy cryptography happens behind the scenes.
-
Ethereum integration:
- CoFHE is currently live on public testnets: Ethereum Sepolia and Arbitrum Sepolia. Developers can deploy FHE-enabled smart contracts and interact via the Fhenix tooling.
-
Note on evolution:
Fhenix originally proposed an “FHE Rollup” design, but has pivoted to a modular CoFHE coprocessor model that plugs into existing EVM-compatible chains.
Inco
- What they do: Inco is building a confidentiality layer for blockchains, powered by FHE and complementary techniques like MPC and TEEs. Their goal is to make smart contracts and decentralized applications confidential by default, while remaining interoperable with the broader Ethereum ecosystem.
- Key Features:
- Encrypted state and transactions, computed directly via FHE/MPC.
- Developer tooling so contracts can declare encrypted variables.
- Designed as a modular service, so confidentiality can be integrated into different blockchain environments.
- Ethereum Connection:
- Provides interoperability so Ethereum developers can bridge ERC-20 tokens into confidential ERC-20s.
- Positions itself as the “confidential computation layer” for the modular blockchain stack, complementing Ethereum’s role as settlement and liquidity hub.
- One of the founding members of the Confidential ERC-20 Framework, working with other ecosystem actors to define standards for confidential tokens.
- Whitepaper: Inco Protocol
Phantom Zone
-
What they do:
Phantom Zone researches and builds fully encrypted runtimes. Their flagship project, phantom, is an encrypted RISC-V virtual machine powered by their in-house FHE library (Poulpy). Developers write programs in Rust, compile them to encrypted RISC-V binaries, and execute them on encrypted inputs — with constants, instructions, and states all kept hidden. The goal is to enable arbitrary programs to run securely over encrypted data. -
Architecture:
- Poulpy (FHE Library): A general-purpose FHE library with support for scheme switching, threshold key generation, and bootstrapping.
- phantom (Encrypted RISC-V VM): Executes RISC-V binaries directly over ciphertexts, creating a new paradigm of “encrypted programs.”
- Research-driven Design: Prioritizes foundational primitives for encrypted computation rather than immediate dApp integration.
-
Ethereum Connection:
- Phantom is not an Ethereum L2 or chain, but could provide the runtime foundation for confidential execution layers that integrate with Ethereum in the future.
- Their focus is on low-level encrypted VM design, rather than Solidity/EVM compatibility.
-
Website: phantom.zone
Enclave (Enclave.gg)
- What they do: Enclave provides FHE-powered confidential computing infrastructure for Web3, with a focus on both DeFi and governance. Their aim is to make private computation a modular service that dApps and protocols can call into without needing to build cryptography themselves.
- Architecture:
- Confidential DeFi: Supports operations like swaps, lending, or portfolio management over encrypted states so that strategies, positions, and balances remain private.
- Governance with CRISP: Proposes confidential governance frameworks (e.g., CRISP – Confidential, Reliable, and Incentivized Secure Protocol) that allow encrypted voting and proposal evaluation. This ensures that voter preferences remain hidden while outcomes are still verifiable.
- FHE Coprocessors: Off-chain coprocessors perform homomorphic computations on encrypted inputs, returning proofs/verifiable results to the calling smart contract.
- Decentralized Key Management: Threshold-based schemes distribute trust across multiple parties, avoiding single points of compromise in decryption.
- Ethereum Connection:
- Targeted at Ethereum DeFi protocols that want to keep trades, strategies, or positions private without leaving the Ethereum ecosystem.
- Confidential governance modules can plug directly into Ethereum DAOs, giving projects the ability to conduct private votes with public verifiability.
- Enclave positions itself as a confidential execution layer that Ethereum contracts can call into, similar to an oracle but for private computation.
- Whitepaper: Enclave Whitepaper
Sunscreen
- What they do
Sunscreen is building a Secure Processing Framework (SPF)—a compiler and runtime for Fully Homomorphic Encryption (FHE) that lets developers “bring their own program” and deploy it across blockchains. It aims to power privacy-preserving applications like dark pools, private prediction markets, ML inference, and more, while ensuring verifiable hidden state. - Architecture
- “One (FHE) program, any chain”: Developers can write applications in Rust (or other mainstream languages), mark sensitive inputs/outputs, and let Sunscreen compile the logic into FHE-enabled code that runs over encrypted data.
- TFHE-focused compiler: Their new compiler generation is optimized for the Torus FHE (TFHE) scheme, supporting arbitrary-length computation—well-suited for dynamic and evolving applications.
- Verifiable hidden state: Enables scenarios where inputs remain confidential and outputs are selectively disclosed—for example, private double auctions where unmatched orders are never revealed.
- Ethereum / Blockchain Connection
- Designed for chain-agnostic integration, enabling confidential stateful computation on Ethereum and beyond.
- Supports privacy-preserving DeFi primitives such as dark pools and confidential AMMs, secure on-chain ML inference, and private state transitions with verifiability.
- Website: Sunscreen
Shutter Network
-
What they do: Shutter Network develops threshold encryption protocols to secure DeFi and DAO interactions via encrypted mempools and shielded voting. The aim is to reduce malicious MEV and front-running while preserving fair, censorship-resistant execution. They also offer a Shutter API for easy dApp integration.
- Website: shutter.network
-
Architecture:
- Threshold encryption with Distributed Key Generation (DKG) to keep transactions confidential until reveal/finalization.
- Shielded Trading (encrypted mempool), Shielded Voting (confidential DAO voting), and a developer-facing API.
-
Ethereum Connection:
- Deployed on Gnosis Chain; work toward Ethereum mainnet integration for MEV protection and fair ordering across EVM ecosystems.
Flashbots
- Focus area: Exploring FHE in the MEV (Maximal Extractable Value) supply chain.
- Concept: “Blind Arbitrage”
- Transactions are encrypted under FHE.
- Searchers/builders run strategies blindly without seeing plaintext.
- Decryption only after block ordering is finalized.
- Ethereum Context:
- Prevents front-running and back-running by hiding mempool contents.
- Whitepaper: Blind Arbitrage
OpenZeppelin
- What they do: OpenZeppelin is a leading provider of smart contract security, standards, and developer tooling. They maintain the widely adopted ERC-20 and ERC-721 standards and provide audited, production-ready implementations. As a founding member of the Confidential ERC-20 Framework, they are contributing to privacy-preserving tokens and confidential DeFi.
- Key Features:
- Maintainers of the canonical ERC-20/721 libraries used across Ethereum.
- Provide security audits and best practices for mission-critical protocols.
- Contributing to the design and specification of confidential ERC-20 tokens that integrate FHE.
- Bridge between established Ethereum standards and the emerging confidential token ecosystem.
- Ethereum Connection:
- Their libraries underpin most ERC-20 tokens and DeFi projects deployed on Ethereum.
- By helping standardize confidential tokens, OpenZeppelin ensures compatibility, security, and adoption across the Ethereum ecosystem.
- Website: OpenZeppelin
- Confidential Token Initiative: confidentialtoken.org
Circle Research
- What they do: Circle Research is the research arm of Circle, focused on advancing open-source cryptographic and blockchain standards. They co-authored the Confidential ERC-20 Framework, bringing FHE-powered privacy to ERC-20 tokens.
- Key Features:
- Co-authored the foundational design of confidential ERC-20 tokens that hide balances and transaction amounts using FHE.
- Proposed features such as encrypted balances, delegated viewing, and programmable transfer rules for compliance.
- Ethereum Connection:
- The Framework transforms existing ERC-20 tokens into privacy-preserving wrapped versions that remain fully composable across Ethereum and EVM chains.
- A founding member of the Confidential ERC-20 Framework, collaborating with Inco, Zama, and OpenZeppelin.
- Blog / Whitepaper: Unveiling the Confidential ERC-20 Framework
Fair Math
- What they do: A research-driven company building a decentralized FHE Computer platform for secure computation on encrypted data; also runs FHERMA challenge platform to crowdsource FHE components.
- Architecture:
- FHE Computer: Modular, decentralized execution for encrypted workloads (Application, Orchestration, Verification, Execution, Data layers).
- POLYCIRCUIT components for low-level homomorphic ops.
- FHERMA for community-led library building.
- Ethereum Connection:
- Ethereum endpoint for on-chain settlement/coordination of encrypted results.
- Encrypted analytics use cases (e.g., fraud detection) with verifiability.
- Website: Fair Math
OpenFHE
- What they do: OpenFHE is the leading open-source library for Fully Homomorphic Encryption (FHE), providing developers and researchers with standardized tools to build privacy-preserving applications. It is the successor to prior open-source projects such as PALISADE, IBM HELib, HEAAN, FHEW, and other academic efforts, merging them into a single modern platform
- Architecture:
- Schemes: BFV/BGV (exact integers), CKKS (approximate reals), TFHE/FHEW (bitwise with bootstrapping), Discrete CKKS.
- Ecosystem: Benchmarking tools, C++/Python APIs, CPU/GPU backends, hybrid MPC/ZK integration paths.
- Ethereum Connection:
- Core building blocks used across blockchain privacy research and prototypes.
- Natural foundation for zk+FHE hybrids, encrypted rollups, confidential DeFi, and ML inference over encrypted data.
- Website: OpenFHE
Comparison: ZK vs FHE in Ethereum
| Feature | ZK | FHE |
|---|---|---|
| Privacy | Inputs public; witness hidden via proof | Inputs & state remain encrypted |
| Maturity | Production-grade rollups | Testnets, prototypes, research |
| Performance | Proofs verify quickly | Bootstrapping heavy (improving) |
| Use cases | Scalability, verifiability | Confidential smart contracts, private DeFi |
| Key challenge | Prover/verifier efficiency | Encrypted eval & key management |
Potential Paths Forward
Progress on FHE in Ethereum is unlikely to come from a single breakthrough. More realistically, several lines of research and development can advance in parallel, each helping to address different aspects of the challenge. The following directions outline areas where incremental improvements could open the door to broader adoption:
-
Quantifying Overhead with Open Benchmarks:
To move from theory to practice, the community would benefit from standardized, open-source benchmarks. Measuring the overhead of running representative Ethereum workloads (e.g., a Uniswap swap, a Compound loan) under FHE can guide optimization efforts and provide realistic expectations for performance. -
Designing Sustainable Economic Models:
Making privacy usable in practice also requires viable incentives. Potential approaches include:- Token-based subsidies from protocols to offset privacy overhead.
- Hybrid models where users opt in and pay a premium for confidential transactions.
- Shared security models where decryption or verification networks are incentivized to perform honestly.
-
Advancing vFHE for Decentralized Trust:
Further work is needed to make zero-knowledge proofs of FHE execution more efficient and succinct. Public verifiability is essential in Web3, and scalable vFHE is one promising path to ensure operators cannot cheat when working with encrypted data.In parallel, Trusted Execution Environments (TEEs) remain an active area of exploration. While they rely on hardware trust assumptions and are not as resilient as cryptographic proofs, TEEs can provide shorter-term pathways to verifiability and may integrate with vFHE as a hybrid solution — balancing practicality today with stronger guarantees tomorrow.
A more detailed discussion of ongoing work and open challenges around vFHE can be found in the dedicated section below.
-
Exploring Decentralized Key Management Models:
Moving beyond fixed committees is a central challenge. Research into threshold FHE (where decryption keys are distributed among a dynamic set of parties) and Multi-Key FHE combined with proxy re-encryption could help eliminate central points of failure while keeping systems aligned with Web3’s ethos of distributed trust.Further considerations and ongoing research directions on key management and decentralization are explored in more detail in the section below.
Core Considerations
As the ecosystem experiments with different architectures for FHE on Ethereum, it is easy to get lost in performance benchmarks or niche protocol designs. But long-term sustainability depends less on short-term optimizations and more on clear design priorities that guide development across projects.
We identify four core principles: application-driven scheme choice, verifiability by design (vFHE), secure key management, and IND-CPAD-level security in Ethereum contexts. Each is discussed in detail below.
1) Application-driven Scheme Choice
Different FHE families excel at different workloads depending on latency requirements, data types, and precision needs.
- BFV / BGV → Exact integer arithmetic for settlement, accounting, on-chain rule evaluation, PIR, PSI, and private smart contract/database queries.
- TFHE / FHEW → Low-latency Boolean circuits, on-chain policy checks, and scalar evaluation of arbitrary functions using look-up tables.
- CKKS → Approximate arithmetic for encrypted analytics/ML/AI, DeFi risk modeling.
- Discrete CKKS → High-throughput exact evaluation of arbitrary functions using look-up tables (vectorized TFHE/FHEW); can be coupled with BFV or CKKS.
TFHE / FHEW
Best for
- Low-latency policy enforcement on encrypted transactions (
amount ≤ limit?,KYC passed?). - Private access control in smart contracts.
- Scalar evaluation of arbitrary functions via LUTs for immediate decisions.
- Off-chain coprocessor checks where latency is critical.
How it works
- Bit-level or small-integer processing: one ciphertext = 1 bit or up to 8 bits.
- Computation proceeds gate-by-gate (AND, OR, XOR, NOT).
- Built-in bootstrapping per gate → supports deep, decision-heavy logic with constant latency.
- Programmable bootstrapping for small integers can be used to build arbitrary computation capabilities.
Strengths
- Fast for small, logic-heavy checks.
- Exact (bit-perfect) correctness.
Limitations
- No SIMD batching — poor throughput for batched data processing (e.g., scanning entire state).
- Multi-bit arithmetic requires many gates → slower for large-scale financial computations.
- Large plaintext-to-ciphertext expansion factor: each encrypted bit inflates into a large ciphertext, creating significant storage, computation, and communication overhead. This scalability bottleneck limits applicability to small, latency-critical logic rather than bulk encrypted processing.
BFV / BGV
Best for
- Exact integer operations on encrypted balances, token amounts, counters.
- PIR/PSI for querying encrypted on-chain or off-chain state without revealing the query.
- Private settlement, auctions, and order matching requiring exact arithmetic.
- Encrypted database queries for off-chain storage integrated with on-chain proofs.
How it works
- Operates on integers modulo ( q ) in each ciphertext slot.
- Supports SIMD batching — processes thousands of integers in one ciphertext.
- Can often avoid bootstrapping by choosing parameters to match computation depth.
Strengths
- Exact, bit-perfect results — essential for financial correctness.
- Highly efficient for vector/matrix-style operations over large datasets.
- Parallelism via batching fits many blockchain data aggregation tasks.
Limitations
- Comparisons/branching logic is more expensive/challenging than in TFHE/FHEW.
- Requires parameter tuning to avoid bootstrapping in deep computations.
CKKS
Best for
- Encrypted analytics over DeFi trading data.
- Private ML/AI inference on encrypted user metrics (e.g., credit scoring).
- Risk modeling and AMM parameter optimization using floating-point–like arithmetic.
- High-throughput processing of large encrypted datasets.
How it works
- Encodes approximate real/complex numbers with SIMD batching.
- Efficient polynomial/arithmetic ops for large-scale numeric workloads.
Strengths
- Main FHE scheme for real-number arithmetic and ML/AI in general.
- Handles large-scale approximate arithmetic efficiently.
- Batching for high throughput fits analytics and ML pipelines.
Limitations
- Inexact — not natively suitable for equality checks, threshold rules, or settlement values.
Discrete CKKS
- Provides the same capabilities as TFHE/FHEW but for batched processing.
- Achieves throughput of 2-3 orders of magnitude higher than TFHE/FHEW.
- Slower than TFHE/FHEW for vectors of size up to hundreds (for small-precision operations). Faster than than TFHE/FHEW for larger vectors or large-precision operations.
- Ideal for offline batch processing of data.
Summary Table
| Scheme | Data Type | SIMD | Exact? | Best for |
|---|---|---|---|---|
| TFHE/FHEW | Booleans (bit-level) | No | Yes | Low-latency on-chain policy checks, private access control |
| BFV/BGV | Integers (mod q) | Yes | Yes | Settlement, PIR, PSI, encrypted DB queries |
| CKKS | Real/complex (approximate) | Yes | No | Encrypted analytics, ML/AI on DeFi data |
| Discrete CKKS | Integers / fixed-point (discrete) | Yes | Yes | Confidential DeFi (balances, interest, liquidation), private payments, governance voting, encrypted accounting |
2) Verifiable by Design (vFHE)
In Web3, verifiability is not optional: unlike Web2 systems, which rely on trust in centralized providers, blockchains replace trust with consensus, where every validator must independently check correctness. This makes publicly verifiable correctness a core security property.
Homomorphic computation complicates this picture by introducing a fundamental challenge: how can validators verify that an off-chain FHE computation was performed honestly? Without a solution, validators would either have to trust specialized evaluators (contradicting decentralization) or attempt to recompute heavy FHE circuits themselves. Hence the push toward verifiable FHE (vFHE).
Design options for verifiability in Ethereum:
A. Proof-carrying FHE (succinct arguments)
An evaluator returns (Enc(f(x)), π), where π is a succinct argument that the ciphertext transition matches the FHE semantics for circuit f. This mirrors zk-rollup verification: on-chain cost is the proof verification.
-
vFHE from general-purpose SNARKs (2024)
-
Zama’s vFHE bootstrapping demo (2024).
Zama showed TFHE programmable bootstrapping can be proven with a SNARK using Plonky2 IVC: ~18–48 minutes to prove, ~5–10 ms to verify (hardware-dependent). This is research/PoC, not yet a full pipeline, but demonstrates feasibility for the hardest step.
Zama blog -
HasteBoots (2025).
A purpose-built succinct argument system for FHEW/TFHE bootstrapping (ePrint 2025/261).
Uses custom polynomial IOPs plus an optimized polynomial-commitment scheme (with packing) to achieve seconds-level proving (e.g., ~3 s on Apple M4 in experiments).
No need for zero-knowledge since ciphertexts are opaque; focus is purely on correctness of the FHE relations (NTT, lifting, accumulator update, modulus switching).
Implications for Ethereum.
Proof-carrying FHE integrates cleanly: evaluators (coprocessors) post (ciphertext, proof); a verifier contract checks π and updates encrypted state.
ZK is optional here — soundness and succinctness matter most.
B. Trusted hardware attestations (TEEs)
Another approach is to execute FHE computations inside a Trusted Execution Environment (TEE) such as Intel SGX or AMD SEV. A TEE provides a hardware-protected enclave where code and data remain confidential and tamper-resistant, even against a malicious host.
When an enclave is initialized, the TEE performs a measurement: it computes a cryptographic hash (e.g., SHA-256) of the program code and critical configuration loaded into the enclave. This hash uniquely identifies the binary being executed. The hardware then generates an attestation report, which contains:
- The enclave’s measurement (the hash of the loaded code).
- A digital signature over this measurement, produced using a hardware root-of-trust key provisioned by the vendor (Intel, AMD).
The attestation can be sent alongside the encrypted computation results. External verifiers — such as Ethereum smart contracts or off-chain validator services — check that:
- The vendor’s signature on the attestation is valid.
- The measurement matches the expected reference hash (the known, vetted binary implementing the FHE evaluation).
If both checks succeed, the verifier gains assurance that the computation was performed by the intended enclave code, and that inputs remained confidential during execution. This approach avoids the need for heavy cryptographic proofs, but its security model is weaker: it depends on the guarantees of the hardware vendor and the integrity of the attestation infrastructure, rather than purely on cryptography.
C. Re-execution / redundancy
In this model, evaluators post ciphertext state updates without attaching proofs. Validators (or designated challengers) can independently re-execute the FHE computation off-chain to check correctness. If a discrepancy is found, a fraud-proof–style dispute mechanism would be triggered, replaying the computation step-by-step until the error is located.
This is essentially the optimistic rollup approach applied to FHE: correctness is assumed by default, and only verified if challenged. The advantage is minimal upfront cost on-chain — no need to generate or verify heavy proofs for every update. The drawback is that re-executing FHE circuits remains computationally intensive, and security depends on the assumption that at least one honest validator will re-run computations and raise disputes when necessary.
There is, however, an additional subtlety compared to public-state rollups. If a malicious ciphertext slips through and is optimistically accepted, a user who later decrypts it may unwittingly act as a reaction oracle. Even without seeing the plaintext, an adversary could observe how the user behaves — for example, whether they continue, abort, or fail in follow-up interactions. Because decryption in LWE-based FHE schemes ties the plaintext directly to the secret key, such reaction signals can, in principle, be exploited in chosen-ciphertext–style key-recovery attacks. This risk does not arise in normal rollups and highlights why applying an optimistic model to FHE requires particular care.
Takeaway.
For Ethereum integration, proof-carrying FHE remains the ideal long-term design: it mirrors the verification logic of rollups and ensures trustless correctness.
- Zama’s SNARK-based prototype shows feasibility, but is not yet practical.
- HasteBoots points toward a much more efficient path, especially for TFHE-style schemes.
- TEEs and re-execution can serve as interim or complementary mechanisms, but ultimately succinct cryptographic verifiability is the preferred solution that scales in a decentralized setting.
3) Secure Key Management
Secure key management is a critical pillar for the adoption of FHE in blockchain. In the blockchain context, secure key management must go beyond traditional approaches — it requires mechanisms that are resilient, decentralized, and compatible with adversarial environments. Threshold cryptography (Asharov et al., EUROCRYPT 2012), multiparty computation, and proxy re-encryption (Yasuda et al., ISC 2018) offer promising ways to ensure that no single entity holds unilateral control over decryption, while still enabling efficient and reliable operations.
Equally important is the principle of user sovereignty. Participants should be able to retain meaningful control over their keys without being forced into custodial models that undermine decentralization. Secure key management in this setting is not only about protecting private data but also about aligning with the ethos of blockchain: distributing trust, ensuring availability, and making systems resistant to both technical failures and governance capture.
Key Generation and Encryption
Managing keys begins at setup. In a threshold FHE scheme, all participants jointly run a Distributed Key Generation (DKG) protocol to produce a common public key and shares of a common secret key (Asharov et al., 2012). This means the group effectively has one FHE key pair (public, secret) that is shared – each party holds a secret share and the public key is the same for everyone. Every party’s data is encrypted under this joint public key.
By contrast, in a multi-key FHE (MK-FHE) scheme, no upfront joint key generation is required. Each user independently creates their own key pair and can encrypt data with their own public key. Homomorphic operations can then be performed on ciphertexts encrypted under different users’ keys (hence “multi-key”). The big benefit here is that parties do not need to coordinate or be online at the same time to set up a common key. Encryption can happen at any time, by any party, using their own key, which is convenient in distributed settings (e.g., users joining at different times or uploading data asynchronously). This eliminates the complex DKG step required by threshold FHE and simplifies initial key management (Chen, Chillotti, Song, ASIACRYPT 2019).
Security Risks and Protections in Threshold FHE
Two subtle challenges arise in threshold FHE schemes that connect both to key management and to the broader goal of being verifiable by design:
1. Leakage from Decryption Shares
- In threshold FHE, each party publishes a decryption share. Over multiple decryptions, these shares may leak information about the secret key.
- Two common mitigations:
- Noise Flooding (Smudging): each party adds large random noise to its share before releasing it, hiding correlations with the secret key. This requires enlarging FHE parameters to tolerate the extra noise.
- MPC Rounding: parties jointly execute a secure multiparty computation (MPC) to complete the rounding step of decryption directly on their secret shares, so that only the plaintext is revealed. This avoids parameter blow-up but introduces more MPC overhead.
2. Verifiable Key Generation
- While MPC ensures fairness and correctness among key-generation participants, it provides no guarantees to outside verifiers.
- To make the distributed key setup itself verifiable, one can use:
- Publicly Verifiable Secret Sharing (PVSS): each party’s share is accompanied by a proof that it is consistent with the committed secret, so anyone can verify the DKG.
- Collaborative SNARKs (cosnarks): participants jointly generate a succinct proof that the DKG protocol was executed correctly, offering a publicly verifiable guarantee of honest key generation.
Decryption Mechanisms
The flip side is how decryption is handled when multiple key holders are involved:
-
Threshold FHE decryption: Since there is one common secret (split into shares), parties can decrypt collaboratively. A classic threshold scheme can be configured as n-out-of-n (all shares required) or more flexibly t-out-of-n, where any subset of at least
tparties can decrypt. This flexibility is an advantage of threshold FHE – it can tolerate some parties being offline during decryption (as long as the threshold numbertcooperate).However, its security rests on the threshold trust assumption – typically that a majority of parties remain honest. If too many collude, they can prematurely decrypt ciphertexts and break confidentiality. This collusion risk is fundamental: any set of t or more cooperating parties can recover the secret key in a standard threshold scheme.
Recent work has proposed accountability enhancements to deter or detect collusion. For example, Secret Sharing with Snitching (SSS) by Dziembowski et al. ensures that any illicit reconstruction yields a publicly verifiable proof. Likewise, Chiang et al. (2021) introduce self-incriminating proofs for threshold encryption, guaranteeing that whenever decryption completes, at least one participant learns a proof of the decryption act. Such proofs act as an audit trail, deterring malicious behavior. Similarly, traceable threshold encryption (Boneh et al., 2021) endows a tracing key to pinpoint which parties cooperated in decryption.
Another well-known limitation of threshold FHE is the rigidity of fixed committees. Traditional schemes rely on a costly and communication-heavy Distributed Key Generation (DKG) ceremony. Once completed, the committee of parties is essentially fixed: adding or removing members requires running another DKG, which is impractical in dynamic blockchain settings where validator sets rotate or participants churn. Recent work on silent setup (Hall-Andersen et al., ePrint 2023/318) addresses this problem by letting each party independently generate a key and publish a small “hint.” Any subset of hints can then be combined to form a public key without global coordination. This makes committees easier to reconfigure, supports asynchronous onboarding, and reduces setup complexity from quadratic to essentially linear communication.
In short, while classical threshold FHE provides flexible t-out-of-n decryption, it inherits trust and rigidity issues: collusion can break confidentiality, and fixed committees make reconfiguration expensive. New primitives — accountability mechanisms (SSS, self-incriminating proofs, traceable encryption) and flexible setups like silent DKG — significantly mitigate these problems. For a clear applied discussion in the context of encrypted mempools, see the Shutter Network blog post.
-
Multi-key FHE decryption: The main benefit over threshold FHE is that encryption is performed using different keys (no need to generate a common joint key before encryption). The result of homomorphic computation on multi-key-encrypted data is a ciphertext that is tied to multiple secret keys.
In standard MK-FHE schemes, all participating users must collaborate to decrypt – essentially an n-out-of-n requirement by default. Each user uses their own secret key to produce a partial decryption, and these partial results are then merged to recover the plaintext. A known drawback is that this merging process requires interaction and all key holders to be online simultaneously. If even one party is unavailable or uncooperative, decryption cannot proceed. Moreover, the communication and computation cost of combining decryption shares grows with the number of parties.
In short, out-of-the-box multi-key FHE lacks the built-in flexibility of a threshold scheme’s t-out-of-n decryption – it essentially demands everyone’s participation for final decryption.
Hybrid Approaches and Proxy Re-Encryption
Recent research seeks to get the best of both worlds by combining multi-key encryption with threshold decryption techniques. One promising tool in this context is Proxy Re-Encryption (PRE), which enables ciphertexts encrypted under many independent keys (multi-key FHE) to be transformed into ciphertexts decryptable under a threshold committee’s key — without exposing the plaintext.
At first sight, one might ask: if the target committee is known in advance, why not use threshold FHE directly? The answer is that PRE offers advantages in two complementary ways:
1. Simplified key setup (even with fixed committees)
- Threshold FHE requires a distributed key generation (DKG) to produce a common public key and split its secret key into shares. DKG is interactive, fragile, and requires all parties online at once.
- Multi-key FHE + PRE removes this barrier: each user can independently generate their own key pair and encrypt immediately, without coordination. PRE later consolidates the multi-key ciphertext into one under the fixed committee’s key.
This means that even if the committee never changes:
- Users can onboard asynchronously, at any time.
- No global setup ceremony is required.
- The re-encryption burden is placed on the committee infrastructure, not the users.
2. Dynamic or flexible committees
In many blockchain contexts, decryption authority is not static: validator sets rotate, DAOs assign committees per epoch, or auditors change over time. PRE allows ciphertexts encrypted under independent user keys to be re-targeted to whichever committee is active at decryption time. This enables:
- Dynamic validator or committee rotation.
- Delegatable decryption rights (e.g., auditors, verifiers).
- Per-query assignment of decryptors.
Examples
- Single-proxy MK-PRE (Yasuda et al., 2018): Converts multi-key ciphertexts into a form decryptable by one delegatee. Lowers user coordination costs but introduces trust in the proxy and delegatee.
- Threshold Proxy Re-Encryption (Nakashima et al., SAC 2024): Splits the re-encryption capability among multiple proxies. No single proxy learns the full re-key, and only a threshold of proxies together can re-encrypt to the committee key.
Beyond Proxy Re-Encryption
Other hybrid multi-party FHE approaches also exist. Some combine aspects of multi-key and threshold schemes to improve efficiency. For example, Chen, Chillotti, and Song (2019) extended the TFHE scheme to a multi-key setting, enabling multiple parties to evaluate on data encrypted under their individual TFHE keys. Later work explored:
- Packed ciphertexts for batching, reducing overhead per user.
- Improved asymptotic efficiency for multi-key operations.
- Hierarchical hybrids, where a party could hold a threshold share of one key while also having their own key in another layer.
These hybrid approaches aim to preserve the encryption autonomy of multi-key systems (no global setup needed) while mitigating the decryption coordination problem via threshold techniques or key switching.
In summary:
- Threshold FHE is best when the committee is fixed and DKG is acceptable.
- Multi-key FHE + PRE simplifies setup (no DKG, asynchronous onboarding) and adds flexibility when committees rotate.
- Hybrid schemes more broadly explore the middle ground, showing the rich design space for secure and practical key management in FHE.
Practical Considerations and Tools
In practice, modern FHE libraries are incorporating these advances to make multi-party key management more user-friendly. For instance, OpenFHE supports both the threshold FHE model and proxy re-encryption operations for its major schemes (BFV, BGV, CKKS). This means that developers can, say, use threshold key-sharing so that a computation’s decryption requires multiple stakeholders, and at the same time employ PRE to rotate keys or delegate decryption when needed. A typical workflow might involve parties encrypting data under their own keys (multi-key encryption for flexibility), performing FHE computations, and then using a PRE step to convert the result into a common key before final decryption. In a blockchain context, such a design is very powerful: it allows participants to submit encrypted inputs independently, and later the network (or a set of nodes acting as proxies) can re-encrypt the encrypted result to a new key that a specific subset of nodes (or a smart contract) can decrypt. Proxy re-encryption thus serves as a bridge between different key domains, enabling dynamic key management – for example, automatically transferring decryption rights to a designated “result verifier” or rotating the keys for successive computation rounds.
In summary, multi-key FHE offers easier encryption key management (no joint key setup) and suits scenarios where parties contribute data at different times, whereas threshold FHE offers flexible decryption policies (e.g., tolerance of missing parties via t-of-n decryption). Through hybrid approaches like threshold proxy re-encryption, these two paradigms are increasingly being combined to leverage the strengths of each. Ongoing research and tooling improvements (e.g., in OpenFHE) continue to refine key management for FHE, making it more scalable and practical for real-world multi-party applications.
4) IND-CPAD Security and FHE
Why IND-CPAD Matters
All modern FHE schemes are IND-CPA secure under lattice assumptions, but IND-CPA ignores side-information such as:
- rare decryption errors (noise overflow), or
- small approximation differences (CKKS).
These subtle effects can be exploited by an adversary who interacts with FHE ciphertexts in practice. To capture this, Li and Micciancio introduced IND-CPAD. In this model, the adversary gets:
- encryption and evaluation oracles, and
- a severely restricted decryption oracle that only outputs plaintexts for ciphertexts whose plaintext is already known (e.g., ciphertexts the adversary created or derived).
This is not full CCA security: the adversary cannot decrypt arbitrary challenge ciphertexts. But it does reflect the real interfaces of FHE systems and captures side-channels ignored by IND-CPA. Note that it is well established that fully homomorphic encryption cannot satisfy full adaptive CCA security (IND-CCA2). In a conventional public-key encryption scheme, decryption is a “one-way” algorithm that simply recovers the underlying plaintext. In contrast, in an FHE scheme the decryption algorithm is entangled with the evaluation mechanism: ciphertexts can be transformed into encryptions of related plaintexts by applying homomorphic operations. If an adversary has access to a decryption oracle, they can combine this homomorphic malleability with decryption queries to mount attacks.
Known Attacks
- Approximate schemes (CKKS): Li–Micciancio showed that approximation noise leaks linear relations on the secret key, enabling passive key recovery.
- Exact schemes (BFV, BGV, TFHE): Cheon et al. demonstrated that practical implementations allow non-negligible decryption failure (e.g., ~2^-40). By crafting ciphertexts near the failure boundary, adversaries can detect anomalies and even recover keys.
Thus, both approximate and exact schemes can fail IND-CPAD if correctness is not essentially perfect.
Implications for Ethereum
Ethereum use cases amplify these concerns because adversaries can interact directly with FHE-powered contracts:
- Encrypted balances: An attacker sends crafted transfers that push a victim’s ciphertext close to failure. By observing abnormal behavior (reverts, inconsistencies), they can infer the hidden balance.
- Private auctions or voting: Malicious bids can cause tally ciphertexts to fail during decryption, leaking competitors’ bids or votes.
- Confidential contracts: Adversarial inputs can trigger decryption anomalies in loan approval or credit scoring logic, revealing sensitive state.
- Threshold FHE: Even distributing the secret key among validators does not help, since each participant may honestly decrypt adversarial ciphertexts — still leaking information under IND-CPAD attacks (Cheon et al.).
Takeaway
IND-CPAD is the realistic security notion for FHE on Ethereum. While IND-CPA is satisfied by all modern schemes, it misses the subtle but exploitable effects of decryption variability. Without IND-CPAD-level security (or mitigations), encrypted tokens, auctions, and private contracts risk leakage and even key compromise.
Conclusion
Fully Homomorphic Encryption promises to give Ethereum a native confidentiality layer, enabling private computation without undermining the network’s openness and verifiability. The ecosystem has already mapped out key directions — from scheme choice and verifiability to decentralized key management — but turning these into practice requires more than cryptography.
The real test lies in efficiency and economics: bootstrapping must become faster and its verifiability practical, developer tools more ergonomic, and business models sustainable enough that users see confidentiality as worth the cost. Benchmarks and open standards will be essential to guide this progress.
In parallel, FHE’s integration with blockchain points to broader horizons, especially in AI. Instead of closed services, we can imagine shared, verifiable, and privacy-preserving infrastructure, governed with the same trust-minimized ethos that shaped Ethereum.