Payload boosts
SummaryWe analyze the security against simple ex/post-anti reorgs and builder reveal/withhold safety for a PTC-based ePBS in the presence of colluding proposers, attesters and builders.
Introduction
We consider a PTC based ePBS mechanism in which a builder’s payload obtains an LMD weight boost if the PTC has voted for the presence of the payload, or alternatively, the presence of a withholding message. See section 4.2. in ePBS design constraints for an introduction to these concepts.
During a slot, two reveals and two rounds of voting happen. The CL block is revealed by the proposer, attesters in the CL committee (consisting roughly of all the active validators divided by SLOTS_PER_EPOCH) vote for it if it was timely (at SECONDS_PER_SLOT/4) or its parent if it was not. An honest builder either reveals a payload or a message saying that the payload will be withheld at SECONDS_PER_SLOT/2. A small committee (the PTC) attests for the presence of this payload/message at 3*SECONDS_PER_SLOT/4. The CL block gets a proposer boost PB if it is timely, the payload (resp. the withholding message) gets a payload reveal boost (RB) (resp. a payload withholding boost (WB)) if the PTC voted for its timelines.
We show that there exists weights for these three boosts such that the system is resilient against a collusion between two proposers against a builder or a proposer and a builder against another proposer, satisfying thus the builder safety and no ex-anti nor post-anti reorgs, if the colluding parties do not control more than 20% of the stake. We delve into relaxing the conditions for the colluding attesters in the splitting attacks to maintain a higher reorg resistance under malicious stakers, or viceversa, relaxing the conditions against malicions stakers colluding with builders by guaranteeing honest builders’ safety.
Acknowledgments I want to thank @rkapka for useful feedback.
Splitting attacks
Withholding safety
In this scenario the CL block for N has weight x, the parent block has weight 1-x, the PTC committee sees a message that the builder wants to withhold his block and it gives it weight WB. The next proposer can only force the builder to pay if
We can force the RHS to be at least \frac{1}{2} by setting
Delaying attestations.
In the same scenario as above, an attacker may want to grief the builder by not only splitting the view but also witholding attestations and revealing them later. Say the attacker has a stake of \beta, proposes slots N and N+1 and splits the view as above so that the builder sees x voting for N, 1 - x - \beta voting for N-1. An honest builder would withhold if
After the builder decides to withhold the attacker releases the aggregated attestations for N, the next proposer can succesfully force payment if
Combining this with the previous inequality we get
Which leads to
Therefore as long as WB - PB \geq \beta builder withholding safety holds.
Reveal safety
In this scenario the CL block for N has weight x, the parent block has weight 1-x and the builder has revealed his block. The next proposer can reorg the payload if
If we want to force the RHS to be at least \frac{1}{2} we need then
Delaying attestations
Similarly to above, if in addition the attacker holds a stake of \beta that is witheld during N and only revealed after the builder’s actions. The honest builder will reveal his payload if
After the reveal, the attacker broadcasts the aggregated attestations supporting N-1 the next proposer can reorg the payload only if
Combining with the above equation we get
Thus as long as RB - PB \geq \beta the builder reveal safety holds.
Post-anti Reorgs.
Vanilla post-anti reorg
The proposer and builder of N act timely and the attacker has stake \beta and proposes slot N+1, he can reorg the block if
Which is impossible given our assumption RB - PB \geq \beta.
Builder collusion
In this scenario the builder for N colludes with the proposer of N+1 in order to grief the proposer of N leveraging the withholding boost. That is, the proposer of N is timely and reveals his block. The attacker, with stake \beta votes for the parent block N-1, he is also the builder for slot N and sends a withhold message. The next proposer can reorg the block if
Therefore in order to avoid post-anti reorgs because of builder collisions we need PB + WB + 2\beta \leq 1.
Ex-anti Reorgs
Vanilla ex-anti reorg
In this scenario the attacker proposes block N late and wants to reorg N+1. He releases a block late together with attestations for it. We have seen above already that if the builder is not colluding in this attack and withholds, then the conditions for builder withholding safety by definition prevents this reorg from happening.
Builder collusion
In this scenario the proposer and builder of N are colluding to reorg the proposer of N+1. The proposer sends his block late and does not reveal the attestations until very late (say when the block for N+1 is being produced), and the builder sends his payload supporting this block. The proposer of N+1 will see the PTC vote beforehand. So assuming he has seen the PTC vote but not the attestations for it and honest validators voted for N-1, he will reveal his block based on N-1 if
After the reveal happens, his block will be reorged if
Combining with the above we get
Thus as long as PB \geq \beta, we can prevent ex-anti reorgs. That is, under the assumption of builder’s collusion, the situation reverts to the current ex-anti reorg analysis pre-ePBS.
Worst case single-blocks collusions.
The cases we have analized so far are cases in which either
- The adversary controls two blocks and wants to grief the builder of one of those.
- The adversary controls one block and a builder and wants to grief a proposer for the other block.
In addition the adversary has stake \leq \beta and and can split the view of the honest attesting committee at will.
We see that satisfying the four inequalities
We can guarantee builder safety as well as ex-anti and post-anti 1-slot reorgs.
Combining the first two equations we have
Using the last equation we get
So the best we can do is protect of all these attacks at once against adversaries with \beta \leq 20\%.
Setting \beta = \frac{1}{5} we get optimal values for PB = \frac{1}{5}, WB = \frac{2}{5}, RB = \frac{2}{5}.
Relaxing builder/proposer safety
There is no reason to guarantee safety under splitting attacks or under reorg attacks for adversaries with the same security threshold. We may for example guarantee builder safety under an adversary that has \beta_{builder} stake, and reorg safety for an adversary that has up to \beta_{proposer} stake. The above equations read now:
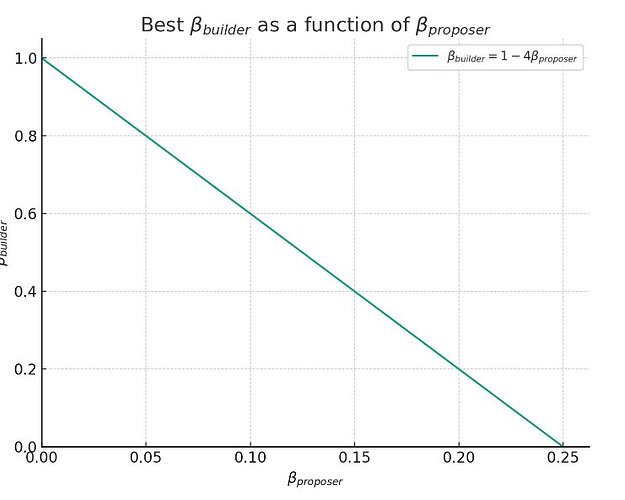
Combining the first two equations we get WB \geq \beta_{builder} + \beta_{proposer}. Using the last one we obtain
\beta_{builder} + 4 \beta_{proposer} \leq 1. It follows that for a fixed reorg security threshold \beta_{proposer}, we can guarantee builder safety for up to \beta_{builder} \leq 1 - 4 \beta_{proposer}. The value of 20% is such that they become equal, but we may be happy guaranteeing reorg safety under 22% attackers and builder safety under 12%, or conversely, if we trust the builders not colluding often (or imposing some slashing conditions) we may secure the builders under attackers that have 40% of the network giving reorg resistance only up to 15% adversaries.
Conclusions
This short note shows that we can indeed guarantee builder safety under certain forms of ePBS while maintaing all the design constraints of ePBS design constraints. Moreover, it shows that we can keep a high forkchoice safety if we are willing to guarantee builder’s safety for attackers that do not hold a large percentage of the stake.