Plasma Cash was a transaction format
TL;DR:
This post examines fungibility in Plasma Cash and how it relates to safety proofs. It first argues that one of Cash’s main innovations was to introduce coin ordering via a number line, decreasing fungbility in exchange for light client proofs and mass exit prevention. On its own, this “range-based” transaction format removes the mass exit vulnerability even with full node, MVP-format blocks.
Next, it discusses how merkle trees give blocks light client proofs, and motivates the merkle sum tree construction of blocks, which can further reduce leightweight proof size from O(log(# coins)) to O(log(# txns)).
Last, it proposes a new transaction design that can reduce RSA accumulator requirements to O(# fragments) total primes enumerated and O(1) witnesses per transaction by embedding primes into the range transactions. edit: broken, see section below
Plasma Cash → Spooky Plasma Numberline
It’s well-established that Plasma Cash’s poposal to represent coins as non-fungible tokens introduced two key improvements: light client proofs and nullifying the mass exit vulnerability.
However, it’s not ideal to interpret Cash coins as equivalent to ERC721s. In general, note that coin fungibility is not “yes/no”–for example, shielded ZCash outputs are “more” fungible than BTC/ETH, because we can trace the Silk Road coins and view ETH balances.
Another interpretation is that Cash treats coins as ranges “on a number line” instead of “in a pool” like MVP did. This will allow us to guarantee safety on subsets of exits–a particular range–even without a sparse merkle tree of NFT transactions like in Cash.
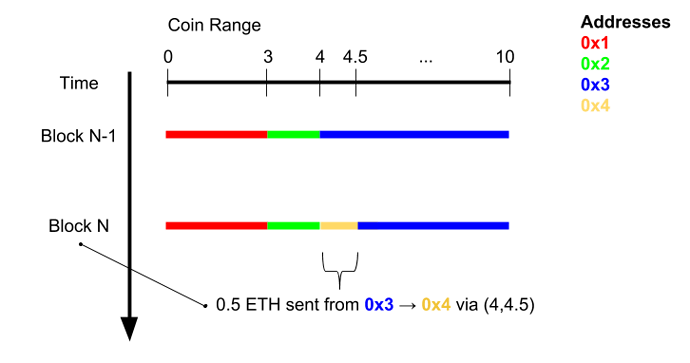
Here’s an example transaction in this model:
Here, we have a 10 ETH plasma chain where user 0x3 pays 0.5 ETH to 0x4. But, critically, it’s a “particular” 0.5 ETH: the range (4,4.5). The transaction would look something like:
-startpoint (4 in this case)
-endpoint (4.5 in this case)
-recipient (0x4 in this case)
-signature (0x3's in this case)
similarly, an exit would look something like:
-startpoint
-endpoint
-claimant
This interpretation welcomes a family of proof schemes including light client structures. But even before we get into any merkle business, have a notable improvement…
Ranges to the rescue: no more MVP mass exit vulnerability
In plasma MVP, the operator could create an invalid (“out-of-nowhere”) transaction, and use the UTXO to create an invalid exit. This exit is not properly challengeable because its (invalid) history is withheld. The original solution forced all users to speedily exit the contract themselves, before the unchallengeable exit got the chance.
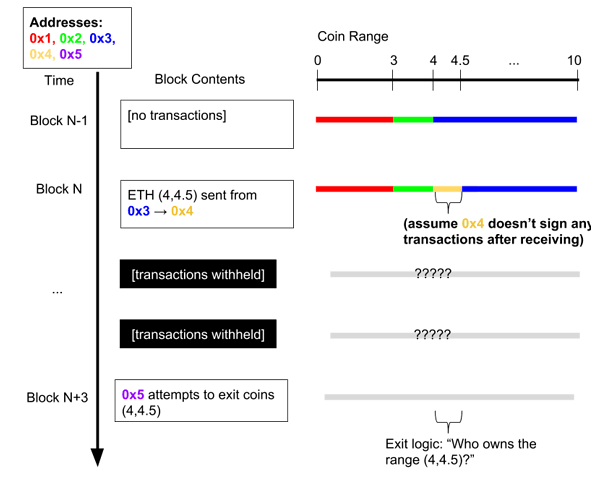
Using the range interpretation is a way to avoid mass exiting; the operator will no longer be able steal funds. This time, they are forced to specify the range they’re trying to exit, allowing the rightful owner to challenge with ownership proofs. Here’s an example:
In this example, 0x5’s wrongful exit can always be challenged by the rightful owner, 0x4, by pointing to the transaction in block N. When 0x5 can’t respond by showing that 0x4 spent the output, the exit is cancelled.
The problem with MVP was that nobody in particular had the responsibility to challenge an “out of nowhere” spend. In this model, someone always does–the range’s true owner.
How merklizing by range makes thin clients
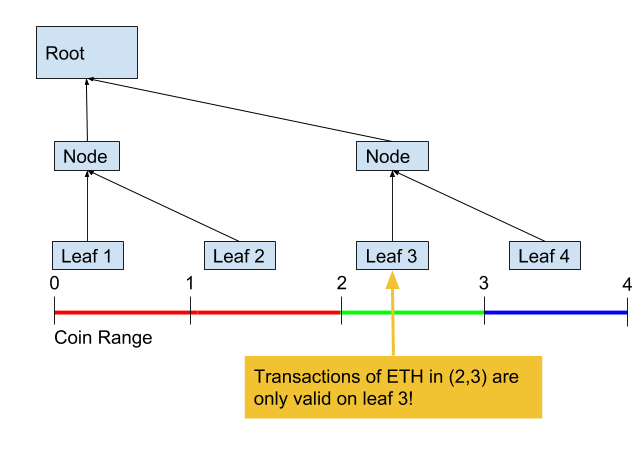
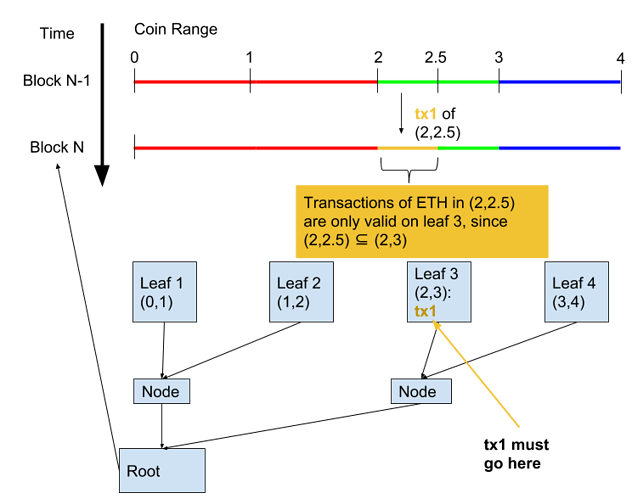
The other thing Cash introduced was lightweight proofs. This allows users to confirm safety without downloading an entire block, because transactions of a certain range are only valid on a certain branch:
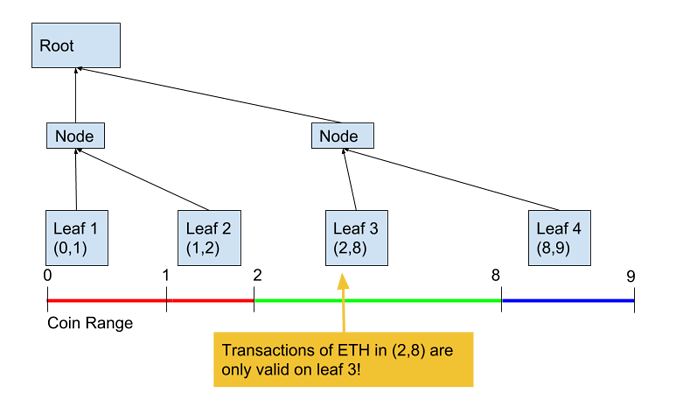
The merkle branches are like “monitors” over particular ranges of transactions. The branches aren’t coins; the ranges below them are. Notably, there’s no particular reason they have to be equal “denominations.” Imagine this example:
It wouldn’t do much, but we could still construct a valid exit game with unequal branch sizes.
Something we might ask is: what if a transaction and a branch have different ranges? In Cash’s original specification it simply couldn’t, the transactions had fixed denomination. But reusing the range-based transaction format from above, we can validate any size payment:
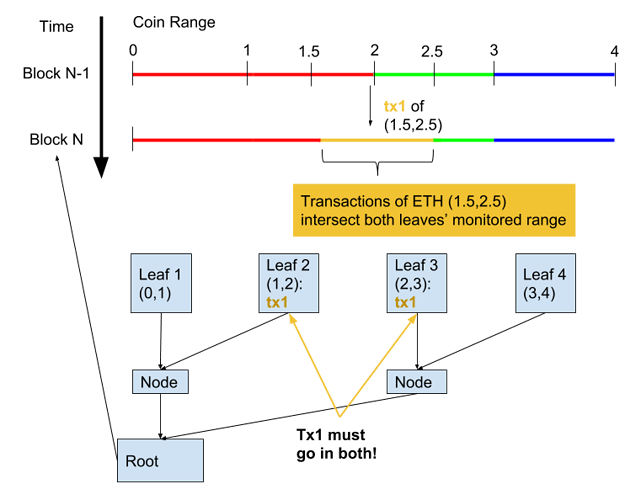
Even if a transaction overlaped multiple branches, we could maintain safety by requiring such transactions to be included in both:
With this in mind, “arbitrary denominations” in plasma cash are more manageable than thought. However, the overlapping is still problematic; in this example we were forced to download the whole tree. We could prevent overlapping if each branch covered specific transactions…
Merklizing addition for thin and profit
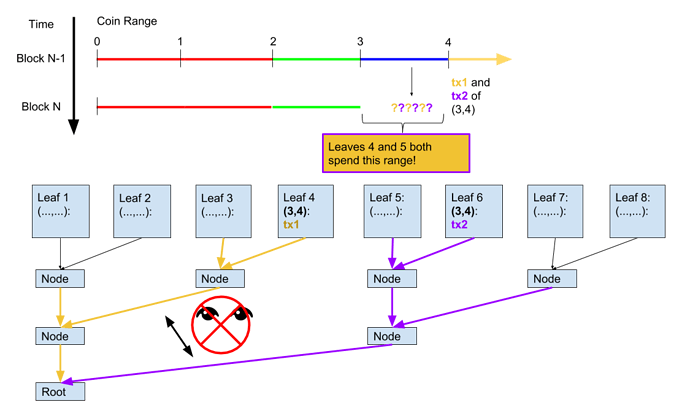
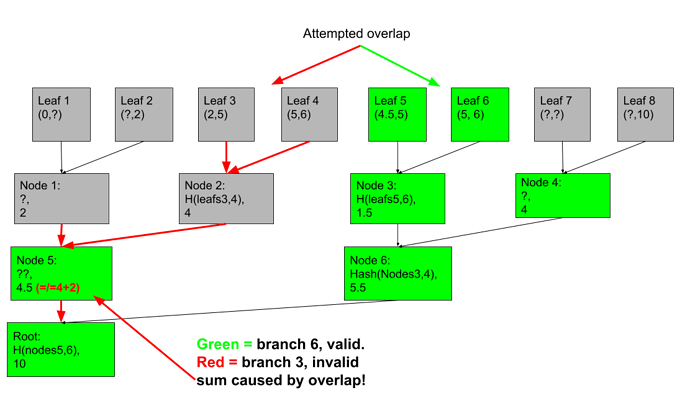
If we just allowed branches to monitor arbitrary ranges, a problem would arise from not seeing what’s in the other branches. The operator could double spend two branches with an overlap:
The only way for yellow or purple clients to know of the other transaction is to download the opposite colored branch–but they don’t know it’s there! So clients would have to download every single leaf to check for double spends…no more light clients.
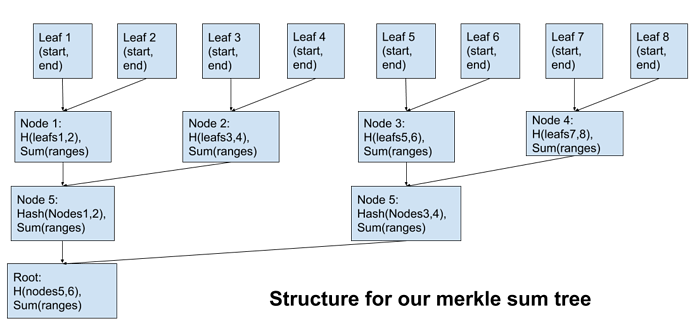
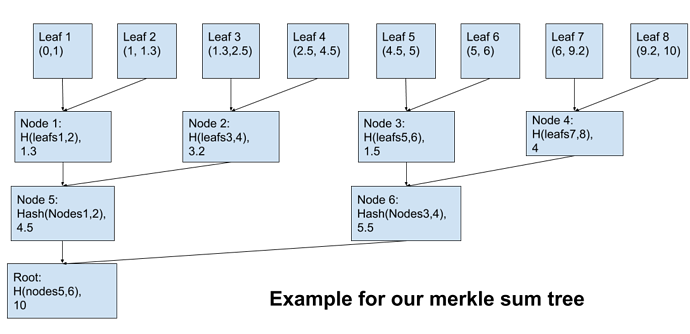
As it turns out, we can bring the light proof property back by modifying the tree structure. Now, instead of a plain merkle tree, we use a sum tree to encode more info into branches:
As an example:
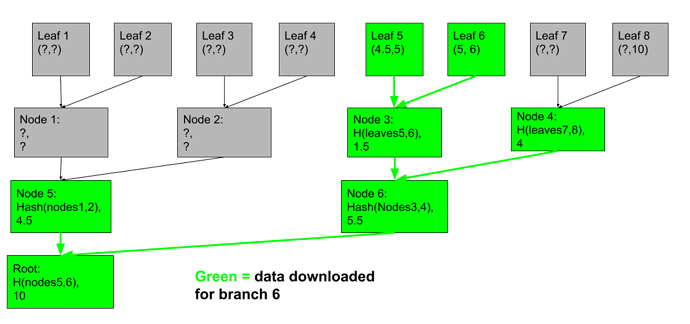
In this structure, each merkle node sums up the total range covered by its two children. We can now take a single branch, use it to total up the ranges to the left and to the right, and verify that they agree with our own ownge. Go ahead, try to “trick” leaf 5 or 6 by making another branch that intersects the range (4.5,6). Filling in only the ?'s in grey boxes:
With a few tries, you’ll see it can’t be done anywhere without changing the sum at one of the green nodes.
Thus, using only the green branch, we can be confident that no valid, intersecting branches exist.
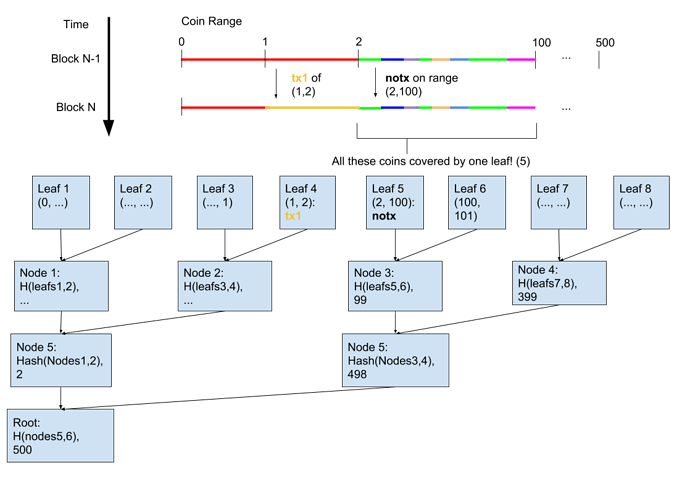
This construction can conver vast swaths of unmoved coins with a single no tx branch covering their wide range:
In the worst case, if every transaction is separated by untouched coins, the number of branches needed would be just twice the number of transactions. This is comparable to needing as many branches as coins in fixed-denomination Cash. It’s reasonable to assume coins are transacted much less frequently than once-per-block, so a branch size decrease from O(log(#coins)) to O(Log(#transactions)) might increase throughput significantly.
note: The sum construction (and many conversations that influenced this post) stemmed from the Plasma Cashflow doc last month.
Cheaper RSA
Edit: this scheme was discovered to be broken, see discussions here. With this realization, I believe vector commitments may be the best way to develop a scalable succinct proof scheme.
Using a secondary cryptographic accumulator which also “watches” coins is a promising way to prevent coin histories from growing linearly in blocks, by using succinct non-inclusion proofs instead of downloading empty (notx) branches.
Previously, the bottleneck for RSA accumulators was that each Cash coin required its own prime number to (dis)include from the accumulator each block. This requires a huge amount of prime numbers–restricting the coin carrying capacity by how many primes can be enumerated and the transaction capacity by how many witnesses can be calculated. Vitalik found an awesome way to reduce the witness computation, but this still requires us to enumerate O(N) primes, one for each Cash coin.
Not unlike the sparse tree, these constructions were cumbersome because the range which each prime covers is stuck, fixed at the smallest denomination. We can construct a scheme where the primes cover varying ranges, like the merkle sum branches do.
The trick is to point each transaction to particular primes. Now, valid transactions include a new prime, which must be witnessed in the RSA accumulator on the next valid spend of that coinrange. This way, different transactions can point to the same prime, and share it as a “monitor.” The full transaction format would be:
-startpoint
-endpoint
-newPrime
-recipient
-signature
With the condition that a new transaction intersecting (startpoint, endpoint) is only valid if the newPrime listed by its previous owner was included in the RSA for that block.
This might introduce a small coordination cost, but it also reduces the RSA bottleneck significantly. The right strategy could limit the number of primes enumerated to the number of fragments or lower and support O(1) inclusion and non-inclusion proofs for dynamic ranges.
General Tradeoffs
The goal of this post was to present a different way to think about Plasma Cash, imagining deposited coins as ranges on a number line. These safety mechanics, not just the merkle tree structure, allow for a strong design space with light client proofs and mass exit prevention.
While I think the constructions above are generally worthwhile, they do add complexity. The exit games now have to compute logic about ranges and their intersections. Also, the merkle sum structure requires extra gas to validate, though it’s also over a shorter merkle branch. It’s possible that a coarse-grained merkle tree would afford most of the same benefits in practice. Also, all of these schemes require range defragging to prevent dust, like we need for plasma Cash. This requires coordination around specific atomic swaps.
Lastly, privacy worsens when sharing ranges or primes–you leak more information to your neighbors compared to the uniform tree constructions. However, I think that privacy should be added separately to plasma rather than at the cost of performance. Lots of ZK crypto could add this–as one example, TumbleBit-style blinded mixing during defragmentation. Adding performance will eventually increase privacy by allowing more users to share the same anonymity blanket.