Plasma Cash with smaller exit procedure, and a general approach to safety proofs

[ldct]

tldr: Based on a comment by @MaxC here (Plasma Cash: Plasma with much less per-user data checking - #18 by MaxC) we can design down a version of plasma cash with a simpler exit procedure.

Motivation

The new protocol reduces the worst-case number of merkle branches checked on-chain from 4 to 3. In addition, the safety proof is easier to write in a way that generalizes to different designs, eg with splitting and merging.

Specification

To recap, tokens are indivisble and cannot be merged, transactions represent change in coin ownership and are stored in a sparse merkle tree whose root is comitted to the plasma contract. A mapping coinid => denomination is maintained in storage. Deposits create a new block with a single transaction and update the mappings. So far, this is all identical with the original plasma cash design.

We include the additional feature that transactions must commit to a specific block number in which to be included. The client must ensure that before signing a transaction whose block commitment is n, he must have validated all blocks before n (i.e., with block number < n).

The new exit procedure is:

1. Anyone can exit their coin by providing the last transaction in their coin’s history, say C, which consists of a coinid and a block, with the block being later than the coin’s deposit
2. An exit can be challenged in two ways: i) by providing a proof of a transaction spending C, or ii) by providing a transaction C* in the coin’s history before C
3. A type (i) challenge cancels the exit immediately. a type (ii) challenge can be cancelled by providing the direct child of C*.

Coin Fork Choice Rule

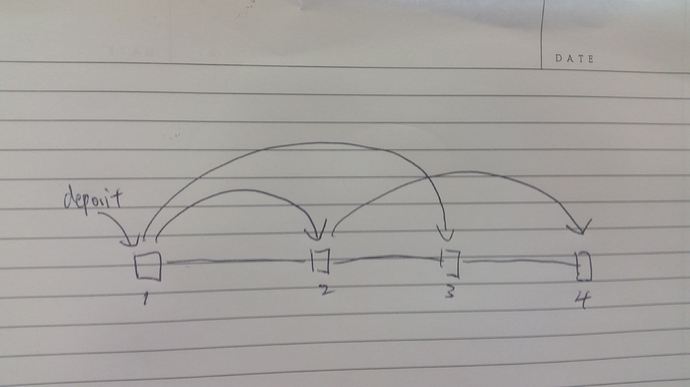
Define the coin fork choice rule (CFCR) as a function from the current state of all committed blocks to the coin that can be withdrawn. We immediately see that the new CFCR is different than the original one. For instance, given this set of transactions,

The new CFCR specifies that block 3 (and only block 3) can be withdrawn, whereas the original plasma cash CFCR chooses block 4. Even more interestingly, given this set of transactions,

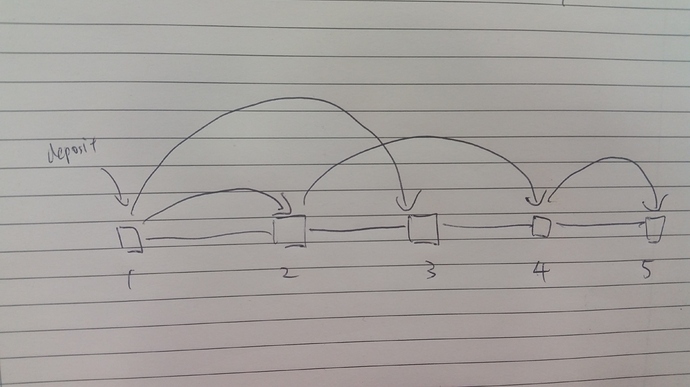
The new CFCR chooses block 3, whereas the original plasma cash CFCR returns the empty set (i.e., every exit can be successfully challenged!)

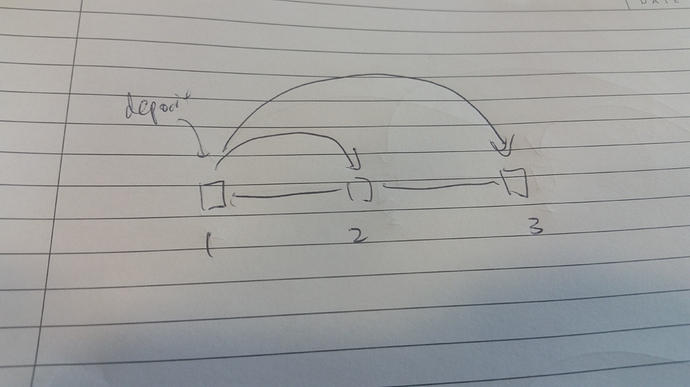
An important example to check is this one.

Both the old and new CFCR chooses block 2. Any CFCR that does not return 2 is unsafe.

Safety Proofs

Even though we defined the CFCR in terms of the exit function, it is actually easier to define the CFCR on its own using just graph-theoretic concepts. For example, the new CFCR can be specified as:

Leftmost Unspent CFCR: Return the leftmost vertex v such that there does not exist an edge vw from v to another node.

Then, a safety proof involves proving four things:

1. (exiteable): if a coin returned by the CFCR is exited, the exit cannot be cancelled
2. (no other exits): if a coin not returned by the CFCR is exited, the exit can be successfully challenged and cancelled
3. (existence of validity proof): if a CFCR returns c on a given transaction graph and the owner of c does not spend c, then the CFCR still returns c on any later transaction graph
4. (atomic transferability of ownership and validity proof): when spending a coin, if the sender and receiver both follow the proper client procedures (eg validate all blocks < n before signing a transaction spending n) then the transfer is atomic in the sense that after the transfer, one of the sender and receiver can exit the coin. in addition, this can be done in a small number of attempted exits (in both original and new plasma cash, this number is 2).

The nice thing is that this safety proof format works for proving the safety of this design, of the original plasma cash, and of designs with splitting. In addition, you can “derive” the exit procedure from the CFCR, which is nice, since in my preliminary work on writing down and exit procedure and safety proof for various designs with both splitting and merging, it appears that they become quite complicated. More details in an upcoming post.

Karl’s CFCR

In Plasma Cash Simple Spec and in a plasma call, @karl asked if it were possible to design a scheme where users can spend their coin even when block withholding is going on. This involves weakening the client procedure. We can come up with a CFCR that allows clients to do this:

Greedy Leftmost Spend CFCR: Starting from the deposit transaction, recursively find the leftmost spend of a coin. In more detail: let the transaction graph T be a directed graph over a prefix of the natural numbers, with 1 representing the block containing the deposit transaction. Define d: V(T) \to 2^{V(T)} as d(n) = \{m \in V(T) : nm \in E(T) \} (that is, the neighbours of n downstream from it). Define f: V(T) \to V(T) by f(n) = n if d(n) = \{\} and f(\min(d(n))) otherwise. Then the CFCR is f(1).

This satisifies both (3) and (4). Hence we have reduced the problem to a “purely graph theoretic” one of: design an efficient exit procedure that exits a coin if and only if it is the output of this CFCR. So far, I have tried to come up with an exit procedure that does this in a constant number of moves, but have been unable to do so.

[danrobinson]

@ldct

• Anyone can exit their coin by providing the last transaction in their coin’s history, say C, which consists of a coinid and a block, with the block being later than the coin’s deposit

Can you adapt this design so that the initial exit attempt only requires declaration of a coin ID and withdrawal address (and maybe block number), as proposed in Optimistic cheap multi-exit for Plasma (Cash or MVP)? That reduces the information necessary for an multi-coin exit in the happy case to a list of integers, which can sometimes be compressed to as little as 1 bit per coin or less.

@ldct

The new CFCR specifies that block 3 (and only block 3) can be withdrawn, whereas the original plasma cash CFCR chooses block 4.

That would mean that coin 2 needs to have the entire future of their coin, up to block N - 1, before they can authorize a transfer in block N, right? That seems pretty inconvenient. In particular, it puts a bottleneck on new block creation—the block operator needs to propagate block N - 1 to every transacting party, and they need to validate it before authorizing their transaction for block N. This is sort of like requiring preemptive confirm signatures.

I do agree there are catches inherent in the original Plasma Cash fork choice rule, although I think they can be solved using mechanisms like Reliable Exits of Withheld In-flight Transactions ("Limbo Exits").

Finally, does this even solve the problem of limbo exits? If Alice authorizes a transaction to Bob in block N, and the operator withholds block N from them, they don’t know if it’s safe to exit from Alice’s coin (and don’t have a valid proof to allow them to exit from Bob’s coin even if it is included in block N).

[ldct]

Thanks for the comments!

@danrobinson

Can you adapt this design so that the initial exit attempt only requires declaration of a coin ID and withdrawal address (and maybe block number), as proposed in Optimistic cheap multi-exit for Plasma (Cash or MVP)?

Yes, you can use the exact same technique

That would mean that coin 2 needs to have the entire future of their coin, up to block N - 1, before they can authorize a transfer in block N, right?

Yes - this is stated as a client rule in the specification

The client must ensure that before signing a transaction whose block commitment is n, he must have validated all blocks before $$n (i.e., with block number <n).

wrt:

it puts a bottleneck on new block creation—the block operator needs to propagate block N - 1 to every transacting party, and they need to validate it before authorizing their transaction for block N.

That is a disadvantage of this design, although I don’t think it creates a bottleneck, since it increases the computation and bandwidth load on the block producer, but does not asymptotically increase the expected computation and bandwidth load on the client. There is a new requirement that to spend some money the user’s client has to extend his validity proof right to the chain tip. However, in the old design, if a client had a not-so-up-to-date validity proof, yes he can still spend a coin, but the receipient has to update the coin validity proof by checking every block until he finds one that has the transaction. So in terms of the bandwidth/computation requirement of extending a coin validity proof, the new scheme is worse off by a constant factor of 2.

There’s another disadvantage that I didn’t point out in the OP - if there’s a functioning plasma fee market and a sender wants to save on gas (i.e. the equivalent of going to ethgasstation and using the SafeLow fee) he has to keep signing transactions for say a half hour.

If Alice authorizes a transaction to Bob in block N, and the operator withholds block N from them, they don’t know if it’s safe to exit from Alice’s coin (and don’t have a valid proof to allow them to exit from Bob’s coin even if it is included in block N).

That is correct, and included in the definition of atomic transferability of ownership and validity proof. One thing to note is that the limbo exit technique can be incorporated here as well. However, the design is not designed to solve the problem where the operator withholds block and there are many possible committed transaction graphs. I think solving it requires fair exchange (of transaction signature for inclusion in a block), which can only be partially done for e.g. by a commitment from the operator that is enforced on ethereum either in a state channel or out of a shared bounty contract (to be written up). Another is that I do not think the assumption made in Reliable Exits of Withheld In-flight Transactions ("Limbo Exits") that every attempted exit include a slashable/claimable bond is an optimal assumtion - I think a better way might be to have every cancelled exit not give up the bond “by default” and use revocation signatures to allow potential griefers to expose themselves to slashing (to be written up). A third thing to note is that a big problem with confirmations is that it makes it not possible to do general conditional pa (eg paying for fees in plasma MVP using an extra output UTXO) because the plasma chain execution VM can enforce atomic execution of a transaction but not fair exchange of the requisite confirmations. I think we don’t see this problem in plasma cash yet because no designs so far have any conditional payment features, but we will see them once we build more richly-featured plasma cash specs, and limbo exits won’t help solve this.

[kfichter]

This is cool, I like it.

It limits the tx timeout to a single block, but that’s probably fine. Usability might be a nightmare if blocks are full (as you said). Especially since sender needs to be online and continuously validating up to the latest block. I have to think about it more.

There’s also a weird case where a client can screw up and lose coins (is no longer left-most unspent). I’m 99% ok with this, it’s unlikely to ever be an issue and there are easier ways to lose coins.

I don’t necessarily see the “propagate block N-1” thing as a bottleneck - isn’t that already (sort of, not really) required in the original design? I guess in the original design you can just validate up to the last valid presented TX, submit the tx, see if operator rejects, validate afterwards if operator accepts, so not really.

[ldct]

Thanks!

@kfichter

there are easier ways to lose coins

I think the greedy leftmost spend CFCR is the only way to never lose coins (i.e., have no prohibitions on the client)

[danrobinson]

The safest and fairest coin choice rule, in my view, would seem to be “the last coin which has no invalid transactions in its history is the current state of the coin.” In addition to preventing the bottleneck problem, this also feels like it would adapt better to more complex coin permissioning and state transitions.

I think there is a constant-size game that lets you prove this rule is satisfied. Roughly (and this can be optimized and simplified I suspect):

1. An exit can be challenged in one of two ways: i) by providing a proof of a transaction C+ spending C’s output, or ii) by providing a transaction C- in the coin’s history that is before C’s parent.
2. A type (i) challenge can be cancelled by providing an invalid transaction in between C and C+ (thus showing that C+ does not have a valid history). A type (ii) challenge can be cancelled by providing a valid spend of C- that is before C+ (thus showing that C- is not the last valid coin in the history).

[ldct]

Yes, I think this is a valid CFCR (if I understand it correctly). For instance, in this case,

https://ethresear.ch/uploads/default/original/2X/d/d296ef0f41045906392cd8502f07c77104de0410.jpg

this rule would return 2, right?

[danrobinson]

Yep—in fact, it returns 2 for all of the examples shown above.

[ldct]

Yeah - I am amazed that in the first diagram, there are reasonable CFCRs that return 2, 3 and 4. I hadn’t considered 2 before.

Coincidentally I was talking to someone from NUS about Plasma Cash today, and he also said that he would choose 2 in the diagram. His intuition was that it analogous to git’s merge resolution algorithm which rewinds to the latest conflict-free commit.

I’ll definitely spend some time thinking about that exit game and if this generalizes easier to more complex plasma cash features.

[danrobinson]

@ldct

I’ll definitely spend some time thinking about that exit game and if this generalizes easier to more complex plasma cash features.

The kind of feature I’m thinking about is something where someone has the authority to make some change to a coin’s state, but does not have total and sole control of that coin. For example, if Plasma Cash were to implement any feature that enabled “vaults”, the hot key would have the ability to move the coin into a “pending move” state, but that move could be cancelled by the owner of the cold key. (The details of the vault and its timeout aren’t relevant to this—just the idea of one key that can update a coin’s state in only limited ways).

Suppose in the first diagram above, the coin in block 1 is controlled by Bob, and the coin in block 2 is a vault where Bob has the hot key (but Alice has the cold key, and thus would be able to cancel any move). Bob (with the cooperation of the chain operator) could jailbreak this coin from the vault, by double-spending the coin from block 1 to himself (creating the coin in block 3), and then spending the coin from block 2 to move it into a “pending move” state (creating the coin in block 4). Under your CFCR, he would then be able to withdraw the coin from block 3.