Thanks to Ben Jones, Jinglan Wang, Mark Beylin and Xuanji Li for comments.
A key component of Plasma security is an exit game, where child chain exits/withdrawals are subject to a challenge period. Upon submitting an exit, users post exit bonds that are slashed if their exits are invalid and have been successfully challenged with a fraud proof.
It’s in a user’s best interest to watch and challenge exits that impact her funds. However, it’s unrealistic that every user will operate a full Plasma node to watch and challenge relevant exits and thus to ensure all funds on a Plasma chain are secure, watching and challenging of others’ UTXOs/coins must be sufficiently incentivized.
As mentioned in Challenge Bond Pricing Concerns a few potential issues with challenge economics are:
- Lack of incentives for watching and challenging others’ transactions and coins
- High congestion from simultaneous challenges
- Increased gas cost g from increased volume (congestion)
- Poor user experience if Plasma bonds b are priced too high
- Frontrunning
To mitigate some of these concerns, a potential solution could be to create a channel auction for challenges, between the gas for challenging and bond slashing.
Channel Auctions
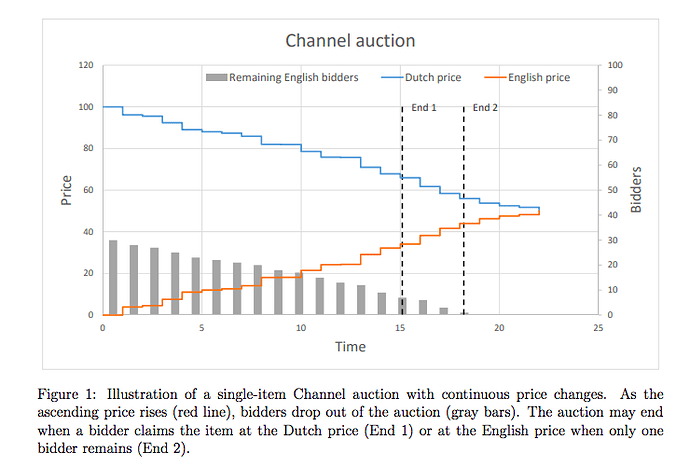
A channel auction is composed of upper-bound and lower-bound prices that eventually converge to an equilibrium price. Proposed by Azevedo, Pennock and Weyl a channel auction consists of a dutch auction (decreasing price) and english auction (increasing price) that create a channel. (1)
Bidders strategically watch the auction and either bid at the lower-bound price at which supply is still available or can accept the upper-bound price at any time. The example used in the paper is eBay’s implicit channel auction, where the “Buy it Now” price is the dutch declining price auction (although the price may remain constant or only incrementally decrease), and the sale of the item is by English auction.
In its most basic form, channel auctions produce benefits like efficient information acquisition, bidders know the maximum price they can pay for an item, and they’re always incentivized to remain in the auction if the lower-bound price is below the price at which they truly value the item.
Challenge Auctions
A channel auction-like mechanism is proposed to incentivize challenging. Where the dynamics of two heterogenous narrowing auctions create a positive externality for challengers (reward) with the upper-bound being the slashed bond and the lower-bound as the gas cost for challenging.
Whereas the paper focuses on dutch and english auctions, where the bidder (buyer) chooses which price she pays; in a challenge auction we propose two english auctions that eventually could converge, where the bidder (challenger) buys the challenge at the minimum reward (profit) she is willing to accept (the difference between the auction prices).
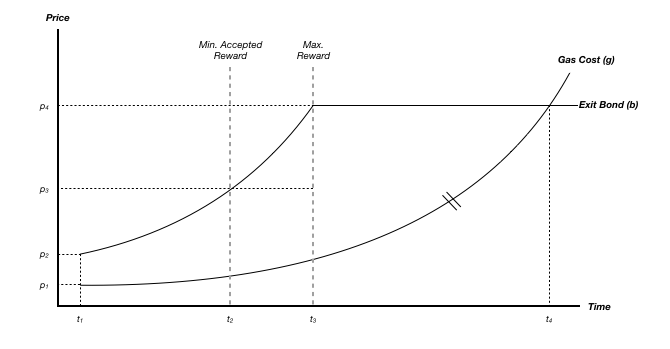
The upper-bound auction is the contribution of the user’s exit bond to a challenger’s reward (slashing) and it rises at an increasing rate as the auction continues. The gast cost per challenge is the lower-bound auction and remains constant or eventually rises as time goes on. (The assumption is that miners may begin to raise fees as auction settlement is prolonged; as the profit margin for challengers rises or if there’s increased demand in the case of many unsuccessful challenges prior to a successful challenge.)
The clearing price is a function of current miner fees, a slashing rate (potentially tied to other metrics), the size of the bond and how challengers value themselves; thus reducing the need for a pre-defined reward pricing mechanism. We can begin the auction either where r = 0 or at a p2 with minimum reward m where the curve of the bond slashing begins at r >= m.
The auction may eventually converge at the equilibrium where b = g and r = 0, at p4 (bond ceiling) where 100% of the exiter’s bond is slashed. Although the converging price dynamics are what define the “channel” part of the auction, whether or not b = g at t4, may not be relevant as we can assume that at least one challenger will buy the challenge at or before the maximum potential reward at t3.
In simple auctions (e.g., single, indivisible item auction), it is believed that rational bidders will clear the market at the second highest price, when there is only one bidder left who values the item the most. (2)
In a challenge auction, the bidder would theoretically accept the second lowest profit margin when there remains only one bidder who values the item (the challenge) the most. A challenger could accept only a reward that covers the gas per challenge (this is similar to a bidder accepting the highest cost in a simple auction), or she could wait until some level of profit let’s say at p3 and t2.
This creates a scheme where the challenge is allocated to the bidder who accepts the minimum market rate for challenges. However, the minimum reward she accepts will be equal to or less than the minimum reward that at least one other challenger would accept, as the auction is cleared upon a single successful challenge. A bidder must be strategic to both be the successful challenger and maximize her reward.
Implications
This creates a game that may reveal accurate pricing of challenges. A challenger must estimate:
-
The minimum reward she will accept to challenge exits of other users’ UTXOs/coins
-
The minimum reward at least one other challenger will accept
-
The rate at which gas will rise
-
The slashing rate of the user’s bond (e.g., if it’s dynamic to other network metrics)
Challengers are not incentivized to challenge immediately as it is beneficial to wait and optimize reward. Yet they may still rush the auction as the benefit of winning a challenge for any reward is better than winning no challenge at all. This mechanism may also reduce congestion of simultaneous challenges as the minimum accepted reward may differ per challenger, depending on their risk appetite and valuation.
Front-running could also be reduced as it would only be financially beneficial if the reward is greater than the incremental cost of front-running (e.g., incremental gas).
Collusive challengers may attempt to optimize their reward until a certain bond slashing price (how much they want to punish bad exiters), but this coordination may never happen because prisoner’s dilemma.
Other Considerations
In this analysis, we assume that any challenge is “successful” and a valid fraud proof is provided. However there may be other impacts depending on how many unsuccessful challenges have been committed (e.g., gas cost would most likely rise with increased demand).
As well, in the occurrence of simultaneous challenges, the g in our equation could be the sum of all gas used by all challengers, not only the cost incurred by the winning challenger. This would add a 5th dimension where challengers must not only estimate the expected gas but the frequency of unsuccessful or simultaneous challenges.
Ultimately we don’t want to delay the challenging of invalid exits as this puts Plasma funds at risk, although we can imagine that the auction’s duration is relative to the timing of a safe challenge period. It is also likely that at least one challenger will successfully challenge prior to the auction reaching maximum reward yield or auction time-out.
More research must be conducted on the dynamics of dual, heterogenous english auctions that converge at the upper-bound auction’s price ceiling. As well as whether a competitive challenge auction is optimal to incentivize challenging of others’ exits. Much feedback welcome.
Sources:
(1) Azevedo, Eduardo M. and Pennock, David M. and Weyl, Eric Glen, Channel Auctions (August 30, 2018). Available at SSRN: https://ssrn.com/abstract=3241744 or http://dx.doi.org/10.2139/ssrn.3241744
(2) Vickrey, William. “Counterspeculation, Auctions, and Competitive Sealed Tenders.” The Journal of Finance, vol. 16, no. 1, 1961, pp. 8–37. JSTOR, JSTOR, Counterspeculation, Auctions, and Competitive Sealed Tenders on JSTOR.