(Prerequisite : RSA Hash accumulator for arbitrary values, RSA Accumulators for Plasma Cash history reduction)
Plasma Cash flavors are suggested to use RSA accumulators to make it easier to proof the full history of a coin.
We could use the RSA hash accumulator to make this even easier, because we can include the full history of all coins in the accumulator. The hash of every transaction is stored in the accumulator and using a single witness we can show that a given history is complete.
We will use the RSA accumulator to store a matrix of values as described here. We will have one row per coin and one column per block. This will be a sparse matrix, the hash of empty spots will be set to zero, so we can ignore them in the accumulator and the witnesses.
Using the witnesses W_p and W_q we can proof on chain that a transaction is included. This is needed when there is an exit or a challenge of an exit.
W_p for a transaction contains information of all other transactions of the given coin. W_q contains the information of all transactions of all other coins. To proof that a given history of transactions of a coin is complete we only need W_q and we can show that a given history of a coin is the complete history of the coin.
Updating the accumulator
We have to make sure the plasma operator cannot update the accumulator in such a way that history is altered.
Therefore we will use the following update rule that is executed on chain.
A_t = A_{t-1}^{p_t}U_t
And the operator has to show using a Wesolowski proof that U_t is of the form U_t = g^{\alpha \prod\limits_{\substack{k=1}}^{t-1} p_{k}} \mod N
A_{t-1} is raised to the power of p_t to make sure the old transactions can not interfere with the added transactions. U_t must contain all previous primes to make sure it can not interfere with the old transactions.
Updating the witnesses
The operator has to update all witnesses W_q for every coin after every block and send them to the clients. To do this efficiently the operator can use an algorithm that uses O(n \space log \space n) time and a lookup table on disk of O(n \space log \space n) size where n is the number of coins.
We start with an algorithm that builds the witnesses for just the coin dimension, that can later be adapted to include the time dimension.
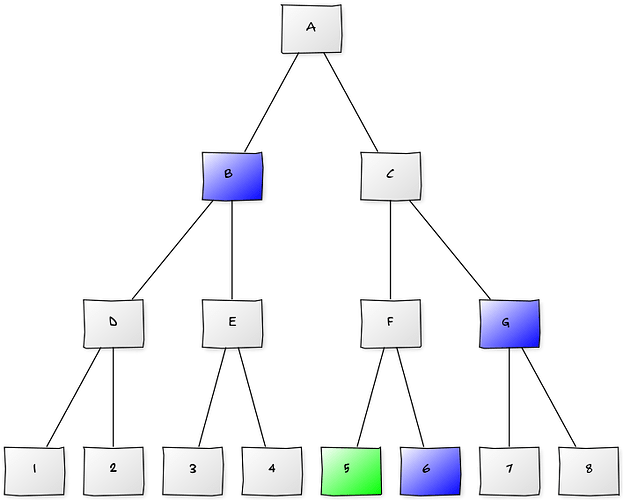
First we will build a binary tree, with all leafs representing the coins. Every coin has one corresponding node in every level of the tree, such that all coins except the given coin are below one of the corresponding nodes. See figure below, where the blue nodes are the corresponding nodes of the green coin.
For every corresponding node-coin combination we have a value in a lookup table L = g^{\prod\limits_{k \neq i, k \notin B} q_k} where i is the coin and B is the set of coin numbers below the corresponding node.
We will first initialize the witness values in every node of the tree with the value 1. Then, for every transaction we will raise the value from the lookup table of the corresponding nodes to the power of the hash of the transaction and multiply it with the witness value in the corresponding node.
In the second step we will go down the tree level for level, node for node. The witness value is first raised to the power of all primes of the coins below the left child. This is multiplied to the witness value of the right child. And then the witness value is raised to the power of all primes of the coins below the right child. This is multiplied to the witness value of the left child.
When we have reached the bottom of the tree, the witness values of all coins have been calculated.
To include the time dimension, all witnesses have to be raised to the power of all time primes that have past and be multiplied to the previous witness of the coin.
When there are many blocks in the accumulator raising to the power of all time primes can still be a lot of computation. To solve this we could update the lookup value every time it is used by raising it to the power of all past time primes it does not yet include.
Except for the top levels, this algorithm can easily be parallelized. If we want to parallelize the highest levels more, we could choose to skip the higher levels and start at a lower level. In the figure above we could skip B and send the value of spot 5 to node D and E instead. This will also result in less computations when only a small subset of the coins have a transaction.