Post-Pectra Effects on Ethereum: Reorg Rate, Propagation, and Block Size
This analysis was conducted as part of the Pectra Grants Program by the Decipher Research Team.
We would like to thank the ethPandaOps team for providing Xatu-data, an extensive dataset of Ethereum node measurements, and the Ethereum Foundation ESP team for supporting this work through the Pectra grants round.
Our preprocessed dataset and analysis code are openly available .
TL;DR
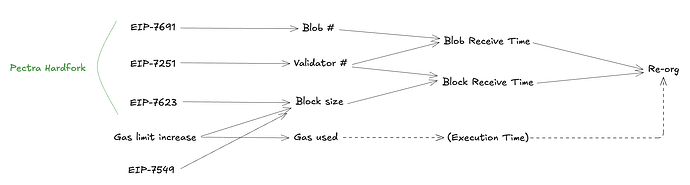
In this post, we empirically analyze the impact of the Pectra upgrade on Ethereum. We focus on how the reorg rate changed, how block and blob propagation times shifted, and how block sizes evolved. We also connect these outcomes to recent protocol changes such as EIP-7623 EIP-7691, and EIP-7549.
Here are key takeaways:
- Reorg rate decreased slightly, from 0.1224% → 0.1121% (~10% lower).
- This reduction aligns with faster propagation times: both blob propagation and block propagation times shifted downward, reducing the fraction of slots with delays near the 4s attestation boundary.
- Large blocks (>400 kB) are more likely to exceed 4s propagation.
- The frequency of such large blocks dropped after Pectra, especially due to EIP-7623.
- The average block size also decreased, mainly driven by EIP-7549, which reduced consensus-layer overhead by aggregating votes.
Contents
- Data collection
- What drives reorgs?
- Re-org rate before vs after Pectra
- Propagation times before vs after Pectra
- blob propagation time
- block propagation time
- Block vs Blob : Which comes faster?
- Block size change
- Big blocks
- Normal blocks
Data Collection
Our analysis uses data from Xatu-data, covering January 1, 2025 to August 27, 2025 (slots #10,738,799 to #12,459,220). The raw data was gathered from the following sources:
- Since beacon_api_eth_v1_events_block_gossip does not provide data before the Pectra hardfork, block propagation times were instead taken from libp2p_gossipsub_beacon_block. The average propagation times from the two sources differ by less than 10 ms, so the values can be regarded as closely aligned.
- Blob propagation times are taken from beacon_api_eth_v1_events_blob_sidecar, and reorg events from beacon_api_eth_v1_events_chain_reorg.
- Validator max effective balance and total validator counts come from canonical_beacon_validators.
- Block size and transaction calldata are collected from canonical_execution_block and canonical_execution_transaction.
What drives reorgs?
Reorgs are an important indicator in measuring the consensus safety. Re-orged slots hurt user experience and add uncertainty for validators.
Several factors may contribute to reorgs. In this analysis, we tested three features:
- blob_prop — the arrival time of the latest blob in a slot.
- block_prop — the time when a block is first seen on the p2p network.
- gas_used — total gas consumed, used here as a proxy for execution time.
We also consider max_prop = max(blob_prop, block_prop), since validators must wait for both the block and all blobs before attesting.
To see how well these features explain reorgs, we fit logistic regression models and report the ROC-AUC scores:
ROC-AUC block_prop: 0.974
ROC-AUC blob_prop: 0.845
ROC-AUC max(block_prop, blob_prop): 0.982
ROC-AUC max(block_prop, blob_prop), gas_used: 0.982
These results show:
- Propagation times are the main driver of reorgs. Both block_prop and blob_prop matter, and their maximum (max_prop) has the strongest predictive power.
- Execution time adds little predictive power. Adding gas_used to the model does not change performance, suggesting execution time has little direct effect on reorgs. Its influence is likely indirect, through its impact on block size and thus propagation.
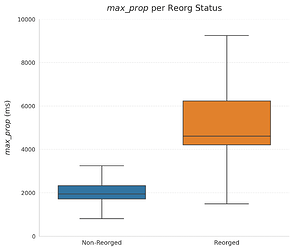
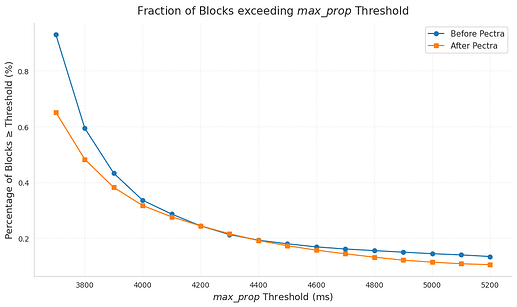
Looking at the distribution of max_prop for reorged vs. non-reorged slots, we find a clear gap. For reorged slots, max_prop is much higher: over 75% of them exceed 4000 ms. This pattern is consistent with default client behavior, where attestations are made around 4 seconds after the slot begins.
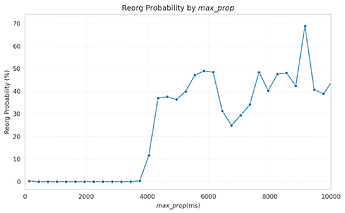
When we bin slots by max_prop and compute the reorg probability in each bin, we see a sharp rise near 3900 ms. In fact, slots with max_prop above 3900 ms show about a 26.7% chance of reorg, highlighting how sensitive reorgs are to propagation delays close to the attestation boundary.
Re-org rate before VS after Pectra
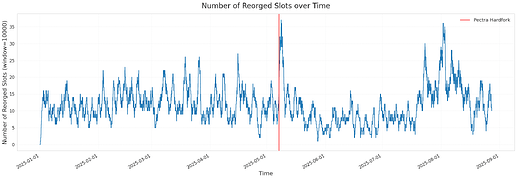
The moving average of re-orged slots shows some fluctuations over time, but the overall reorg rate decreased slightly after Pectra—from 0.1224% to 0.1121%, a reduction of about 10%. This improvement likely relates to changes in propagation times for blocks and blobs. In the next section, we examine how these propagation times shifted after the Pectra hardfork.
| Before | After | |
|---|---|---|
| Total slots | 906,535 | 805,546 |
| Re-orged slots | 1110 | 903 |
| Ratio | 0.1224% | 0.1121% |
Propagation Times before vs after Pectra
| before Pectra | after Pectra | Change | |
|---|---|---|---|
| blob_prop | 1877ms | 1744ms | -133ms (-7%) |
| block_prop | 1887ms | 1832ms | -55ms (-2.9%) |
| max_prop | 2014ms | 1888ms | -126ms (-6.3%) |
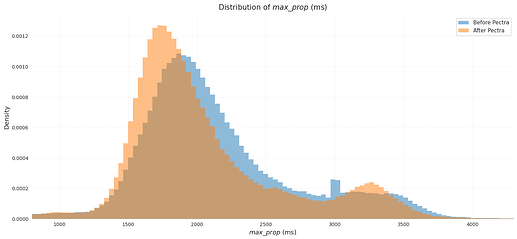
max_prop
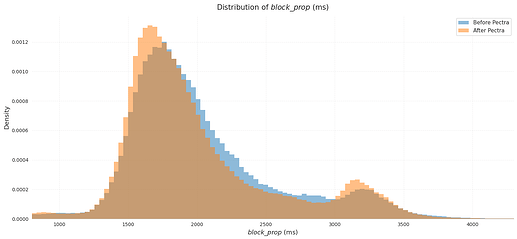
The histogram of max_prop shows a small leftward shift after Pectra. The median decreased from 2014 ms to 1888 ms, a reduction of about 126 ms.
More telling than the median is the share of slots with very high propagation times. Slots exceeding 3800–3900 ms are much more likely to reorg, and this fraction is slightly lower in the post-Pectra period than before.
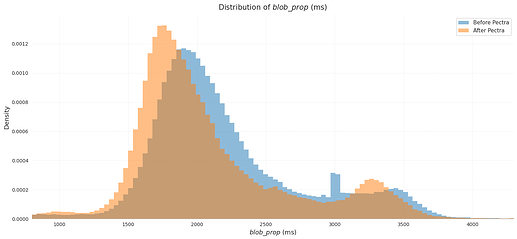
blob_prop
blob_prop, the latest blob propagation time, also decreased noticeably after Pectra: the median dropped from 1877 ms to 1744 ms, a reduction of about 133 ms. This is notable because EIP-7691 raised the maximum blob count per slot from 6 to 9.
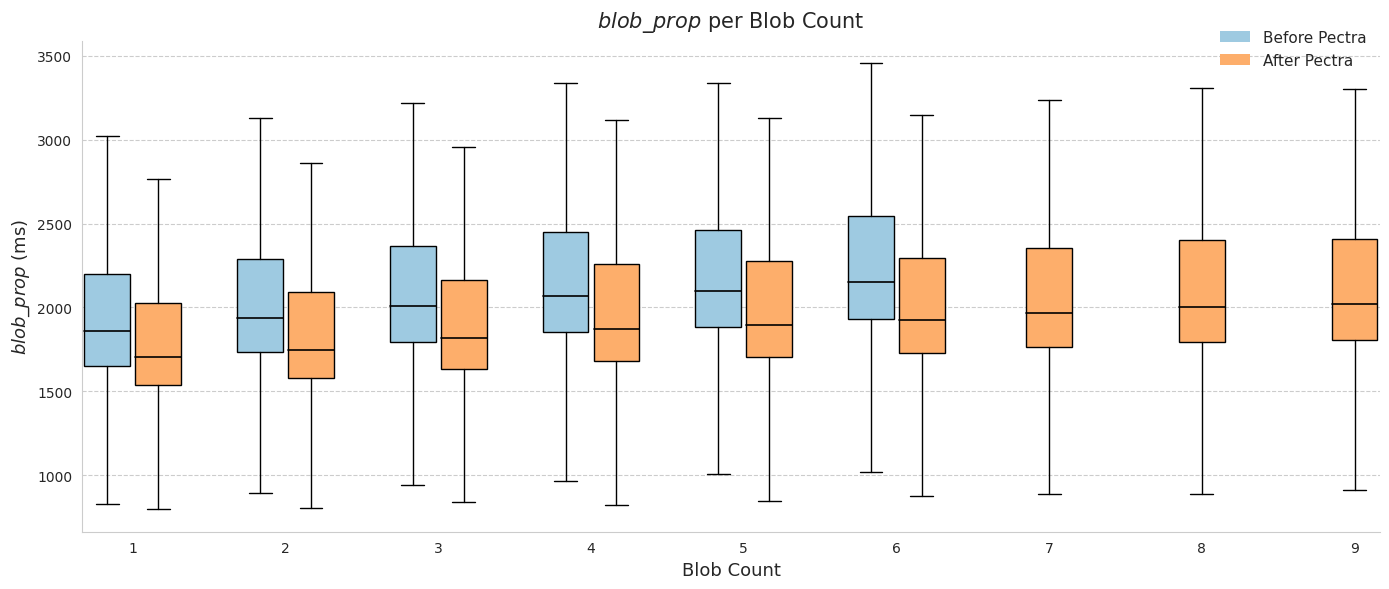
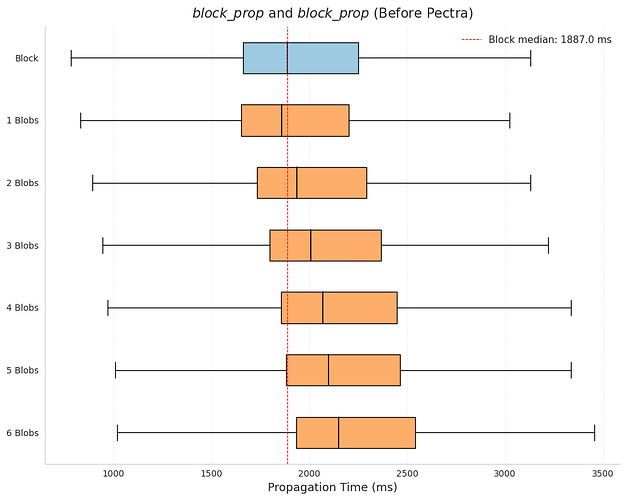
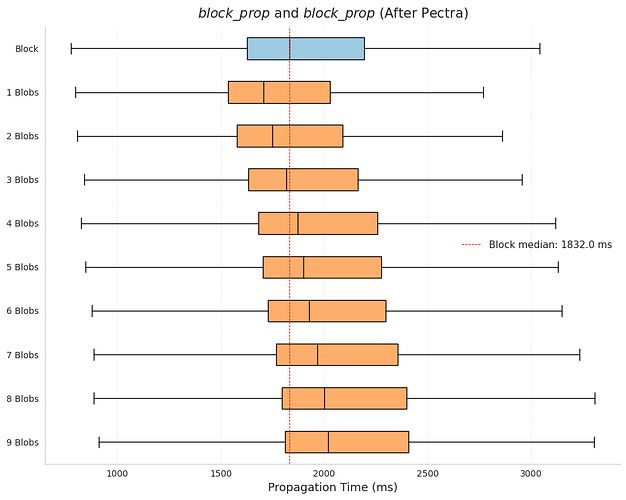
The box plots by blob count show this effect clearly. For every blob count, the median propagation time is lower after Pectra (red) than before (blue). In slots with 6 blobs before Pectra the median was 2151 ms, while in slots with 9 blobs after Pectra it was 2018 ms—despite the higher load, the propagation time was faster.
At the same time, the familiar trend remains: propagation slows as the number of blobs increases. Slots with 5–6 blobs are slower than those with 1–2, and after Pectra this pattern extends into the new 7–9 blob range.
| Blob count | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Before | 1858 | 1937 | 2008 | 2069 | 2097 | 2151 | - | - | - |
| After | 1707 | 1749 | 1816 | 1871 | 1898 | 1927 | 1966 | 2000 | 2018 |
block_prop
Block propagation times also improved after Pectra, though the effect was smaller than for blobs. The median block_prop decreased from 1887 ms to 1832 ms, a reduction of about 55 ms.
Block vs Blob : Which comes faster?
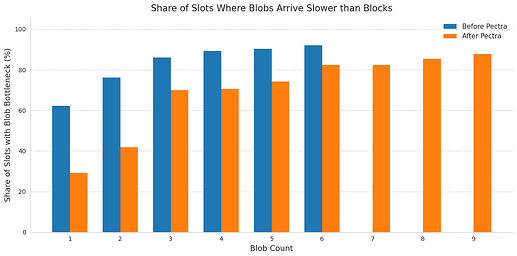
The reduction in max_prop appears to come mainly from faster blob propagation. To check this, we measured how often blobs are the bottleneck when computing max_prop—that is, cases where blob_prop is larger than block_prop.
Before Pectra, blobs were the bottleneck in 85.2% of blob-containing slots. After Pectra, this ratio dropped to 74.9%.
The chart below shows this trend: blob bottlenecks became less common after Pectra. Also, as expected, the chance of blobs being the bottleneck increases with the number of blobs in the slot.
We compared block_prop and blob_prop across slots with different blob counts, before and after Pectra. Before Pectra, once a slot had more than 2 blobs, the median blob_prop was already higher than the block_prop. After Pectra, this threshold shifted upward—blob_prop only exceeded block propagation times once a slot contained more than 4 blobs.
Since block propagation time depends in part on block size, we next examine how recent protocol upgrades have changed block sizes.
Block size change
Recent Ethereum upgrades have affected block size in different ways. EIP-7623 introduced a new gas pricing rule for DA-purpose transactions, encouraging them to move from calldata to blobs. This aims to reduce the worst-case block size. EIP-7549 further reduced block size on the consensus layer by allowing the aggregation of identical votes, which cut down consensus data and lowered the average block size.
At the same time, the maximum block size has also been pushed upward through gas-limit increases: from 30 million to 36 million in January 2025, and then from 36 million to 45 million in July 2025. These changes expanded the ceiling on block size even as other upgrades worked to reduce it.
Big blocks
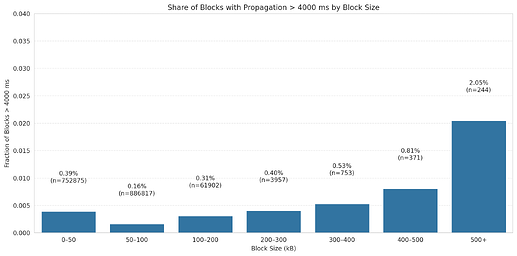
Larger blocks tend to propagate more slowly, which can increase the chance of reorgs. The figure below shows the fraction of blocks with block_prop above 4 seconds, grouped by block size. For blocks smaller than 300 kB—which make up more than 99.5% of all blocks—the fraction with high propagation time is very low and fairly stable. In contrast, very large blocks show a clear penalty. For example, blocks larger than 500 kB have a 2.05% chance of exceeding 4 seconds in propagation.
This shows that while most blocks are small enough to propagate quickly, the rare very large blocks introduce a noticeable delay and higher reorg risk. The reductions in block size brought by EIP-7623 therefore play an important role in limiting the occurrence of these slow-propagating blocks.
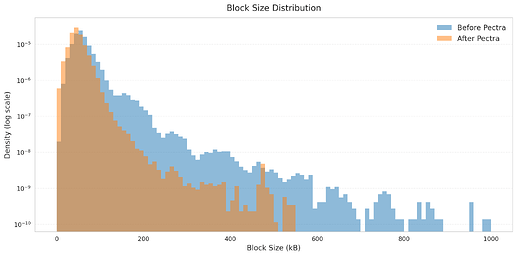
The distribution of block sizes shifted noticeably after Pectra. The figure compares the pre-Pectra period with the post-Pectra period, plotted on a log scale. This shows that EIP-7623 cut down the extreme cases. By limiting the occurrence of very large blocks, it helped reduce the long propagation delays that are most likely to contribute to reorgs.
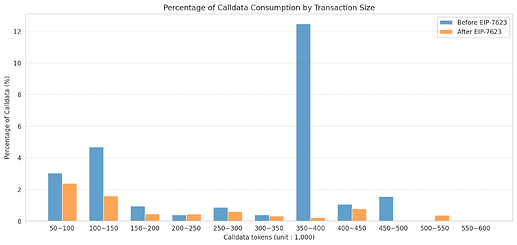
The reduction in the ratio of big blocks can also be explained at the transaction level. The figure shows the percentage of total calldata consumed, grouped by calldata size, before and after EIP-7623.
Before EIP-7623, a large share of calldata consumption came from very big transactions, especially those in the 350–400k token range, which alone accounted for over 12% of all calldata used. After EIP-7623, this heavy concentration nearly disappeared. Other high-calldata ranges (above 100k tokens) also dropped sharply.
This pattern shows that EIP-7623 successfully shifted the data load away from calldata. By cutting down extreme calldata-heavy transactions, it reduced the chance of producing very large blocks, which in turn helps block propagation.
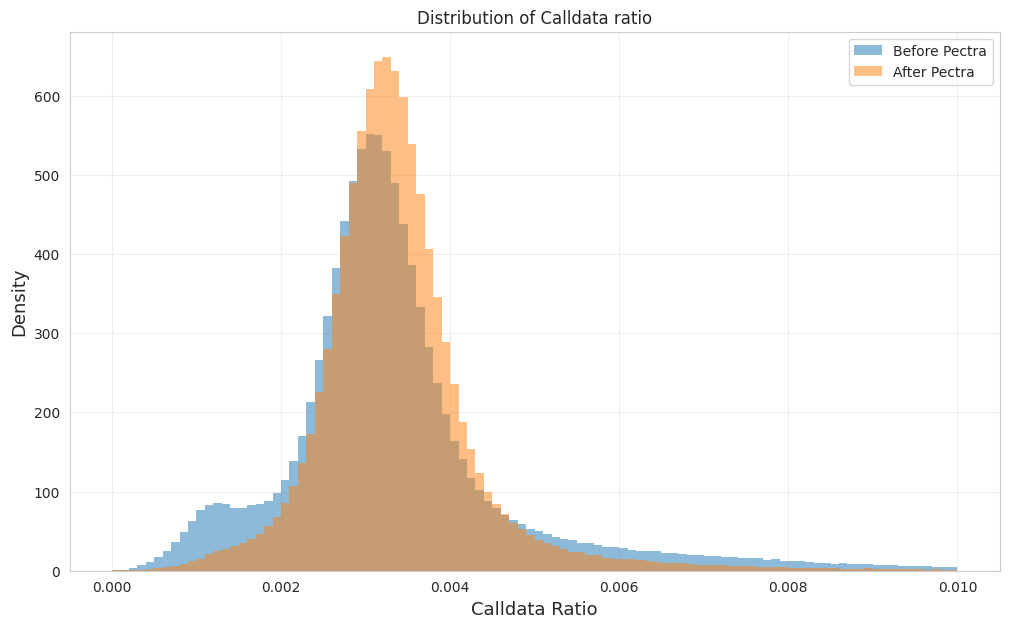
We also analyzed the calldata ratio, defined as the total calldata size in a transaction divided by its gas usage. After EIP-7623, the distribution became more concentrated around the center, with noticeably lower variance. This indicates that extreme calldata-heavy transactions have become less common, making block sizes more stable.
Normal blocks
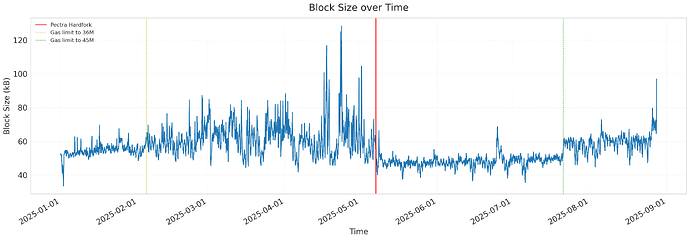
The chart below shows the total block size over time. As the gas limit increased from 30M to 36M, and later from 36M to 45M, average block size rose accordingly. A notable break occurs at the Pectra hardfork: block sizes dropped sharply after the fork, and the fluctuations became visibly smaller as well.
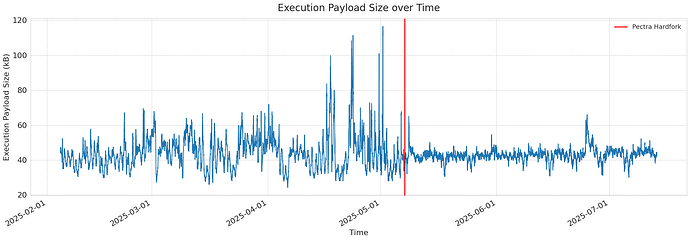
To make a fair comparison, we focus on the period when the maximum gas limit was fixed at 36M. In this window, the execution payload size stayed almost the same, showing only a 2.9% reduction. By contrast, the variance of execution payload size fell sharply from 31,735 byte to 18,637 byte, an effect largely attributable to EIP-7623.
| before (byte) | after (byte) | Change | |
|---|---|---|---|
| execution payload size | 44136 | 42839 | -1297(-2.9%) |
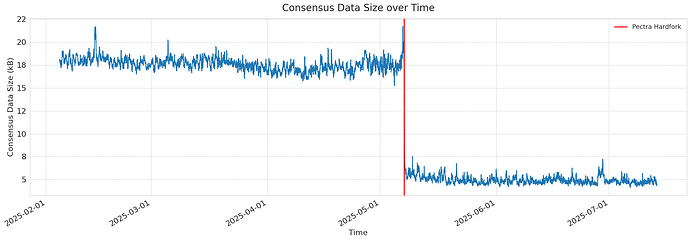
| consensus size | 17603 | 4965 | -12638(-71.8%) |
| total block size | 61739 | 47805 | -13934(-22.6%) |
Consensus data size, defined as the difference between total block size and execution payload size, fell by more than 12KB, which corresponds to a 70% reduction. This points to EIP-7549 as the main driver of block size reduction, with EIP-7623 contributing primarily by stabilizing execution payload variability.
Conclusion and Future works
The Pectra hardfork, together with recent gas limit increases, has changed several aspects of Ethereum’s performance. Scalability improved for both blocks and blobs, with smaller average block sizes, fewer extreme outliers, and reduced variance. These changes helped lower propagation delays, and the reorg rate decreased slightly, suggesting that consensus security has not been harmed and may even have improved.
What remains uncertain is the precise cause of the faster propagation. Both block and blob propagation times fell, but it is unclear whether this came from client-level optimizations, network effects, or validator dynamics. EIP-7251 could eventually reduce network load by lowering validator counts, but this effect was not visible during our analysis window. Future work should look deeper into client and network factors, and monitor long-run validator participation under EIP-7251, to better explain the observed improvements.