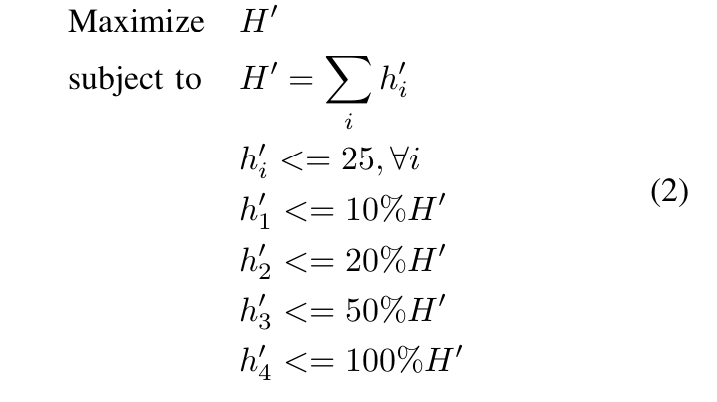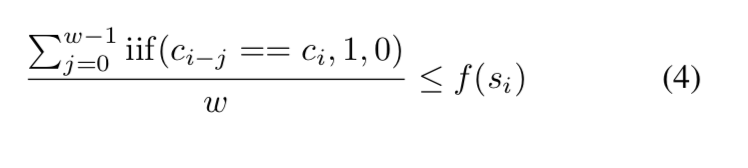Introduction
Currently, the major consensuses in public blockchains are proof of work (PoW) and proof of stake (PoS) and its variants (e.g., dPoS). Since its debut from Satoshi’s infamous white paper, PoW has demonstrated its strong security; however, it is slow and energy inefficient. PoS is more efficient in terms of energy resources; however, it suffers from several security concerns such as nothing at stake, staking grind, and long-range attack. To harvest the benefits of both PoW and PoS, hybrid PoW/PoS such as DASH and Decred are proposed. DASH incentivizes users to set up a masternode by staking 1000 DASH, and allows almost instant payment via InstantSend. However, DASH still suffers from the famous 51% double-spending attack. In Decred, every PoW-mined block must be signed by multiple stakers before appending to the chain, and thus Decred achieves better security (51% attack) when the stakers are decentralized enough.
In this article, we propose a simple hybrid PoW/PoS – proof of staked work (PoSW). The basic idea is that, if a miner wants to contribute its all hash power to the network (suppose p percent of all hash power of the network), the miner must stake the number of tokens that is proportional to p. This means that to perform a double-spending attack, the attacker has to stake some amount of tokens besides 51% of the hash power of the network. In addition, a mining pool will be more costly to run since the owner of the pool must acquire sufficient stake before maximizing the efficiency of all hash power the pool collected.
In the following, we will formulate the consensus model, propose a simple implementation of PoSW, and discuss some results from Monte-Carlo simulation.
Consensus Model
Suppose the hash power of a miner in the network is h_i (in terms of hash per second), the PoSW is formulated as the following problem:
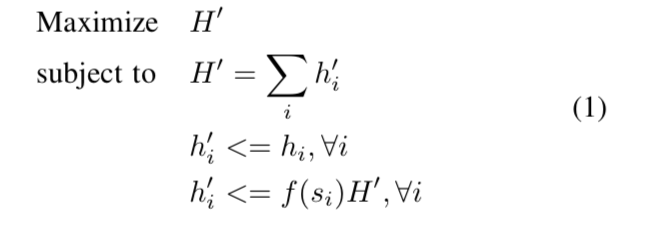
where h’_i is the effective hash power of ith miner, H’ is the total effective hash power of the network, s_i is the stake of the miner, and f(s_i) is the maximum percentage of the hash power the miner i could contribute to the network, namely, allowance. Function f(x) should have the following two properties:
- f(x) is a non-decreasing function; and
- f(x) is a super-addtive function, i.e., f(x) + f(y) <= f(x + y). This makes sure that a miner cannot get more allowance by splitting its stake.
A simple example of f(s_i) is min(alpha * s_i / S, 100%), where S is the total circulated tokens, and alpha is a system-wise constant. To simplify the model, we will use this example equation in the rest of the article.
The problem in (1) is a linear programming problem, which can be efficiently solved by LP solvers in polynomial time. To better understand the model, let us put some example numbers into the model and solve the problem: suppose there are four miners with each of them having equal hash power of the network, e.g., 25 H/s, and the percentage stake of each miner is [5%, 10%, 25%, 60%] and alpha = 2, then the PoSW model in (1) becomes:
By solving the problem in (2), we have
h’_1 = 7.14286, h’_2 = 14.2857, h’_3 = 25, h’_4 = 25 and H’ = 71.4286. The percentage of effective hash power contributed to the network by each miner is:
[10%, 20%, 35%, 35%]
From the result, we observe that:
-
Even all of the miners have the same hash power, their effective hash power is bounded by their stake. This encourages the miners with an insufficient stake to acquire more stake to maximize their hash power.
-
The total effective hash power could be lower than the total hash power. This means a miner with sufficient stake may be easier to mine if other miners do not have sufficient stake.
-
A double-spending attack requires 51% of the effective hash power and 1/alpha percent of the stake in order to create a fork mined by the attacker solely.
-
By adjusting alpha, we could tune the system to be more in the favor of miner or staker.
-
It is possible that given a list of hash power and stake, and alpha, the problem does not have a feasible solution. For example, the miner does not have sufficient stake, while the stakers do not want to mine the network. This is similar to the availability problem of staker (validator) in a pure PoS system. However, in this case, the stakers will be incentivized to mine the network because of the low hash power of the network. To further eliminate such case, we may still allow a miner to produce a block but the block must reach much higher difficulty than others (e.g., beta times higher difficulty than other miners with sufficient stake, where beta could be 2, 5, 10).
-
A mining pool in PoSW needs significant more cost compared to PoW. To efficiently mine blocks, depending on the percentage of the effective hash power of the pool, the pool has to acquire the corresponding stakes in the network. In contrast, the running cost of a decent-size mining pool in PoW is almost negligible compared to its hash power.
Implementation
In this section, we illustrate a simple and approximate implementation of PoSW and demonstrate its performance via simulation. First of all, we could estimate the effective hash power percentage of a miner at the block with height i by calculating the number of blocks produced by the miner in a recent window:
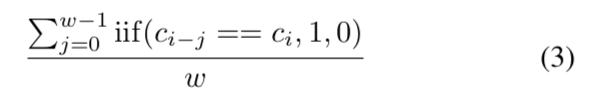
where w is the window size, c_i is the coinbase address of the ith block, and the summation calculates the number of blocks mined by the same miner.
To impose PoSW, the implementation requires that for a block with height i, a valid block produced by a miner must satisfy
Where s_i is the balance of the miner address c_i at block i.
A couple of comments are of interest:
- Assuming the total effective hash power is constant over the window, we could improve the estimation of the percentage of effective hash power of each miner by increasing the window size. We will study the effect of the window size in the simulation.
- To avoid the miner circumvent the allowance by transferring the stake to another address during the window (and thus mine using the new address), the stake (i.e., balance) of the coinbase address will be locked until the window is expired.
Simulation
In this section, we will study the performance of the proposed PoSW implementation via simulation. The simulator accepts the following parameters as input:
- Hash power (in terms of hash per second) of each miner
- Window size
- Maximum blocks could be produced by a miner, derived from their stake
- Number of blocks simulated
To produce each block, the simulator will exclude the miners that do not satisfy equation (4) by checking the number of blocks produced by each miner in the recent window and comparing its allowance and then randomly select the block producer in the rest miners weighted by their hash power. The code of simulation can be found in https://github.com/QuarkChain/pyquarkchain/blob/2a351032dc3ffd85249a3ffff42bc729940350ef/quarkchain/experimental/proof_of_staked_work.py. Unless otherwise specified, the default number of blocks to simulate is 100K
Simulation 1: PoSW with Different Allowances and Equal Hash Power
We simulate the previous example with equal hash power, stake [5%, 10%, 25%, 60%], alpha = 2, and the window size being 128. The allowance list is [10%, 20%, 50%, 100%]. A simulation result of the percentage of actual blocks produced by each miner is:
Miner 1: 9.07%
Miner 2: 18.62%
Miner 3: 36.23%
Miner 4: 36.08%
where we observe that all miners have a close result to the expected result [10%, 20%, 35%, 35%], although miner 0 and miner 1’s percentage is slightly smaller than expected. This is because the window size 128 is small, and as a result, the granularity of the estimate of effective hash power is large. To further study the effect of window size, the following lists the results of different window size:
| Window size | 64 | 128 | 256 | 512 |
|---|---|---|---|---|
| Miner 1 | 8.79 | 9.07 | 9.59 | 9.87 |
| Miner 2 | 17.29 | 18.62 | 19.40 | 19.65 |
| Miner 3 | 36.74 | 36.23 | 35.57 | 35.16 |
| Miner 4 | 37.18 | 36.08 | 35.44 | 35.32 |
where it is clear that by increasing the window size, the percentage of blocks produced by each miner will be closer to the expected one.
If a miner exceeds its allowance and we allow the miner to continue mining with higher difficulty (by a factor of beta), the following table summarizes the percentage of blocks produced with various beta and windows size = 256:
| beta | 2 | 5 | 10 | Inf |
|---|---|---|---|---|
| Miner 1 | 16.03 | 10.26 | 9.79 | 9.59 |
| Miner 2 | 20.28 | 19.61 | 19.50 | 19.40 |
| Miner 3 | 31.91 | 34.84 | 35.26 | 35.57 |
| Miner 4 | 31.78 | 35.29 | 35.45 | 35.44 |
Where when beta = 2, the miner with small allowance will produce much more blocks, while when beta = 5, the percentage of the blocks produced by miners is close to that of beta = Inf.
Simulation 2: PoSW with Different Hash Powers and Equal Allowances
In this subsection, we simulate a network with hash power [100, 200, 400, 800, 1600], equal stake (20%), alpha = 2, and the window size being 256. The allowance list is [40%, 40%, 40%, 40%, 40%]. A simulation result of the percentage of actual blocks produced by each miner is:
Miner 1: 4.01%
Miner 2: 8.09%
Miner 3: 16.22%
Miner 4: 32.51%
Miner 5: 39.18%
where the expected result is [4%, 8%, 16%, 32%, 40%]. Note that, the percentage of the miner with the largest hash power is slightly smaller than the expected value.
The following table further summarizes the percentage of blocks produced with various beta and windows size = 256:
| beta | 2 | 5 | 10 | Inf |
|---|---|---|---|---|
| Miner 1 | 4.04 | 4.12 | 4.03 | 4.01 |
| Miner 2 | 7.97 | 8.09 | 8.08 | 8.09 |
| Miner 3 | 15.85 | 16.15 | 16.34 | 16.22 |
| Miner 4 | 31.86 | 32.23 | 32.33 | 32.51 |
| Miner 5 | 40.28 | 39.31 | 39.22 | 39.18 |
Where in the case, when beta = 2, the percentage of the blocks produced by miners is very close to that of beta = Inf.
Summary
In this article, we introduce proof of staked work (PoSW), where to maximize the hash power that a miner could contribute to the network, a miner has to acquire some stakes proportional to the percentage of the hash power in the network. A linear programming (LP) model is formulated to describe PoSW, and a simple and approximate implementation is proposed. A simulator is created to verify the performance of the proposed implementation and show that the implementation could yield a very close result to the LP model.