Authors and Reviewers: Electron Team - Garvit Goel, Utsav Jain, Parth Mall, Shubham Yadav
Whenever one wants to prove a large amount of compute using zk-proofs (say trillions of constraints), there are practical limits with schemes such as groth16 since the proving time becomes too large. Recursive systems such as plonky2 present a solution here as they can leverage parallelization. However, often this requires splitting a sequential programme across parallel circuits, which can be a highly custom job for each use case. At Electron Labs, we are trying to generalize this, and this article is a first step in that direction. Here, we will consider a very simple but lengthly computation and aim to prove that using recursive circuits.
Let’s get started.
Consider the scenario, where we start with a number i_0 and hash it once to create i_1. Then we hash it again to create i_2 and so on.
i_1 = SHA(i_0)
i_2 = SHA(i_1) = SHA^2(i_0)
Similarly, i_n = SHA^n(i_0), where n signifies the number of times we have hashed the input.
If we want to prove that i_n = SHA^n(i_0) for large n (say a billion), this would not be practical with groth16. Hence we will use plonky2 style recursive setup for the same.
We assume that not only does the verifier have limited computational resources, they have limited data throughput too. Hence, our goal is to design a circuit such that only i_0, i_n, and the zk-proof need to be shared with the verifier, and no intermediary hashes {i_1 … i_{n-1}} need to be shared.
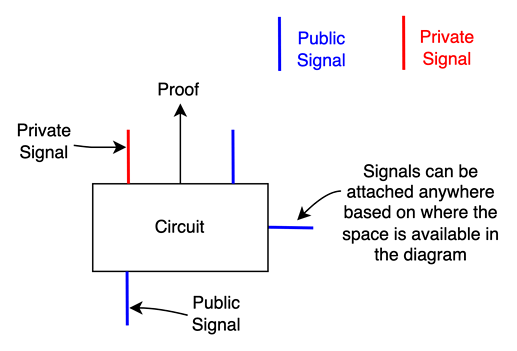
Notation
Let’s get stated with defining the notations first.
Figure1: Notations
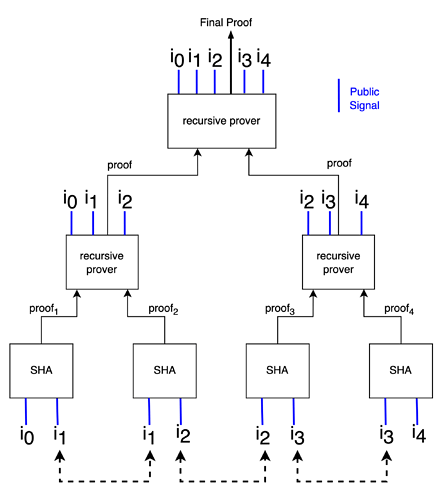
Approach 1: All Hashes as Public Signals
Now, to solve our problem, we can start with a simple construction as follows -
Figure 2: All hashes are public signals
We start with the leaf circuits. Note that the intermediary hash i_1 is common across the first and second leaf circuit. This is true for intermediary hashes i_2 and i_3 as well in the next set of leaf circuits. This is needed to ensure the link across the chain of hashes.
As we move up the tree, the public signals (intermediary hashes) of the leaf circuits become public signals for the circuits that are one level up. As a result, the number of public signals per circuit “build up” as we move up the tree. In the diagram, note that the final node circuit has all the intermediary hashes as public signals, which is a problem.
As we move up the tree, the leaf circuits (SHA) are recursively combined into one proof. While this approach reduces the computational burden of performing a large number of SHA operations by the verifier, we still need to share a large number of hashes, imposing high data throughput requirements on the verifier.
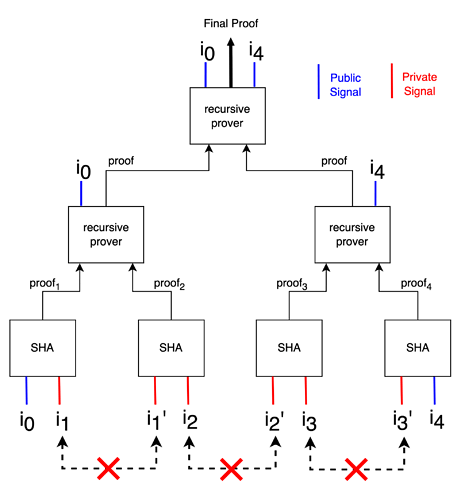
Approach 2: Intermediary Hashes as Private Signals
To solve this problem, we design an alternative circuit, where the intermediary hashes are kept as private signals.
Figure 3: Intermediary Hashes as Private Signals
In this approach, the intermediary hashes {i_1, i_2, i_3} are no longer public signals of the leaf circuits, and hence they don’t need to be passed up to the upper node circuits. This removes the problem of public signal build up as we move up the circuit. But it introduces another problem.
To maintain link across the chain of hashes i.e. i_n = SHA^n(i_0) we must ensure that the output of first circuit i.e. i_1, is the input of the second circuit. This applies for other leaf circuits as well i.e. i_j == i_j’ for j = {1,2,3} (see diagram). But now, since the hashes are private signals, they are not needed to verify the proof. As a result, the prover could provide different i_1 to the first and second circuit (see diagram). This breaks the link between the hashes. As a result, the final circuit only proves that certain numbers were hashed, but not that the output of first hash is the same as the input of the next hash, which is needed to ensure i_n = SHA^n(i_0). Hence this approach does not work.
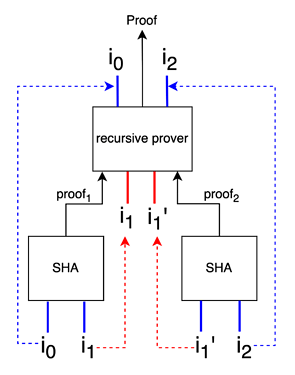
Approach 3: Combination of Public and Private Signals
To solve this problem, we will make the intermediary hashes as public signals for the leaf circuit (to make sure that they part of proof), but make them as private signal in the recursive circuit just above it (see diagram)
Figure 4
Please note that only the intermediary hash i_1 (the one that is common to both circuits) is supplied as private signal to the upper circuit. The initial input i_0 and final hash i_2 are propagated upwards as public signals. When the intermediary hash from both the circuits (i_1 and i_1') reach the upper recursive circuit, we implement a simple equality check inside the recursive circuit i.e. i_1 == i_1’. Now we can rest assured that both the i_1's supplied to each circuit are the same, and hence our recursive circuit proves that indeed i_2 = SHA^2(i_0)
In the diagram, note that i_1 is no longer part of the proof of the upper circuit. It is “proven away”. At leaf level, we supplied i_0, i_1, and i_2, but finally, only i_0 and i_2 are left. We have successfully reduced the data throughput requirements from the verifier without compromising on the information proven.
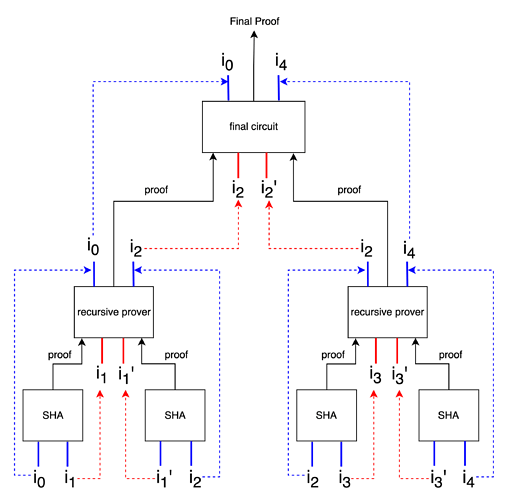
We can now easily span this out for larger N as follows.
Figure 5
The first thing you should note in the above diagram is - the middle level recursive circuits behave as leaf circuits to the final node circuit. Middle level circuits are to the final circuit what leaf circuits are to the middle circuits.
In the previous example, as we moved from leaf circuit to the higher circuit, the intermediary signal i_1 was proven away. Similarly, in this example, as we move from the middle level circuit to the final circuit, the hash i_2 is the intermediary hash that’s gets proven away. Note that i_2 is the common hash for the two middle level circuits. At the final circuit, only i_0 and i_4 are left. i_1, i_2 and i_3 are proven away.
This would apply in the same manner for larger trees. Every time we move to a higher level in the tree, the public signals or intermediary hashes that we want to “get rid of” are turned into private signals for the circuit one level up. As a result, as we successively move up the tree, the intermediary hashes/signals get proven away. The initial input i_0 and final hash i_n, which we want as part of the final proof, can simply be propagated as public signals through the levels. Finally, we are left with the initial input and final hash only, which can then be shared with the verifier along with the proof.
As a result, we can prove to the verifier that i_n = SHA^n(i_0) and share only i_0, i_n and the proof with the verifier.
Further Explanation
Please note that the verification key of each circuit is hard coded in the circuit that is one level up. Let us say the verification key of the leaf circuits is v_{leaf}, then the verification key of the middle circuits v_{middle} is a function of v_{leaf} i.e. v_{middle}= Func(v_{leaf}) . Similarly, the final verification key is v_{final} = Func(v_{middle}) = Func(Func(v_{leaf})). This makes sure that the constraints from leaf level “reach” the final proof. Note that the verification key’s of all circuits at the same level are same.