Questions pertaining to danksharding validation committees

Sharding
1

Hi all,

From this post on two-slot PBS, danksharding is meant to be a two-slot process, meaning (if I’ve understood it correctly) it will take two 8-second slots for the whole build-propose-verify-append process to be completed.

After the intermediate block deadline, we see the remaining ‘N-1 committees’ attest to the block body. My first questions:

  1. Is the committee size here still the same as that intended immediately post-Merge, i.e. 128 validators, or something else?
  2. What is N here? The whole validator set available divided by 128?
  3. These N-1 committees attest to the block body tying up to the block header. But do they also verify for data availability and transaction validity (i.e. check for validity proofs in the case of ZKRs, or raise fraud proofs in the case of ORs)?

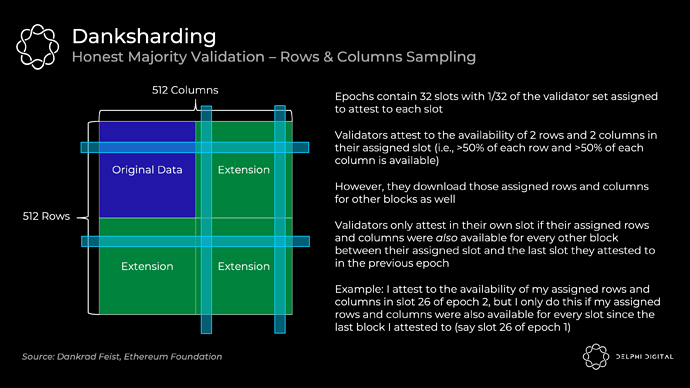
My next questions relate to this popular report, and specifically, this image from it:

12-Danksharding-Honest-Majority
12-Danksharding-Honest-Majority3600×2025 99.6 KB

(Image taken from section titled ‘Danksharding – Honest Majority Validation’.)

My additional questions from the image:

  1. 1/32 of the whole validator set is assigned to attest to the data availability of the block in each slot, as there are 32 slots in an epoch. But with PBS, the block cycle now should take two slots! So is this incorrect? Or should it be something like 1/16 attesting every two slots?
  2. Is ‘1/32 of the validator set’ meant to be the same as the ‘N-1 committees’, and these data availability checks happens at the same time as that process? Or is this data availability verification a separate process with different groups of validators that happens after the ‘N-1 committee’ attestation?
  3. Does the ‘1/32 of the validator set’ also attest to the transaction validity of each block?
  4. Later in the same report it’s stated that it’s intended for the other full nodes (i.e. those not in the validation set) to do their own private data availability sampling. If so, will they also be doing their own transaction validity verifications? This may be trivial for validity proofs, but I expect it may be quite onerous for fraud proofs. How would this work in practice?