TL;DR
Simplified Range Proof. Only 6 ECMUL and 3 ECADD (37K gas) are needed to verify Range Proof of Pedersen Commitment based privacy coin on EVM. The first setup and commitment requires zkSNARKs, but after that, the cost is minimized. For each transaction generation on client side, it does not require ZKP calculations either.
Full paper with the security proof : https://eprint.iacr.org/2025/1811.pdf
Steps:
G,H,B are independent points on a curve.
Onetime setup for each prover (token sender)
- Sample a ← Zq and set the public anchor U = aB.
- Make a Merkle Tree with points on the curve. For each X ∈ {1, . . . , 2 n}, define the leaf payload aXG
- With NIZK on chain, prove the Merkle root of the tree consisting of aXG. (pre-range proof)
Prove (when sending a token)
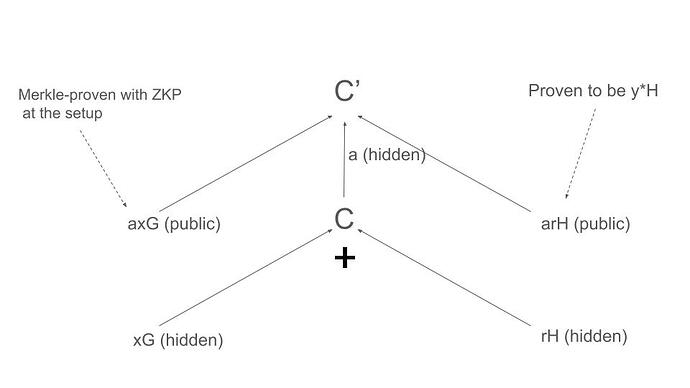
- Make Pedersen Commitment C = xG + rH with token amount x and hiding r. (x, r, xG, and rH should not be exposed)
- Submit C, C’ = aC, axG and its Merkle proof, Chaum-Pedersen DLEQ proof of (U, B) and (C’, C), arH and Schnorr protocol’s proof of (arH, H)
Verify (that C is with x in a range on EVM)
1, Use Chaum-Pedersen DLEQ to check if (U, B) and (C’, C) have a same discrete
2. Use Schnorr protocol or ECDSA to check if the prover can make arH from H.
3. Check the Merkle Proof of axG in the setup tree.
4. Check C’ = axG + arH
## Why Chaum-Pedersen DLEQ and U=aB are needed
If we use Schnorr protocol or ECDSA to check the relationship of (C’, C), a malicious prover can make C’ = yC and C = (bigX)G + rH where y = ax/(bigX). yrH will be verified as well.
How to make the tree smaller
Making a tree with all amount numbers with nonces will be a bit challenging. Making a tree of points by limited random numbers, and multiplying leaves by scalar numbers and adding a point on chain will help a lot, since no one can guess the random numbers from the points on the curve in the tree.