Revisiting Secure DAS in One and Two Dimensions
Authors: Benedikt (@b-wagn), Francesco (@fradamt)
All code is available in a notebook.
I. Introduction
With the Fusaka upgrade, Ethereum will introduce a data availability sampling (DAS) mechanism called PeerDAS. The underlying data units, blobs, are extended horizontally with a Reed-Solomon code and arranged as rows of a matrix. The samples are then columns.
Columns are also the transmission unit on the network, and nothing smaller than a column can currently be exchanged. Due to this, two features are lacking in this initial version of PeerDAS:
- Partial reconstruction: being able to contribute to reconstruction by only reconstructing and re-seeding a part of the data, e.g., only one row (or a few rows) instead of the whole matrix.
- Full mempool compatibility: transactions come with blobs/rows and are often distributed ahead of time in the mempool. However, any single missing blob prevents a node from constructing columns, rendering all of the other mempool blobs useless.
To address these limitations, cell-level messaging has been strongly considered as a candidate for the next iteration of the protocol (see e.g., here). As this is also a key component of a two-dimensional DAS construction, this calls into question whether we should:
- Enhance 1D PeerDAS with cell-level messaging, or
- Transition to a 2D construction.
Or at least whether this transition would be a following iteration. In this post, we compare the efficiency of these two approaches under the assumption that both aim to provide the same level of security while minimizing bandwidth consumption.
Disclaimer: We will entirely ignore the security of the “cryptographic layer”, i.e., the security properties of KZG commitments that are used. This layer has been studied extensively here and here. Our focus are the statistical security properties related to the sampling process, treating the cryptographic layer as idealized.
Background: Data Availability Sampling
Let us begin by abstractly recalling the core idea behind data availability sampling (DAS).
In DAS, a proposer holds a piece of data and wants to distribute it across the network. Clients (which may be full nodes or validators) aim to verify that this data is indeed available without needing to download it in full.
To achieve this, the proposer extends the data using an erasure code. Each client then attempts to download k random symbols of the resulting codeword and checks them against a succinct cryptographic commitment, which all clients download. In the DAS context, these symbols are also referred to as samples or queries. A client accepts the data (e.g., includes the corresponding block in their fork choice) only if all k queries are successfully verified.
The high-level intuition behind the security of DAS (against a potentially malicious proposer) is:
- The cryptographic commitment guarantees that the proposer is committing to a valid codeword (see the notion of code-binding here);
- If enough clients accept, then their collective queries allow reconstruction of the full data, thanks to the properties of the erasure code.
This post focuses on the second point: How is reconstruction actually achieved? How many clients are enough? And how should we set the parameter k?
We begin by addressing the first of these questions, explaining what we mean by partial reconstruction. Then, we shift our focus towards security.
Background: Partial Reconstruction
One of the central questions in DAS is: who can reconstruct the data, and when? Suppose we have an all-powerful “supernode” that can download enough samples from the network to reconstruct the entire data encoded via an erasure code. In such a case, if only a few code symbols are missing—perhaps withheld by a malicious proposer—this supernode can simply recompute the missing pieces and reintroduce them into the network (aka re-seeding). Eventually, these symbols propagate, and all clients accept.
This setup raises the concern of relying on such powerful supernodes, which may be a centralization factor. In fact, even if we use an erasure code with the minimal reconstruction threshold, a so-called MDS code such as Reed-Solomon, the supernode needs to download as much samples as the full original data before it can reconstruct.
This is where the concept of partial reconstruction enters the stage. We say that a code allows for partial reconstruction if small, local portions of the data can be recovered using significantly fewer samples than what’s needed for full reconstruction. Instead of needing a supernode to collect nearly all pieces, multiple smaller nodes can independently reconstruct parts of the data. In this way, partial reconstruction enables distributing the reconstruction task across many participants, reducing the reliance on centralized supernodes.
Besides enhancing the robustness of the network by reducing reliance on more powerful nodes, distributing the CPU load of reconstruction and the bandwidth load of re-seeding the reconstructed data can also be seen as a performance improvement. Currently, reconstruction is unlikely to help the data propagate in the critical path, which one might expect to be another benefit of employing erasure coding, because it takes ~100ms to reconstruct a single blob, with all proofs. By distributing this load across many nodes, each only responsible for one or a few blobs, the erasure coding can be useful for more than security guarantees.
Background: Subset Soundness
In this post, we want to compare different encoding schemes (1D vs 2D) with respect to their efficiency, under the assumption that they all achieve the same level of security. To make this comparison meaningful, we first need a clear understanding of what “security” entails in the DAS context.
The security notion we consider is known as subset soundness and considers an adaptive adversary. This notion is formally introduced as Definition 2 in the Foundations of DAS Paper, and it also underpins the security rationale of PeerDAS.
Intuitively, subset soundness models a powerful adversary who observes the queries made by a large set of n clients/nodes. The adversary can then adaptively decide which symbols to reveal and which to withhold, effectively crafting the view each node sees. The adversary also selects a fraction of the nodes — say, \epsilon n \leq n for some fixed \epsilon > 0 — and aims to fool them into believing that the data is fully available. Notably, this choice can depend on the queries that the nodes made. We then consider the probability p that the adversary wins this game, i.e., that
- the \epsilon n nodes all accept, and
- the data is not fully available; that is: one cannot reconstruct it from their queries.
For our purposes, we want p to be at most 2^{-30} (for any adversary). Below, we will set the number of queries k per node depending on n, \epsilon, and the encoding scheme, such that p \leq 2^{-30} is guaranteed.
Impact and Choice of \epsilon:
The security notion described above is parameterized by \epsilon \in (0, 1], which models the fraction of nodes the adversary attempts to fool. From the formal definition and a simple cryptographic reduction, it follows that subset soundness for a given \epsilon (with fixed n) implies subset soundness for any larger \epsilon' \geq \epsilon. In other words: if an adversary cannot fool an \epsilon-fraction of nodes, then it certainly cannot fool a larger fraction \epsilon'.But how does this relate to the overall consensus protocol? Suppose we know that an adversary cannot fool more than an \epsilon-fraction of nodes. Each fooled node effectively behaves as an additional malicious node in the consensus process. Thus, when data availability sampling is used, the adversary gains up to an extra \epsilon fraction of apparent malicious nodes.
For example, if consensus without DAS tolerates up to <{1}/{3} malicious nodes, then with DAS in place, the system can now tolerate only up to <{1}/{3} - \epsilon malicious nodes.
Therefore, in practice, we must choose \epsilon to be small, say, \epsilon = 1\%, to ensure the adversary’s influence remains negligible.
II. PeerDAS - the 1D Construction
In this section, we explain how PeerDAS works, which will be included in the Fusaka upgrade. We also explain how cell-level messaging enables partial reconstruction.
How it works
We describe how to encode data and how clients make their queries, ignoring everything related to the “cryptographic layer”, e.g., commitments and openings.
A blob is a set of m cells, where each cell holds f field elements. In the current parameter settings of PeerDAS, we have f = 64 field elements per cell, and m = 64 cells per blob. To consider various cell sizes, we let fm = 4096 be constant (i.e., fix the data size), and vary f \in \{64,32,16,8\}, setting m = 4096 / f.
To encode a single blob, one extends the blob using a Reed-Solomon code of rate 1/2, resulting in 2m cells, or equivalently, 2fm = 8192 field elements. In PeerDAS, we apply this encoding process to b blobs independently and view the extended blobs as rows in a b \times 2m matrix of cells.
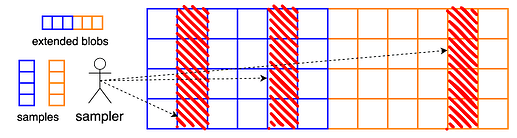
Clients now query entire columns of this matrix, i.e., they attempt to download b cells at once. This means that the “symbols” or our erasure code are columns of the extended blob matrix. From any m of these columns, one can reconstruct the entire matrix and therefore the data.
The concrete networking infrastructure supporting the sampling functionality are GossipSub topics for columns, i.e., sub-networks where only nodes interested in a specific sample (= column) participate.
Partial reconstruction
As anticipated, the current PeerDAS design does not support partial reconstruction. However, even such a one-dimensional encoding can in principle support this feature, when applied independently to many blobs, as it is in PeerDAS. In fact, by working with vertical units smaller than columns, such as cells, it is certainly possible to reconstruct only parts of the full matrix, for example individual rows or groups of rows. This presents two challenges:
- Partial re-seeding: when a node reconstruct a single row, it does not reconstruct any full sample (column), but it still needs to be able to contribute the reconstructed data back to the network.
- Obtaining enough cells to reconstruct: when only sampling columns, ability to reconstruct is all or nothing, i.e., either a node obtains enough columns to reconstruct the whole matrix, or cannot reconstruct any part of it. In other words, only supernodes can participate in reconstruction. We would like nodes to be able to do so while still only downloading a fraction of the whole data.
There are well known ways to approach them, which together give us partial reconstruction:
- Cell-level messaging: enable nodes to exchange cells rather than full columns, so that a node that reconstructs a row can re-seed it cell-by-cell, at least in the column topics that they participate in.
- Row topics: have nodes also attempt to download some rows, by participating in row topics, also equipped with cell-level messaging. Crucially, this is not sampling, and there are no security implications to how many rows are obtained, so even participating in a single row topic suffices. In fact, sampling rows is pointless in a 1D construction, since there is no vertical redundancy. The purpose of a row topic is only that cells from column topics can flow into it and enable row-wise reconstruction, without any supernode. The reconstructed cells can then flow from the row topic into all of the column topics, again without any single node needing to participate in all of them.
Note: the lack of vertical redundancy means that we need every row topic to successfully perform its reconstruction duties. If even a single row topic fails to do so (for example because of a network-level attack limited to the topic), the whole reconstruction cannot complete.
Number of samples
Let us now determine the number of samples k per client for PeerDAS. As discussed above, we want to choose k such that the probability p that an adversary breaks subset soundness is at most 2^{-30}.
The security of PeerDAS has been analyzed extensively here and here. The latter work builds on the security framework from here, and a concrete bound for subset soundness can be derived by combining Lemma 1 and Lemma 3 here. Ultimately, all of this yields the same bound for subset soundness, namely:
p \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot (\frac{m-1}{2m})^{kn\epsilon} \leq \binom{n}{n\epsilon}\cdot \binom{2m}{m-1} \cdot 2^{-kn\epsilon}.
Intuitively, the first binomial accounts for the ability of the adversary to freely and adaptively pick n\epsilon nodes to fool, the second binomial accounts for the adversary choosing m-1 symbols to make available to these nodes, and the final term is the probability that all of their samples end up in this available portion of the encoding.
If we want that p \leq 2^{-30} and n,m,\epsilon are given, we need to set
k \geq \frac{1}{n\epsilon} \left( \log_2 \binom{n}{n\epsilon} + \log_2 \binom{2m}{m-1} + 30 \right).
Here is the code for computing k:
from math import comb, log2, ceil # used later
from tabulate import tabulate # used later
import numpy as np # used later
import matplotlib.pyplot as plt # used later
def min_samples_per_node(n: int, m: int, r: int = 2, eps: float = 0.01):
"""
Finds the smallest integer k such that k samples per node
achieve security of 30 bits for the 1D construction.
Inputs:
n: total number of nodes
m: number of symbols in original data
r: inverse coding rate (total symbols = r*m), default=2
eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01
Returns:
Smallest integer k satisfying the bound
"""
neps = int(n * eps)
binom_n = comb(n, neps)
binom_m = comb(m*r, m-1)
log2_binom = log2(binom_n) + log2(binom_m)
k = -(log2_binom + 30)/(n*eps*log2(1/r))
return ceil(k)
III. The 2D Construction
An alternative to PeerDAS is the two-dimensional construction, which has already been discussed (here and here and here). This construction is based on a tensor code of the Reed-Solomon code, and has been analyzed here, Section 8. It supports a natural form of partial reconstrution.
How it works
We can think of PeerDAS as extending a b \times m matrix (b blobs with m cells per blob) horizontally into a b \times 2m matrix of cells. Equivalently, this is a b \times 2mf matrix of field elements, where each cell contains f field elements. Since the extension occurs only along the horizontal axis, PeerDAS is referred to as a one-dimensional construction.
In the two-dimensional construction, we proceed as follows: starting from the b \times 2mf matrix that is derived as in PeerDAS, we then extend each column vertically using another Reed–Solomon code of rate 1/2. This results in a final matrix of size 2b \times 2mf, or equivalently, a 2b \times 2m matrix of cells.
A key distinction from PeerDAS is that in the two-dimensional construction, clients sample individual cells, not entire columns. That is, a symbol of the code is a single cell, not a full column.
Partial reconstruction
Reconstruction in the two-dimensional construction is naturally a process that involves several sub-processes:
- As soon as at least m cells are available within the same row, that row can be fully reconstructed.
- Similarly, as soon as at least b cells are available within the same column, that column can be reconstructed.
This locality implies that there is no need for a central supernode to reconstruct the entire dataset. Instead, it suffices to have enough nodes that can independently reconstruct specific rows or columns, achieving the same goal in a decentralized manner.
Number of samples
Again, we want to determine the number of samples k per client to achieve a security of the form p \leq 2^{-30}. For that, we need an upper bound for p for the two-dimensional construction.
Using the tools from the Foundations of DAS paper, we can obtain the bound
p \leq \binom{n}{n\epsilon}\cdot \binom{4mb}{4mb - (b+1)(m+1)} \cdot (\frac{4mb - (b+1)(m+1)}{4mb})^{kn\epsilon} = \binom{n}{n\epsilon}\cdot \binom{4mb}{(b+1)(m+1)} \cdot (1-\frac{(b+1)(m+1)}{4mb})^{kn\epsilon}.
To understand this bound intuitively, the reader may convince herself that the maximum amount of cells that can be available such that the 2b \times 2m matrix cannot be reconstructed is about 3/4 of the cells (precisely: 4mb - (b+1)(m+1)). Then, one can follow the same intuitive reasoning as in the one-dimensional construction.
Derivation of the bound:
For the interested reader, we explain the detailed derivation of the bound: first, in the language of the paper, we consider here a tensor code of two codes (see Section 5.2): one with code length 2m and reception efficiency m and one with code length 2b and reception efficiency b. Lemma 26 in the paper shows that the reception efficiency of the tensor code is then t^\otimes = 4mb - (b+1)(m+1) + 1: this means that any set of cells of size \geq t^\otimes is sufficient to reconstruct the matrix. Once the reception efficiency is known, the paper gives the result by combining Lemma 1, Lemma 9, and Lemma 3 with \Delta = t^\otimes-1.
Again, we rearrange to find an expression for k:
k \geq -\frac{ \log_2 \binom{n}{n\epsilon} + \log_2 \binom{4mb}{w} + 30 }{ n\epsilon \cdot \log_2 \left(1 - \frac{w}{4mb} \right) }, where w = (b+1)(m+1).
Here is the code for computing k:
def min_samples_per_node_2d(n: int, m: int, b: int, r: int = 2, eps: float = 0.01):
"""
Finds the smallest integer k such that k samples per node
achieve security of 30 bits for the 2D construction.
Inputs:
n: total number of nodes
m: number of symbols in one blob (before extension)
b: number of blobs (before extension)
r: inverse coding rate (total symbols = r*m*r*b), default=2
eps: fraction of nodes to be fooled (0 < eps <= 1), default=0.01
Returns:
Smallest integer k satisfying the bound
"""
neps = int(n * eps)
binom_n = comb(n, neps)
total = r**2 * m * b
withheld = (m+1) * (b+1)
binom_m = comb(total, withheld)
log2_binom = log2(binom_n) + log2(binom_m)
k = -(log2_binom + 30)/(n*eps*log2(1 - withheld/total))
return ceil(k)
IV. Results
We now consider various settings of n and \epsilon, comparing the 1D and 2D solutions, both with different cell sizes. Some of these configurations are primarily instructive, aimed at illustrating the bounds and highlighting key differences between the schemes. Others reflect realistic scenarios for Ethereum, which are ultimately the most relevant. For each configuration, we present the corresponding code and resulting graph, accompanied by an explanation of the observed behavior. In the graphs, we show the fraction of total data per node on the y-axis, and we vary \epsilon or n on the x-axis.
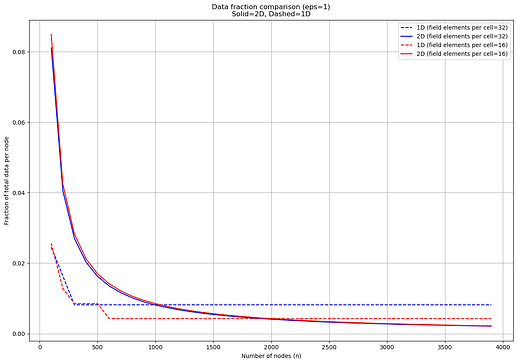
Setting 1: Large \epsilon, Varying n
The first setting that we consider is \epsilon = 1 and varying n. That is, the adversary wants to fool all nodes. In the bounds, this means that the \binom{n}{n\epsilon} terms disappear. This setting will be instructive to understand the behavior of the bounds.
Here is the code to generate the plot:
# General parameters
blob_count = 128
field_elements_per_blob = 4096
bytes_per_field_element = 32
# Parameters for comparison
eps = 1
n_range = np.arange(100, 2000, 100)
field_elements_per_cell_range = [32, 16]
plt.figure(figsize=(15, 10))
colors = ['blue', 'red']
linestyles = ['-', '--']
for i, fes_per_cell in enumerate(field_elements_per_cell_range):
cells_per_blob = field_elements_per_blob // fes_per_cell
# overhead per query: unit is cells, need to download 1 cell and KZG opening (1 group element)
overhead_per_query = 1 + (48 / bytes_per_field_element / fes_per_cell)
# Calculate plot for one dimensional
k_values = [min_samples_per_node(n=n, m=cells_per_blob, eps=eps) for n in n_range]
fraction = [(k * overhead_per_query * blob_count) / (cells_per_blob * blob_count) for k in k_values]
plt.plot(n_range, fraction,
color=colors[i], linestyle=linestyles[1],
label=f'1D (field elements per cell={fes_per_cell})')
# Calculate plot for two dimensional
k_values = [min_samples_per_node_2d(n=n, m=cells_per_blob, b=blob_count, eps=eps) for n in n_range]
fraction = [(k * overhead_per_query) / (cells_per_blob * blob_count) for k in k_values]
plt.plot(n_range, fraction,
color=colors[i], linestyle=linestyles[0],
label=f'2D (field elements per cell={fes_per_cell})')
plt.grid(True)
plt.xlabel('Number of nodes (n)')
plt.ylabel('Fraction of total data per node')
plt.title(f'Data fraction comparison (eps={eps})\nSolid=2D, Dashed=1D')
plt.legend()
plt.show()
The result looks like this:
For \epsilon = 1, the 1D bound simplifies to k \geq \frac{1}{n}\left(\log_2 \binom{2m}{m-1} + 30 \right), whereas the 2D bound to k \geq -\frac{ \log_2 \binom{4mb}{w} + 30 }{ n\cdot \log_2 \left(1 - \frac{w}{4mb} \right) }. Keeping everything but n constant, we have in both cases something of the form \frac{c}{n} . However, in the above plot we only see that for the 2D case. To understand why, let’s look more closely at the bounds.
The binomial coefficient in the 1D bound approximates to \frac{2^{2m}}{\sqrt{m\pi}}, the bottom part of which is close to negligible once the log is applied (~5 for the values of m we are considering). That gives k \ge \frac{2m + 30}{n}. But k is always at least \ge 1 (nodes always sample at least something), and it is going to be 1 for any n \ge 2m + 30, so already for n = 286 resp. n = 542 for m = 128 resp. m = 256. Beyond that, the minimum sample size just does not allow nodes to get an even smaller fraction of the data, i.e., we have hit the maximum possible efficiency of the protocol.
Another way of looking at it: \frac{k}{m} \approx \max(\frac{1}{m}, \frac{2}{n}) is the fraction of the original data per node. Maximum efficiency is \frac{1}{m} since you can’t go below k=1, while in the normal regime it’s \frac{2}{n} since n nodes should collectively get $\approx 2$x the original data to ensure reconstruction.
For the 2D bound, let’s first substitute w \approx mb for simplicity, giving us k \geq -\frac{
\log_2 \binom{4mb}{mb} + 30
}{
n\cdot \log_2(0.75)
}. We can approximate the binomial as:
\binom{4mb}{mb} \approx \binom{4mb}{2mb} e^{-\frac{(4mb - 2mb)^2}{8mb}} \approx \frac{2^{4mb}}{\sqrt{2mb\pi}} e^{-mb/2}. Ignoring the denominator again, we get:
k \ge -\frac{4mb - (\log_2{e})\cdot\frac{mb}{2}+ 30}{n \log_2(0.75)} \approx -\frac{3.3mb + 30}{n \log_2(0.75)} \approx \frac{8mb}{n}.
The key difference with the 1D case is that we have the much larger term \approx 8mb in the numerator, so n can grow much larger before hitting k = 1. Intuitively, we just have many more smaller samples in the 2D case (2b times as many), so we can keep lowering the number of samples per node for much longer. Even when we finally hit the maximum efficiency case of k=1, this is b times less data per node than in the maximum efficiency case for 1D sampling, since a 2D sample is b times smaller than the equivalent 1D sample.
Another way of looking at it: \frac{k}{mb} \approx \max(\frac{1}{mb}, \frac{8}{n}) is the fraction of the original data per node. Maximum efficiency is \frac{1}{mb}, while in the normal regime it’s \frac{8}{n}. When both 1D and 2D are in the normal regime (which is only for small n), 2D is ~4x worse, and when both are at maximum efficiency, it’s b times better. The efficiency pleateau for 2D only happens at n \ge 8mb, \approx 131000 for m=b=128.
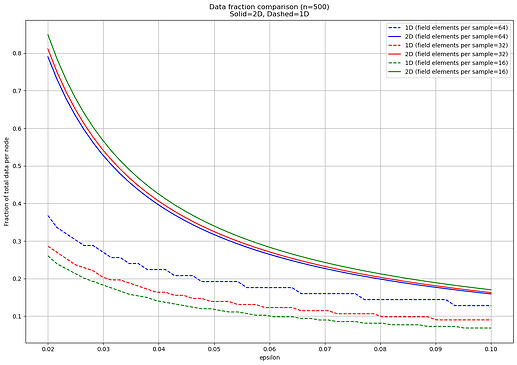
Setting 2: Small n, Varying \epsilon
In the setting before, our explanations have used that n\epsilon is sufficiently large. We will now consider the setting of a small n, namely n = 500 nodes, and vary \epsilon in realistic regimes.
Here is the code:
# General parameters
blob_count = 128
field_elements_per_blob = 4096
bytes_per_field_element = 32
# Parameters for comparison
field_elements_per_cell_range = [64, 32, 16]
eps_range = np.linspace(0.02, 0.1, 50)
n = 500
plt.figure(figsize=(15, 10))
colors = ['blue', 'red', 'green']
linestyles = ['-', '--']
for i, fes_per_cell in enumerate(field_elements_per_cell_range):
cells_per_blob = field_elements_per_blob // fes_per_cell
# overhead per query: unit is cells, need to download 1 cell and KZG opening (1 group element)
overhead_per_query = 1 + (48 / bytes_per_field_element / fes_per_cell)
# Calculate for min_samples (1D)
k_values = [min_samples_per_node(n=n, m=cells_per_blob, eps=eps) for eps in eps_range]
fraction = [(k * overhead_per_query * blob_count) / (cells_per_blob * blob_count) for k in k_values]
plt.plot(eps_range, fraction,
color=colors[i], linestyle=linestyles[1],
label=f'1D (field elements per sample={fes_per_cell})')
# Calculate for min_samples_2d
k_values = [min_samples_per_node_2d(n=n, m=cells_per_blob, b=blob_count, eps=eps) for eps in eps_range]
fraction = [(k * overhead_per_query) / (cells_per_blob * blob_count) for k in k_values]
plt.plot(eps_range, fraction,
color=colors[i], linestyle=linestyles[0],
label=f'2D (field elements per sample={fes_per_cell})')
plt.grid(True)
plt.xlabel('epsilon')
plt.ylabel('Fraction of total data per node')
plt.title(f'Data fraction comparison (n={n})\nSolid=2D, Dashed=1D')
plt.legend()
plt.show()
Here is the result:
With \epsilon < 1, the expressions we get are almost the same as before. For the 1D case, k \ge \frac{2m}{n\epsilon} + \frac{\log_2{\binom{n}{n\epsilon}}}{n \epsilon}, and for the 2D case k \ge \frac{8mb}{n\epsilon} + \frac{\log_2{\binom{n}{n\epsilon}}}{n \epsilon\log_2(0.75)}. The difference is only that we are now not dividing by n but by n\epsilon, as this is now the number of nodes that need to be able to collect enough samples to reconstruct, and that there’s the additional term for \binom{n}{n\epsilon}, accounting for the number of \epsilon-subsets that the adversary can choose to target.
The effect of the former is straightforward: if \epsilon is halved, we need at least twice as many samples to make sure that all \epsilon-subsets of nodes can reconstruct, because for each subset we are playing the same game as before, but with half as many nodes. In the 1D case, for example, we simply need any n\epsilon nodes to collect at least 2x of the data. This is in both cases why we observe the fraction of data per node increasing as \epsilon decreases.
The effect of the latter is more nuanced, and explains why we observe a straightforward inverse proportionality in the 2D case but not in 1D. This is because the effect in the 2D case is negligible whenever n \ll mb, since the second term is then dwarfed by the first, while for 1D this is only the case when \epsilon is either close to 0 or to 1, and \binom{n}{n\epsilon} is far from its maximum value \sim 2^n. Otherwise, the term has a noticeable impact in the setting we’re considering, where n and m are roughly comparable. Due to this, we observe the baseline 4x efficiency gap between 2D and 1D closing as \epsilon increases.
Another observation is that the fraction of data per node \frac{k}{m} appears to be almost independent from m in the 2D case, and larger cell sizes (lower m) do worse, none of which holds in 1D. In both cases, there is some overhead from proofs/KZG openings, which is directly proportional to m (smaller cells, more overhead), and this small overhead is precisely what we observe in the 2D case. In 1D, the dominant factor is again the \binom{n}{n\epsilon} term: while the baseline number of samples \frac{2}{n\epsilon} is independent from m, the former is inversely proportional to m, favoring smaller cells. The 2D scheme has already hit the point of diminishing returns for increasing the number of samples, and only gets proof overhead for doing so further, while the 1D scheme has not.
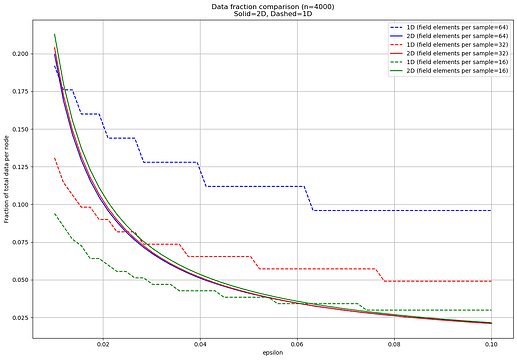
Setting 3: Medium n
Another instructive setting is the case of a medium size n, say, n = 4000. We use the same code as above except for
eps_range = np.linspace(0.01, 0.1, 50)
n = 4000
Here is the result:
Consistent with the previous example, both 1D and 2D become more efficient as \epsilon increases, with 2D gaining on 1D due to the disproportionate effect of the \binom{n}{n\epsilon} term. Moreover, the dependency on cell size is unchanged, with 1D strongly favoring smaller cells and 2D mildly favoring larger ones.
Contrary to the previous example however, 2D is not always strictly worse than 1D, and in fact 2D schemes are better for most of the parameters, and always so for \epsilon > 7\%. This due to the increased effect of the \binom{n}{n\epsilon} term, since we’re considering a higher n.
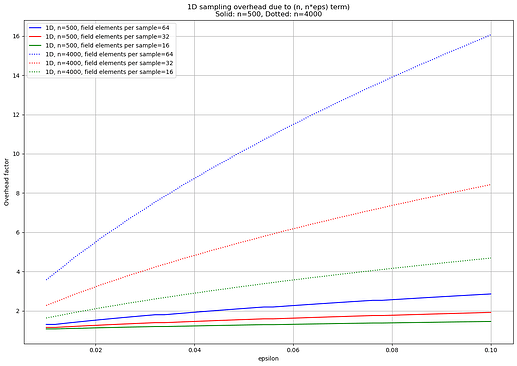
Concretely, the following plot shows the sampling overhead that the 1D scheme incurs due to the \binom{n}{n\epsilon} term, for n=500 and n=4000 (the setting of the two previous plots), where sampling overhead is defined as the ratio \frac{k}{k'} between the (usual) minimum number of samples k and the minimum number of samples k' that would be necessary if we ignored the \binom{n}{n\epsilon} term. In the words of the Foundations Paper, this is subset soundness vs. soundness.
For n=4000, the overhead ranges from ~4x to up to 16x (close to proportional to cell size), at which point nearly all sampling is due to accounting for the adversary’s freedom to choose an \epsilon-subset to target. Moreover, it is always significantly higher than for n=500, which itself incurs a maximum overhead of ~3x.
In short: for larger n, the \binom{n}{n\epsilon} term is more and more relevant for the 1D construction.
Setting 4: The Realistic One
As the final setting, we consider the “realistic setting”, with \epsilon = 0.05 and n = 10000 nodes. In this case, we are interested in the performance of the one-dimensional and the two-dimensional construction, especially as we vary the cell size. To this end, we generate tables using the following code:
n = 10000
eps = 5 / 100
field_elements_per_cell_range = [64, 32, 16, 8, 4]
headers = ["Field elements per sample", "Samples", "Data Per Node (KBs)", "Fraction of data per node"]
# General parameters
blob_count = 128
field_elements_per_blob = 4096
bytes_per_field_element = 32
data = field_elements_per_blob * blob_count * bytes_per_field_element
# 1D sampling
print("")
print("Table for 1D Sampling")
table = []
for fes_per_cell in field_elements_per_cell_range:
cells_per_blob = field_elements_per_blob // fes_per_cell
bytes_per_cell = fes_per_cell * bytes_per_field_element
overhead_per_query = 1 + (48 / bytes_per_field_element / fes_per_cell)
k = min_samples_per_node(n=n, m=cells_per_blob, eps=eps)
row = [
fes_per_cell,
k, # samples needed
k * overhead_per_query * bytes_per_cell * blob_count / 2**10, # data per node (KBs)
k * overhead_per_query * bytes_per_cell * blob_count / data, # fraction of data per node
]
table.append(row)
print(tabulate(table, headers=headers, tablefmt="github"))
# 2D sampling
print("")
print("Table for 2D Sampling")
table = []
for fes_per_cell in field_elements_per_cell_range:
cells_per_blob = field_elements_per_blob // fes_per_cell
bytes_per_cell = fes_per_cell * bytes_per_field_element
overhead_per_query = 1 + (48 / bytes_per_field_element / fes_per_cell)
k = min_samples_per_node_2d(n=n, m=cells_per_blob, b=blob_count, eps=eps)
row = [
fes_per_cell,
k, # samples needed
(k * overhead_per_query) * bytes_per_cell / 2**10, # data per node (KBs)
(k * overhead_per_query) * bytes_per_cell / data, # fraction of data per node
]
table.append(row)
print(tabulate(table, headers=headers, tablefmt="github"))
The resulting tables are:
Table for 1D Sampling
| Field elements per cell | Samples | Data Per Node (KBs) | Fraction of data per node |
|---|---|---|---|
| 64 | 7 | 1834 | 0.111938 |
| 32 | 7 | 938 | 0.057251 |
| 16 | 7 | 490 | 0.0299072 |
| 8 | 8 | 304 | 0.0185547 |
| 4 | 10 | 220 | 0.0134277 |
Table for 2D Sampling
| Field elements per cell | Samples | Data Per Node (KBs) | Fraction of data per node |
|---|---|---|---|
| 64 | 140 | 286.562 | 0.0174904 |
| 32 | 268 | 280.562 | 0.0171242 |
| 16 | 523 | 286.016 | 0.017457 |
| 8 | 1032 | 306.375 | 0.0186996 |
| 4 | 2052 | 352.688 | 0.0215263 |
A few observations:
- Perhaps unexpectedly, the most efficient of all schemes is a 1D scheme, the one with the smallest cell size (4 field elements, corresponding to m = 1024). However, 2D is otherwise more efficient than 1D across the board. This is again due to the sampling overhead from the \binom{n}{n\epsilon} term, which is even larger for n=10000 and very significant for the 1D scheme: it is
[24x, 12.4x, 6.6x, 3.8x, 2.4x]for[64,16,32,16,8,4]field elements per sample, respectively, so that most samples of the 1D scheme are due to this. - The fraction of data required by 1D schemes in this regime is close to proportional to cell size, except for the very small cell sizes of 4 and 8, at which point the proof overhead starts being very significant (37.5% and 18.75%, respectively). The near proportionality is again due to the sampling overhead, which is in all cases much more significant than the proof overhead. Due to this, there’s always a benefit to further decreasing the cell size.
- As has been the case throughout, the performance of the 2D scheme varies very little across the choice of cell sizes, and is in particular almost identical for the range that’s usually considered (
[16, 32, 64]). The only notable exception is the cell size of 4, where the proof overhead is high enough to noticeably increase the fraction of data per node. This leaves the cell size as almost a free parameter, which can be selected based on other considerations, such as the interplay of the network overhead for each message and the efficiencies of fitting a cell into the network MTU, or the CPU overhead of proof computation and verification. - Contrary to 2D, the 1D scheme has a harsh efficiency penalty for choosing bigger cell sizes. Moreover, while the efficiency with cell size 4 and 8 is comparable to 2D, these are very small (128 and 256 bytes) and might be worse in practice (network overhead, computational overhead of proofs). Still, the efficiency penalty for cell sizes 16 and 32 is around 2-3x compared to 2D, which could represent a worthwhile trade-off.
V. Conclusion and Open Questions
In this post, we explored how 1D and 2D encodings and sampling strategies with varying cell sizes compare in terms of efficiency, assuming the same target security level.
In short, for realistic settings with sufficiently large n, the 2D approach or 1D with small cell sizes offer the best sampling properties. Further, cell-level messaging enables partial reconstruction even in the 1D solution.
For the 2D setting, several questions remain regarding the practical implementation of these settings—especially concerning networking:
- Sample distribution: in the current design, data dissemination and sampling coincide, instead of having separate mechanisms for disseminating the data and for sampling. With the high number of samples in 2D schemes, having one GossipSub topic for each sample is unlikely to be the right design, and in fact existing proposals for 2D constructions do this differently, with separation of dissemination and sampling. The analysis of bandwidth efficiency should then also include the dissemination phase, as well as weighing the increased complexity against the advantages of 2D sampling.
- Vertical extension: How should the builder or proposer handle vertical extension? This lies on the critical path, unlike horizontal extension. Is there a streaming algorithm to do this extension as blobs come in?
If these issues cannot be adequately addressed, a 1D approach with smaller cell sizes may remain a viable and simpler alternative.