A discussion about PoS chains at Blockchain Embassy Berlin with Elad Verbin, Vincent Danos, Florian Glatz and others put some attention on this block reward function. While being super trivial, it gives some nice properties that I would like to discuss here.
Introduction:
- A token is used to bond validators into PoS.
- The tokens is also used for economic activity.
- The headers of new blocks are recorded in a contract on Ethereum.
- The token is continuously minted to pay block rewards.
When inflating the token supply to pay validators, value is redistributed from all participants to the validators. How can this redistribution be minimized while still paying enough to keep the chain secure?
Definitions:
r = reward payed for block by minting of tokens.
s = staked supply of tokens.
a = active supply of tokens.
Total supply is active supply + staked supply: t = a + s
n = number of block-rewards payed per year.
i = yearly inflation rate - a value between 0 and 1.
Comparing the sum of minted tokens over a year with total supply gives us the yearly inflation rate:
Using a simple quadratic function of the form y=ax^2+bx+c we can define the inflation rate as follows:
Combining the two definitions we can define reward as follows:
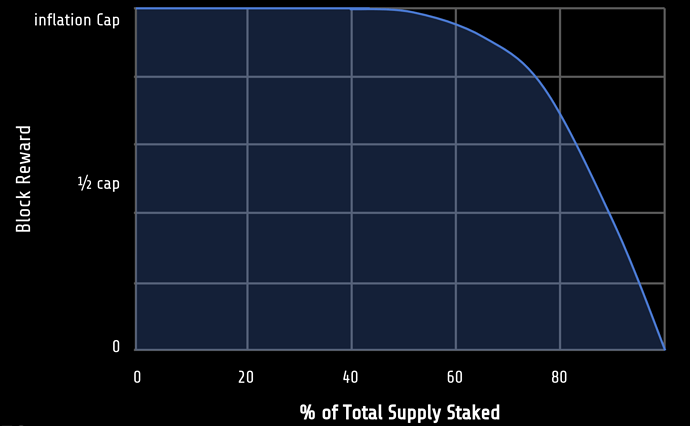
The RISS curve looks like this:
Discussion
Assuming a constant token price, validators are incentivised to stake more tokens when inflation is high. Once the total amount of tokens staked exceeds 50% of supply, the block-rewards start decreasing. Block-rewards continue decreasing until first validators are finding the validation not worth their while and unstake from the chain. Somewhere in the right half of the graph a market equilibrium is found where only the efficient validators can make a profit.
=> Validators enter into competition and market equilibrium is established.
Furthermore we can pick a point on the graph, let’s say 80% and discuss the effects of token price on the validator market.
Token price increases - Validators are making more profits and more tokens are staked to participate in validation. This continues until some validators loose their profit margins and have to unbond. The equilibrium moves to the right. By using a quadratic function, the curve gets ever steeper, preventing that all tokens move into staking - leaving non for the real economy.
Token price decreases - Least effective validators go out of business, and have to unbond, decreasing the supply staked and thus driving up inflation. The equilibrium moves to the left.
Conclusion
Paying the right amount for the security of a chain is hard. Both, the effort of validators as well as the current token price are unknowns. Using the % of staked supply as an indicator of token value allows to create a reflexive rate of token issuance.
 Do you know if there is any more work in this direction and/or if attacks/bugs have been found in the cryptoeconomics of the model?
Do you know if there is any more work in this direction and/or if attacks/bugs have been found in the cryptoeconomics of the model?