I’ve recently been thinking about the Schelling Coin construction, and in particular the P+Episolon attack that Vitalik outlined in a blog post in 2015; the idea of a no-cost bribe is fascinating and frankly, weird. The original post proposes a few mitigations to the attack, but they largely depend on extending the basic Schelling Coin construction, for example by paying voting participants with a secondary token that will (presumably) loose value if the oracle is shown to be compromised, as is done on the UMA protocol. While these mitigations are reasonable, I think the un-extended Schelling Coin may actually be somewhat resistant to attacks. Admittedly, the mitigations proposed are probably better, but the game theory is interesting to dig into nonetheless
Background on P + Epsilon Attacks
If you’re unfamilar with the idea of P+Epsilon attacks on Schelling Coins, the original post explains it very well, otherwise here’s a very brief recap, since in cryptocurrency terms it’s an ancient article:
Schelling Coins are decentralised oracle construction. In the simplest version, oracle participants vote on whether some proposition is True or False. When the votes are tallied, every participant who voted with the majority is given some reward of value P. In the absence of any other guiding process, a participant’s best chance at getting the reward is to assume everyone else will vote honestly, and thus do the same. This is what gives some expectation of honest behaviour from the Oracle.
Payoff matrix under standard conditions:
| You vote false | You vote true
---------------------------------------------------
Others vote false | P | 0
---------------------------------------------------
Others vote true | 0 | P
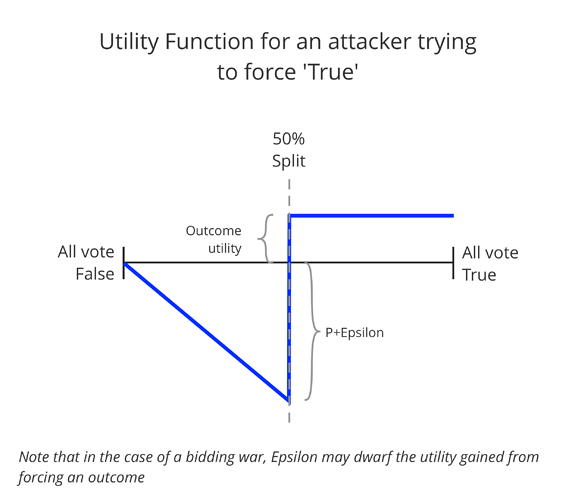
The P+Epsilon Attack is fascinating in that while it involves an attacker bribing participants, a successful execution costs the attacker nothing; If an attacker wants Participants to vote ‘True’ regardless of the actual outcome, they commit to pay out P + Epsilon to all participants who vote True if the majority votes False, but nothing if the majority votes True. Thus the dominant strategy for any participant is to vote True, regardless of what you believe majority will do.
Payoff matrix under a bribe forcing 'true':
| You vote false | You vote true
---------------------------------------------------
Others vote false | P | P + Epsilon
---------------------------------------------------
Others vote true | 0 | P
In the case that the majority votes True, the Attacker both gets the outcome they desire, and doesn’t need to pay anything for it.
The emergence of Bidding Wars
As mentioned, the original post suggests some modifications to the Schelling Coin construction to protect against P+Epsilon, but it’s interesting to consider what protection the pure construction inherently offers.
If the outcome of oracle is worth enough for someone to attack the oracle, then it likely that there exists a counterparty that is equally motivated to have the oracle resolve to the opposite outcome of what the attacker desires. Many oracle-dependant events are zero-sum and so an attacker’s gain is generally someone else’s loss. This could be a loss distributed across multiple counterparties, but we’ll simplify to a single party, because the logic mostly generalises. Contracts that inflate a token supply or similar could behave differently, but that’s a different topic.
So, assuming that there is a counterparty that will incur an equal valued loss to an attacker’s gain, it stands to reason that this counterparty should also attempt to force the outcome they desire, by bribing the oracle with some amount greater than what the attacker is offering. In turn, the original attacker may raise their bribe in attempt to win back the oracle, with the honest party doing the same and so on. In essence, what has resulted is a bidding war. Because the winner incurs no cost, bribed votes are auctioned off in a manner that is largely independent from the actual value resting on the outcome, but rather to whoever has more capital at their disposal to lock into a bribe commitment.
However, it’s important to note that simply having the highest bid does not actually guarantee winning the bribe auction, as participants are perfectly free to vote for whichever outcome they desire. In this sense, the intial attacker is likely at an inherent disadvantage; some voting participants will behave honestly regardless of bribes, perhaps due to moral or other external reasons, or more simply, because they never find out about the bribes that are on offer.
What’s particularly interesting is the payout function for a party bribing oracle. We already know that a successful attack is free, but conversely a failed attack is potentially catastrophic for the attacker. Not only does the attack not have the oracle resolve to the outcome that they desires, the attacker has to pay out P + Epsilon to all participants who voted for the attacker’s desired outcome. The best case scenario for the attacker is that no-one votes for their desired outcome, but at worst the attacker may be obligated to pay bribes to just under 50% of participants (for a binary oracle).
The consequence of this is that a bidding war of Schelling Coin bribes behaves very unlike a regular auction. In regular auctions, such as those for property or political influence, the winning bidder gains whatever is being bid on, but also has to pay the bid price. In a Schelling Coin bribe Auction, the winner has the oracle manipulated to the outcome they desire, but they don’t pay anything - instead that cost goes to the looser, who pays up to ~50% of their loosing bid. So increasing your bid/bribe has very serious consequences, but only if you lose.
The effect of Bidding Wars on Voters
Voters being bribed in a bidding war actually stand to gain the most when they vote for the outcome that they believe will loose. Those who vote for the loosing outcome will receive a payout of P + Epsilon as bribes, while those who vote the winning proposition will only receive a payout of P from the oracle. In a case where a significant bidding war has occurred, this phenomenon is even stronger, as the bribe payouts may dwarf the base payment P.
However, if too many people vote for the outcome with the smaller bribe in anticipation of claiming the Bribe payment, this outcome may actually end up gaining the most votes and winning.
My understanding is that Nash Equilibria can be finicky for group games, but naively it does appear that a Mixed Strategy Nash Equilibrium is able to account for this behaviour. Under MSNE, we would assume that each voter would clue into the risk of the smaller bid winning, and actually vote in a semi-random fashion, picking the Outcome with Higher bribe with a probability of H/(L + H) where H is the value of the Higher Bribe and L is the value of the Lower Bribe.
Intuitively, this somewhat makes sense - if the value of H is much larger than L, the probability of voting for the Higher Bribe approaches 1, as relatively speaking there’s not a lot to gain by picking L, even if it does win. It is notable however that this probability is independent of the base reward value P.
We see two effects from the MSNE on bribing parties. Firstly that there is a non-zero chance that the Higher Bid may end up loosing, even without considering external factors. This increases the coupling between the expected return to an attacker who attempts to force their desired outcome, and the amount they’re willing to bid - there’s little point taking on significant risk over 10,0000ETH in bribes, only to force an outcome worth 1 ETH. Secondly, under conditions where H and L similar in size, the proportion of people voting for each outcome is likely to be close to 50-50, which means that the loosing party is more likely to experience a close to worst-case loss. Note that if we start adding in other factors such as communication and collusion between voters, and prior knowledge regard how other participants are voting, individual behaviour becomes very difficult to predict, so I’m uncertain as to how representative this analysis actually is.
Implications
Collectively, I believe these the viability to bribe an oracle with a P+Epsilon style attack. If your competition comes along with a higher counter-bid, there’s no zero-cost exit strategy, only progressively higher stakes. Conversely, if you know you have significantly more capital available than your hypothetical or realised competition, you may have a very strong motivation to significantly outbid them. The implication of this is that oracle security increases significantly when parties know minimal information about who they might be competing with in a bidding war, as it means would-be attackers can be less certain about whether they would be significantly out-bid by some whale who just happens to have some stake in the outcome. Extending on this, the more parties that have a vested interest in the outcome dictated by an oracle oracle, the more secure it becomes, as a potential attacker has greater uncertainty about whether they may find themselves competing with a whale.
As a closing note, it’s interesting to consider about whether there are any ‘traditional’ analogies to Schelling Coin bribe wars in the non-crypto world. My first impression was that the sheer extent of the ‘Winner Takes All’ effect in the Game Theory here was pretty much unlike anything seen else. This isn’t just a case of the looser receiving, of which there are many examples. I have been able to think of one example - Legal Battles where we can be pretty certain that the looser is going to have to pay the legal fees of the counterparty. I’m sure there are others that I haven’t thought of.