This research was made in collaboration with @AnteroE.
This paper examines the impact of reducing Ethereum slot time on decentralized exchange activity, with a focus on CEX-DEX arbitrage behavior. We develop a trading model where the agent’s DEX transaction is not guaranteed to land, and the agent explicitly accounts for this execution risk when deciding whether to pursue arbitrage opportunities.
We compare agent behavior under Ethereum’s default 12-second slot time environment with a faster regime that offers 1-second subslot execution. The simulations, calibrated to Binance and Uniswap v3 data from July to September 2025, show that faster slot times increase arbitrage transaction count by 535% and trading volume by 203% on average.
The increase in CEX-DEX arbitrage activity under 1-second subslots is driven by the reduction in variance of both successful and failed trade outcomes, increasing the risk-adjusted returns and making CEX-DEX arbitrage more appealing.
TLDR
- For a risk-averse agent with 35% probability of landing the DEX leg, transaction counts increase by 535% when moving from 12-second to 1-second confirmation times. Volume increases by up to 203%.
- The 535% increase in transactions for the risk-averse agent can be decomposed into two channels: 371% from composability and an additional 164 percentage points from de-risking.
- The increase in CEX-DEX arbitrage activity under 1-second subslots is driven by the reduction in variance of both successful and failed trade outcomes, increasing the risk-adjusted returns.
- Unlike the empirical studies that document realized arbitrage outcomes, we model the decision-making problem facing a CEX-DEX arbitrageur under execution uncertainty. This perspective reveals why observed arbitrage activity may substantially understate the latent demand for faster execution: many profitable opportunities are foregone not because they do not exist but because rational agents decline to attempt them given current confirmation times.
- We focus on execution guarantees that can be provided without protocol-level changes, making our analysis applicable to a range of possible mechanism designs, including but not limited to preconfirmations.
- Results are robust across reasonable variations in win probability (\alpha \in \{0.20,0.35,0.50\}) and risk aversion (\lambda \in \{0,0.01,0.03\}).
1. Why do we care about slot time reduction?
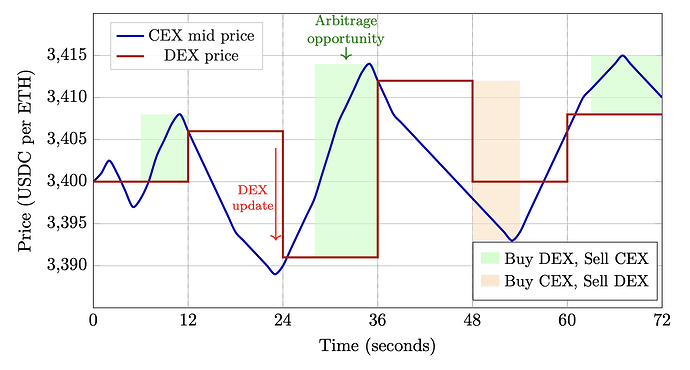
One of the most active sources of DEX volume on Ethereum is arbitrage between centralized and decentralized exchanges. The strategy is simple: when the prices between a CEX (e.g., Binance) and a DEX (e.g., Uniswap) differ, a trader can exploit such an opportunity by simultaneously buying on the cheaper venue and selling on the more expensive one, thus capturing the spread.
However, this strategy is not risk-free: while the CEX leg is executed almost instantaneously, the DEX leg must wait for block inclusion, which is not guaranteed. DEX transactions can fail for multiple reasons, such as insufficient priority fees, another trader capturing the same opportunity, latency, or even the block builder censoring the transaction.
The risk of executing a DEX leg and its relationship to slot times is the focus of our paper. We model a trading agent who knows that their on-chain transaction may fail to land and who incorporates this uncertainty into their entry and exit decisions. The essence of the setup is as follows: the agent faces a known probability \alpha of successfully executing the DEX leg, and if it fails, they must decide how to manage their resulting delta exposure.
The motivation for the paper comes from the interest in understanding how Ethereum slot time reduction would affect the largest portion of DEX volume. We consider a theoretical protocol that operates in 1-second subslots, providing a faster feedback loop for traders compared to Ethereum’s native 12-second slots. The question we address is: how does faster execution change arbitrageurs’ behavior, and what are the downstream effects on DEX activity?
2. Simulation scenarios and data
2.1 Execution regimes
The core objective of the simulation is to quantify how faster execution guarantees change arbitrageur behavior and market outcomes. We run parallel simulations under two execution regimes:
| Regime | Description |
|---|---|
| 12-second slots | DEX transactions can only be executed at Ethereum slot boundaries, occurring every 12 seconds. So, this is the current environment where arbitrageurs face substantial execution windows and corresponding uncertainty. |
| 1-second subslots | DEX transactions can be executed every second through subslot confirmations. This is the improved environment where arbitrageurs receive faster execution guarantees. |
2.2 Environmental configurations
We evaluate agent behavior across multiple environmental configurations to assess the robustness of our findings. Each configuration combines two binary design choices that capture different aspects of market microstructure.
CEX-DEX price reversion: when enabled, subslot DEX prices gradually adjust toward CEX prices between arbitrage events using the regression-based mechanism. This captures informed trading that occurs independently of direct arbitrage.
Noise trading: when enabled, the simulation incorporates random non-arbitrage transactions whose frequency and price impact are sampled from empirical distributions estimated from data. This captures retail flow and other trading activity unrelated to CEX-DEX arbitrage.
2.3 Data
We use data from July to September 2025, including millisecond-level best bid and ask prices from Binance and all swap transactions from Uniswap v3 ETH-USDC pools at the 30 basis point, 5 basis point, and 1 basis point tiers.
2.4 Key parameters
| Parameter | Value | Description |
|---|---|---|
| \alpha | 0.35 | Agent 1’s winning probability |
| \lambda | 0.01 | Risk-aversion coefficient |
| \theta | 0 | Entry threshold |
| Reversion window | 300 seconds | CEX-DEX reversion interval |
| Monte Carlo paths | 16 | Paths at each node |
| Decision wait horizon | 3 seconds | Maximum wait time |
| \bar{k} | 3 | Maximum failed attempts before forced closure |
2.5 Key assumptions
On the execution side: all validators are opted into providing fast execution guarantees; hence, there are no missed slots, and DEX transactions can occur every second; gas fees are zero; agents cannot run out of capital, meaning liquidity constraints do not affect execution, and there are no fees other than DEX pool fees.
On the arbitrage side: every top-of-block arbitrage opportunity is executed; arbitrages are executed with the optimal trade size, moving the DEX price to one pool fee from CEX bid or ask; infinite liquidity exists at the best bid and ask on Binance, and execution on Binance is instant and guaranteed.
On market structure: DEX pools are constant-product (Uniswap v2-style); liquidity is constant except for the increase from swap fees, and all pools start with identical initial liquidity for comparability.
3. Model and results
3.1 Model derivation
DEX Price Interpolation
The simulation framework models the interaction between centralized and decentralized exchange prices over time. Historical DEX prices are readily available and can be used for 12-second slot benchmark simulations. For a faster regime, we need a framework to interpolate these prices for 1-second subslots.
Our framework includes three components. First, we start with a historical price for a current slot. It is also a price for the initial subslot. Next, we derive a price p^{\text{DEX}}(t_i) of the i-th subslot from a price p^{\text{DEX}}(t_{i-1}) of the (i-1)-th subslot. To do this, we apply (1) arbitrage transactions from the previous slot if present, (2) CEX-DEX price reversion to model how DEX prices adjust to off-chain information between arbitrage events, and (3) noise trading to capture non-arbitrage DEX activity.
Noise Trading. We classify historical Uniswap v3 transactions as either arbitrage or noise based on their characteristics. A trade is considered arbitrage if it satisfies all of the following four conditions: (1) it is the first transaction in a block, (2) the pre-trade CEX-DEX price discrepancy exceeds the pool fee, (3) the trade moves the DEX price toward the CEX price, and (4) the post-trade price discrepancy remains equal to or above the pool fee. All other transactions are classified as noise.
CEX-DEX Price Reversion. The idea is to estimate how much the DEX price typically moves in response to a given CEX price change and then use this relationship to revert DEX prices to CEX between arbitrage events. We partition the time axis into semi-open intervals F_k = (\tau_{k-1}, \tau_k] and estimate a linear model within each interval:
For any timestamp t_i within interval F_k, where the CEX price is observed but the DEX price is not yet updated, we predict:
and obtain the reverted DEX price:
Trading Agent Model
CEX-DEX arbitrage exploits price discrepancies between centralized and decentralized exchanges. The core risk is that the two legs of the trade are executed asynchronously. Assuming infinite liquidity and instant and guaranteed execution on Binance, the CEX leg settlement bears no risks, but the DEX leg needs to be included in a block. If the DEX transaction fails to land, the trader is left with unhedged exposure.
We model an agent who explicitly accounts for this risk. The agent has a fixed probability \alpha \in (0,1) of successfully landing the DEX leg of any attempted arbitrage. If the leg fails, the agent must decide how to manage the resulting exposure: close immediately on the CEX, retry the DEX trade in the next slot, or wait for better conditions.
Let p^{\text{CEX}}_{\text{bid}}(t) and p^{\text{CEX}}_{\text{ask}}(t) denote the CEX bid and ask prices, and let p^{\text{DEX}}(t_n) denote the DEX price at slot n, where t_n = n\tau is the timestamp of slot n and \tau is the slot duration.
Simple Model. In the simple model, the agent attempts to take every detected arbitrage opportunity without regard to execution risk. With probability \alpha, the DEX leg lands successfully, and the agent captures the full arbitrage profit:
With probability 1-\alpha, the DEX leg fails. The agent has already sold on the CEX and must now close the short position. In the simple model, the agent simply buys back on the CEX one second later:
Risk-Averse Model. The risk-averse model endows the agent with two capabilities absent from the simple model: selective entry based on risk-adjusted expected profit and optimal fallback decision when trades fail.
Entry decision. The agent enters an arbitrage opportunity only if the risk-adjusted expected profit exceeds a threshold \theta:
where:
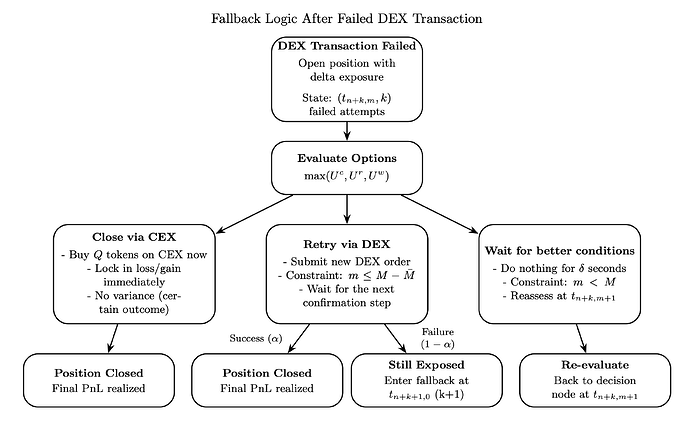
Fallback logic. When the DEX leg fails, the agent holds an open CEX position that must eventually be closed. At each decision point t_{n+k,m} (at slot n+k, subslot m) after k failed DEX attempts, the agent chooses among three options:
- Close immediately: Buy back on the CEX at the current ask price.
- Retry on DEX: Submit a new DEX buy order at the current DEX price and wait for the next slot.
- Wait: Do nothing for one time step and reassess at t_{n+k,m+1}.
The agent selects the option with the highest risk-adjusted utility:
subject to constraints: retry is only available if there is sufficient time before slot end (m \leq M - \bar{M}), wait is only available within a slot (m < M), and after \bar{k} failed attempts, the agent must close.
Computational approach. We solve the value function by backward induction with Monte Carlo estimation at each node. The terminal condition is forced closure at k = \bar{k}. Recursion proceeds in two nested loops: an outer loop over failed attempts (k = \bar{k}-1, \ldots, 0) and an inner loop over subslots within each slot (m = M, \ldots, 0). At each state, we simulate N price paths to estimate the expectation and variance of each option, and then select the option with the highest risk-adjusted utility.
Price dynamics for expectation computation. We assume CEX log-returns follow a Gaussian random walk:
with bid and ask prices given by p^{\text{CEX}}_{\text{bid}} = (1-\beta) p^{\text{CEX}}_{\text{mid}} and p^{\text{CEX}}_{\text{ask}} = (1+\beta) p^{\text{CEX}}_{\text{mid}} where \beta is the half-spread.
Competition Structure
The simulation models the competitive dynamics between agents operating CEX-DEX arbitrage bots. Agent 1 represents the participant whose behavior we analyze in detail, while Agent 2 represents the aggregate behavior of all other market participants. When an arbitrage opportunity arises, multiple agents might attempt to capture it, but blockchain constraints ensure only one transaction can succeed. When Agent 1 attempts an opportunity, they win with probability \alpha. When Agent 1 fails or chooses not to attempt their DEX transaction, Agent 2 automatically succeeds and captures the arbitrage profit.
3.2 Impact on transaction frequency
We measure transaction frequency as the number of transactions landed by the agent. In the simple model, transaction counts increase substantially across all pools. Across all configurations and fee tiers, the simple model exhibits increases ranging from 218% to 663%. The risk-averse model exhibited an even greater increase in transaction frequency, with a transaction count increase ranging from 294% to 1386%. However, it is important to note that most scenarios fall below an increase of 600% with the 1386% being present in a single configuration where, while the percentage change is big, the absolute number of transactions is quite small.
The pattern across fee tiers reflects the economics of arbitrage at different spread levels. Lower-fee pools have tighter spreads and more marginal opportunities. Under a 12-second confirmation, many of these opportunities are not worth pursuing because the execution window is long enough that adverse price moves can wipe out the slim profit margin. Under 1-second confirmation, the risk is compressed, and more marginal opportunities become viable.
Simple agent (weighted average across pools):
| Configuration | \Delta ETH Vol. | \Delta Txns |
|---|---|---|
| no reversion, no noise | +158% | +378% |
| no reversion, noise | +148% | +356% |
| reversion, no noise | +211% | +412% |
| reversion, noise | +188% | +387% |
Risk-averse agent (weighted average across pools):
| Configuration | \Delta ETH Vol. | \Delta Txns |
|---|---|---|
| no reversion, no noise | +159% | +378% |
| no reversion, noise | +163% | +503% |
| reversion, no noise | +212% | +437% |
| reversion, noise | +243% | +567% |
The weighted average of transaction number increase across different pools varies between 356% and 412% for the simple model depending on the configuration, with the average of noise with and without reversion configurations being 371%. Similarly, for the risk-averse model, the weighted increase varies between 378% and 567%, with the average of two configurations being 535%.
Decomposition of effects
The 535% increase in transactions for the risk-averse agent can be actually decomposed into two channels. The simple agent achieves a 371% increase purely from increased composability: more frequent confirmation opportunities allow agents to identify and attempt more arbitrage opportunities within each slot. The additional 164 percentage points arise from de-risking*:* faster confirmations compress the variance of price outcomes during the fallback periods, causing the risk-adjusted expected profit to exceed the entry threshold more frequently.
3.3 Impact on trading volume
Trading volume, measured in terms of Ethereum, shows more nuanced patterns than changes in number of transactions. In the simple model, the volume changes exhibit increases ranging from 98% to 273% depending on the configuration. Similarly to the trading frequency, the increase is closer to the lower end of the range for the 30 basis point pool and closer to the higher end for the 5 and 1 basis point pools. The risk-averse model showed similar patterns with increases ranging from 121% to 375%.
The volume increases are concentrated in lower-fee pools. The intuition here is as follows: when more marginal opportunities become viable, the average trade size may fall (as marginal opportunities tend to have smaller optimal trade sizes), but the total number of trades increases by enough to raise aggregate volume. In higher-fee pools, where opportunities are already large and infrequent, faster confirmations do not as dramatically expand the viable opportunity set.
It is important to note that these ranges represent outcomes under different configurations; however, since gas fees are not incorporated into the model, the upper bounds of these ranges might overestimate the increase for the 1-basis-point and 5-basis-point pools, where the economic viability of frequent small transactions would be constrained by transaction costs in practice.
When weighing the volume increases based on the arbitrage volume across different pools, the average increase in volume for the three pools varies between 148% and 211% for the simple model, with the average being 168%. Similarly, for the risk-averse model, the overall increase varies between 159% and 243%, with the average being 203%.
3.4 Detailed results by pool
Simple agent (30 bps pool):
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +113% | +118% | +116% | +294% |
| no reversion, noise | +97% | +98% | +97% | +218% |
| reversion, no noise | +276% | +273% | +265% | +663% |
| reversion, noise | +218% | +211% | +205% | +478% |
Simple agent (5 bps pool):
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +138% | +158% | +157% | +308% |
| no reversion, noise | +135% | +151% | +150% | +274% |
| reversion, no noise | +147% | +174% | +172% | +345% |
| reversion, noise | +144% | +165% | +164% | +313% |
Simple agent (1 bp pool):
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +195% | +203% | +202% | +420% |
| no reversion, noise | +207% | +200% | +199% | +408% |
| reversion, no noise | +207% | +205% | +204% | +432% |
| reversion, noise | +212% | +202% | +201% | +420% |
Risk-averse agent (30 bps pool):
Note: For the table below, it is important to note that while the changes in the number of transactions in terms of percentages are great for certain configurations, the numbers are small in absolute terms.
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +114% | +121% | +119% | +294% |
| no reversion, noise | +119% | +126% | +124% | +336% |
| reversion, no noise | +282% | +274% | +267% | +639% |
| reversion, noise | +365% | +375% | +365% | +1386% |
Risk-averse agent (5 bps pool):
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +135% | +158% | +157% | +307% |
| no reversion, noise | +137% | +162% | +161% | +444% |
| reversion, no noise | +145% | +174% | +173% | +345% |
| reversion, noise | +147% | +179% | +178% | +500% |
Risk-averse agent (1 bp pool):
| Configuration | \Delta PnL | \Delta ETH Vol. | \Delta USDC Vol. | \Delta Txns |
|---|---|---|---|---|
| no reversion, no noise | +151% | +205% | +204% | +419% |
| no reversion, noise | +151% | +205% | +205% | +544% |
| reversion, no noise | +158% | +208% | +207% | +472% |
| reversion, noise | +161% | +206% | +206% | +554% |
3.5 Robustness analysis
To assess the robustness of these findings, we conducted an additional set of simulations for the risk-averse model under the reversion and noise trading configuration. We varied Agent 1’s win probability \alpha \in \{0.20, 0.35, 0.50\} and the risk aversion parameter \lambda \in \{0, 0.01, 0.03\}, and compared outcomes when the confirmation interval is reduced from 12 seconds to 1 second.
In the 5 basis point pool, across all combinations in this grid, transaction counts increased by 416–530%, and ETH trading volume increased by 146–186%. In the 30 basis point pool, transaction counts increased by 1152–1468%, and ETH volume changes ranged between a 317% increase and a 385% increase.
Overall, changes in transaction counts and volume are of the same magnitude when comparing agents with identical parameters under 12-second versus 1-second confirmation intervals, suggesting that the main results are robust to reasonable variations in win probability and risk aversion.
4. Discussion and next steps
This research examines how reducing blockchain execution times affects decentralized exchange activity, focusing on the behavior of CEX-DEX arbitrageurs. Our contribution is as much methodological as empirical: we develop a simulation framework combining empirical price anchoring, noise-trading dynamics, CEX–DEX arbitrage mechanics, and a risk-averse decision model. The agent we model takes execution risk seriously, incorporating DEX transaction uncertainty into both entry decisions and fallback strategies. This setup captures a fundamental reality of on-chain trading that prior work has largely abstracted away.
Under reasonable assumptions about agent risk preferences and inclusion probabilities, the shift from a 12-second to a 1-second execution environment increases the number of arbitrage transactions by 535%, with effects concentrated in lower-fee pools where marginal opportunities become newly viable. Faster execution also reduces profit variance by compressing the window for adverse price moves during failed-trade recovery.
Limitations. Several limitations are worth mentioning. Our model assumes zero gas fees, which may overstate the viability of small trades in low-fee pools. Also, the agent’s probability of landing DEX trades is fixed rather than endogenously determined by competition; in equilibrium, faster execution might attract more arbitrageurs and compress \alpha. These extensions remain for future work.