Selfish Mixing and RANDAO Manipulation
TL;DR: It’s a known fact that Ethereum’s randomness, which is responsible for crucial tasks such as selecting proposers, can be influenced by validators for personal benefits. In the following, I provide some statistics and simulations showing that, for example, Lido could have gotten 16 slots in epoch 184871 (instead of just 7) by deliberately missing slots two epochs before. Besides, there would have been other cases where “grinding the RANDAO” could have led to economically advantageous outcomes for the manipulating entity. Nevertheless, such behavior can be detected and potentially countered with a social slashing.
Table of Contents:
- Intro into RANDAO
- Some Statistics and Theory
- Simulation based on historical data
- Conclusion & VDFs as a potential solution
Intro into RANDAO
Randomness is a critical component in Ethereum. Many processes such as selecting proposers, assigining validators to commitees or getting selected to participate in a sync commitee rely on the fairness of Ethereum’s random number generator, the RANDAO.
The randomness for the RANDAO comes from validators signing the current epoch number using their BLS secret key. The result is then hashed and XOR’ed into the current RANDAO value. Empty slots without blocks cannot update the RANDAO value.
The RANDAO value required to assign duties in epoch N_t is generated at the last slot of epoch N_{t-2}. This gives proposers, attesters, and sync committee members enough time to prepare for their tasks.
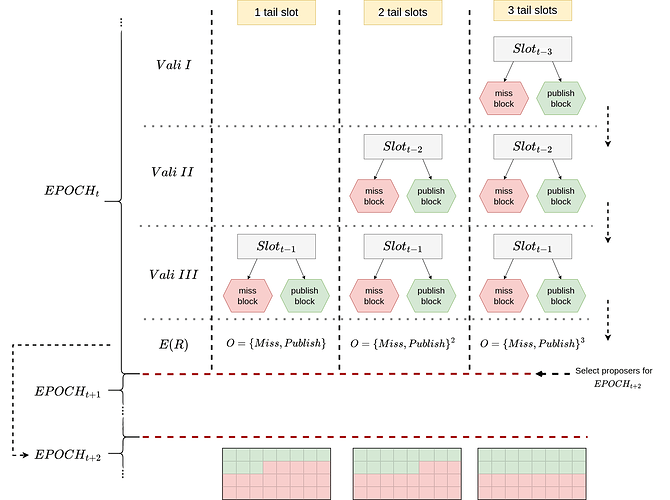
Large validators have more impact on the RANDAO than small ones. They could strategically choose whether to reveal their number (randao_reveal)—or strategically choose not to do so—in order to influence the final random value that is used for selecting block proposers in the future. Notably, this only makes sense for (consecutive) tail-slots which are those at the end of an epoch.
Exploiting this, manipulating validators could be assigned more slots for proposing blocks than usual, earning more rewards and increasing their influence over the network.
In the following post, I want to briefly outline “Selfish Mixing”, a strategy that aims to maximize profits by strategically missing certain slots to avoid updating the RANDAO. The goal is to get more slots allocated in the next but one epoch. The same strategy could also be used to get even more tail-end slots in an upcoming epoch or to get a specific slot in which, for example, an ICO or NFT mint takes place, or another specific event happens.
For further details on randomess on Ethereum, I highly can recommend Ben 's eth2book, in particular the section on Randomness, which covers some potential attack vectors and related statistics on RANDAO manipulation already. Furthermore, Vitalik’s Annotated Specs has a great section on that topic that I can strongly recommend.
Theory and Statistics
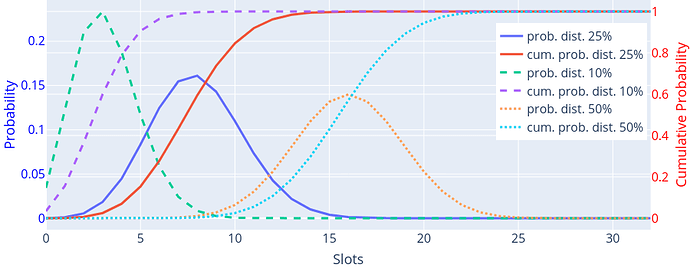
In the following scenario, we’ll assume control of approximately 25% of the validators, all of whom stake the maximum effective balance of 32 ETH.
When controlling a percentage S% of the stake - denoted as p = \frac{S}{100}, the expected number of assigned slots follows a binomial distribution. The probability of getting k slots assigned out of the next n slots can be calculated as follows:
for k = 0, 1, 2, …, n, and a binomial coefficient of
For instance, the likelihood of being granted permission to propose the block for the first slot in the upcoming epoch is simply represented as p. The following plot shows the probability distributions having 10%, 25% and 50% of the total validators:
If an entity controls 25% of the total stake, it can expect to have, on average, eight slots per epoch.
Now, if a validator has access to a single tail-slot of epoch N_t, there are two potential methods for impacting the RANDAO:
(1) Sign the current epoch number, hash, and reveal it (by attaching a block to the chain).
(2) Deliberately miss the slot, thereby not contributing any new random entropy.
Option 2 involves a trade-off, as it means forgoing any rewards (both EL and CL rewards). However, the validator may improve its position in epoch N_{t+2} by having more slots assigned, leading to potential economic benefits.
The level of control an entity has over tail-end slots directly influences its capacity to affect outcomes. Essentially, the more tail-end slots under control, the larger the array of opportunities to sway results.
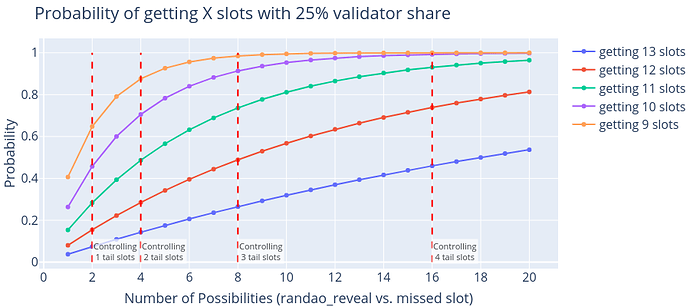
Doing the math, the probability of acquiring a minimum of 9 slots in epoch N_{t+2} is given by:
With this, we can calculate that an entity having 25% of the validators will have a roughly 40% chance of being assigned at least 9 slots.
As shown in the following chart, having more opportunities to impact the RANDAO significantly bolsters the chances of experiencing a favorable outcome. The x-axis shows the number of possibilities, which increases exponentially (2^x) with the number of tail-end slots. For example, having 25% of the validators and 2 tail-end slots in epoch N_{t}, the probability of getting at least 10 slots in epoch N_{t+2} is around 70%. This means that a manipulator, who would normally expect 8 slots, can afford to miss one slot for manipulation and still increase the total number of slots allocated within 3 subsequent epochs.
Looking at the data
First, let’s look at the number of subsequent tail-end slots (those at the end of the epoch) the largest validating entities had in the past (since the merge):
| entity | 1 slot | 2 slots | 3 slots | 4 slots | 5 slots | 6 slots | 7 slots | 8 slots |
|---|---|---|---|---|---|---|---|---|
| lido | 18586 | 5046 | 1432 | 374 | 108 | 35 | 8 | 2 |
| coinbase | 7848 | 978 | 139 | 23 | 1 | 0 | 0 | 0 |
| kraken | 4332 | 302 | 24 | 0 | 0 | 0 | 0 | 0 |
| binance | 3883 | 251 | 11 | 2 | 0 | 0 | 0 | 0 |
| stakefish | 2211 | 73 | 2 | 1 | 0 | 0 | 0 | 0 |
| staked[.]us | 1693 | 45 | 0 | 0 | 0 | 0 | 0 | 0 |
| bitcoin suisse | 1544 | 35 | 1 | 0 | 0 | 0 | 0 | 0 |
| rocketpool | 1512 | 33 | 0 | 0 | 0 | 0 | 0 | 0 |
| figment | 1578 | 32 | 0 | 0 | 0 | 0 | 0 | 0 |
| abyss finance | 614 | 10 | 0 | 0 | 0 | 0 | 0 | 0 |
| celsius | 659 | 7 | 0 | 0 | 0 | 0 | 0 | 0 |
| okx | 329 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| frax finance | 260 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Significantly, Lido had two instances where it controlled eight consecutive slots at the end of an epoch. These events occurred at epoch 149818 and 184869. However, it’s important to understand that Lido is not a singular entity but is comprised of 30 distinct node operators who operate independently from each other. At the time of this writing, Lido holds approximately 30% of the total number of validators. If hypothetically treated as a singular entity controlling the corresponding signing keys, this would have offered Lido 2^8 (256) potential ways to influence the RANDAO for personal economic benefits.
Simulating Potential Impact
Goal 1: More proposers
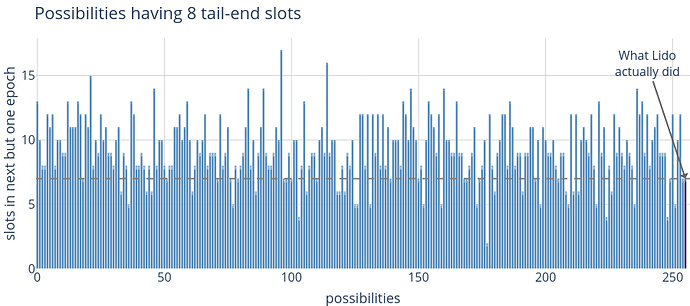
For the following “what-if” simulation, I used the consensus specs to simulate the potential scenarios that an entity controlling eight consecutive tail-end slots at the mentioned epoch at 184869 might have. To do so, I took the beacon chain state at slot 5915831 from a Lighthouse node and then ran through all the 256 possible outcomes.
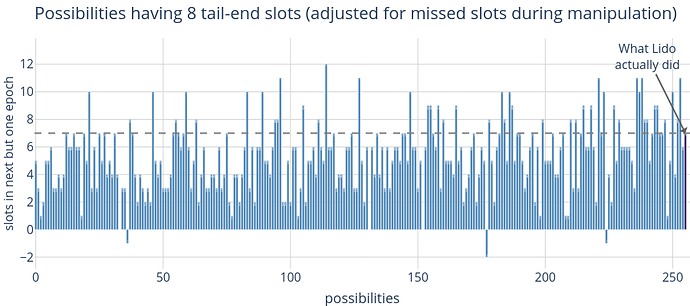
The chart below displays all available strategies along with the selected strategy that, in this case, Lido followed. This involved proposing a block in each of the tail-end slots and not missing a single one - displayed at the most-right on the x-axis with a different color.
It’s evident that there are numerous strategies that could lead to more assigned slots in epoch N_{t+2}. However, these strategies come with a trade-off, requiring the deliberate missing of certain slots. Therefore, we need to adjust the chart to account for these missed slots accurately.
As shown above, the strategy Lido employed didn’t yield any changes, as no slots were missed within the eight tail-end slots. It can already be deduced from the chart that Lido could have improved its own position through a different strategy.
The table below outlines the most beneficial alternative strategies that could have led to an increased count of up to 9 additional proposers in epoch N_{t+2}. To describe the different strategies, I’ll use a binary code where 0 denotes a missed slot and 1 stands for a slot with a randao reveal. This is in comparison to the seven proposers that Lido actually had in N_{t+2} (epoch 184871):
| strategy | # of proposers in N_{t+2} | adjusted # of proposers in N_{t+2} |
|---|---|---|
| 0 1 1 1 0 0 1 0 | 16 | 12 |
| 0 1 1 0 0 0 0 0 | 17 | 11 |
| 0 1 1 1 1 1 1 1 | 12 | 11 |
| 1 1 0 1 1 1 0 1 | 13 | 11 |
| 1 1 1 0 1 1 0 0 | 14 | 11 |
| 1 1 1 0 1 1 1 0 | 13 | 11 |
| 1 1 1 1 1 1 0 1 | 12 | 11 |
The optimal strategy, denoted by (0\ 1\ 1\ 1\ 0\ 0\ 1\ 0), would have required missing 4 out of the 8 slots in epoch N_{t} (epoch 184869). This sacrifice, however, would have secured a whopping 16 slots in epoch N_{t+2}, thereby maximizing influence in that epoch.
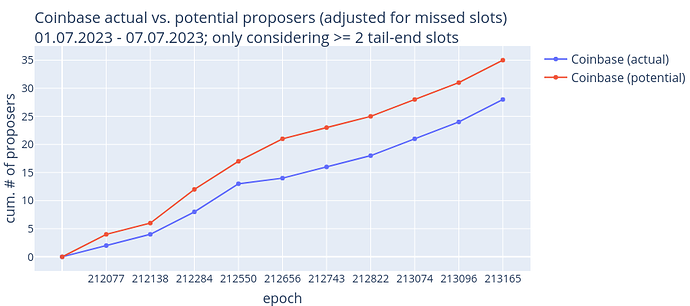
As mentioned, Lido’s validators aren’t controlled by one entity but by multiple node operators. This is not the case for the validators of Coinbase, Kraken, Binance, Stakefish, etc. Thus, let’s look into the potential of RANDAO manipulation by these ‘smaller’ entities. The following covers Coinbase, which is currently, after Lido, the second largest staking entity, controlling 7-8% of the total validators. The chart below compares Coinbase’s actual performance in the first week of July '23, measured in the number of proposers vs. the potential number of proposers when maximally grinding the RANDAO:
We can see that although Coinbase could have had 7 more proposers in that week, the impact is relatively low compared to their total expected number of proposers in one week, which is 3528 (assuming a 7% share). Notably, I have only considered epochs in which Coinbase had at least four opportunities (two tail-end slots) to influence the RANDAO mix, disregarding epochs where they faced a binary choice by controlling only a single tail-end slot.
In times of high MEV, this might still be worthwhile, not taking into account the potential reputational damage.
Goal 2: Getting a specific slot
Second, I aim to evaluate whether manipulating RANDAO could be advantageous for securing a specific slot in epoch N_{t+2}. This might be particularly useful if there’s an upcoming ICO or NFT mint that the manipulating entity wishes to participate in.
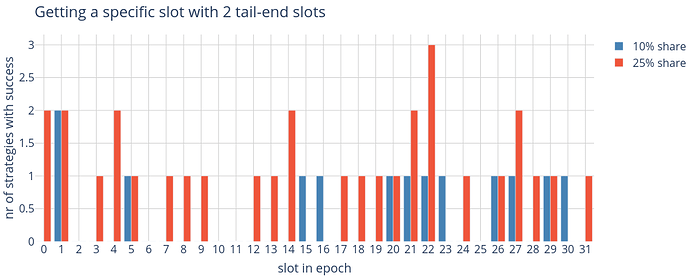
The following shows the potential slots in epoch N_{t+2} (epoch 184871) that an entity (Lido), which has access to two tail-end slots, could get:
Depending on the proportion of validators under its control, it becomes clear that such a manipulating entity - with four different outcomes based on the specific strategy - has substantial influence over the precise slots it might attain. With a share of 25% of the validators and having 2 tail-end slots in the epoch N_{t}, the entity could influence the RANDAO to get 23 different slots in epoch N_{t+2}. With 10% share, this reduces to 12 slots.
Conclusion, Threats and Solutions
In conclusion, this analysis explored the concept that the binary choice - either revealing the pseudorandom ‘randao_reveal’ value or intentionally missing a block, thereby leaving the RANDAO value unchanged - can be exploited for personal gain.
The analysis further implies that relying on the RANDAO for applications on the execution layer, especially where economic outcomes are dictated by the RANDAO’s randomness, may not be the wisest approach. For instance, a smart contract casino that uses the RANDAO to draw winners could potentially fall prey to a proposer who manipulates the RANDAO for their personal advantage in a subsequent round. This same vulnerability also applies to games such as FOMO3D, which are built on the premise of fair access to block space for every player.
If an entity were to engage in large-scale RANDAO manipulation, it could likely be detected and would very probably be perceived as an unfair attack on the network. This could potentially lead to a social-slashing event.
The solutions to this issue have already been discussed - namely employing Verifiable Delay Functions (VDFs). VDFs are like digital puzzles that take a certain amount of time to solve, no matter how much computing power you have. They require a certain amount of time to compute, but once the solution is found, anyone can quickly verify that it’s correct. Getting the RANDAO mixes from a VDF would prevent manipulators from grinding RANDAO values that benefit themselves.
However, as of this writing, there are no concrete plans to implement this solution.
Finally, find the code used for this analysis in this repo.
Furthermore, find additional content on that topic from Vitalik and Justin in this ethresearch post, as well as the rdao-smc Github repo providing a formal probabilistic model of RANDAO-based Random Number Generation.
If you prefer video format, Justin talks about randomness, covering VDFs, here.