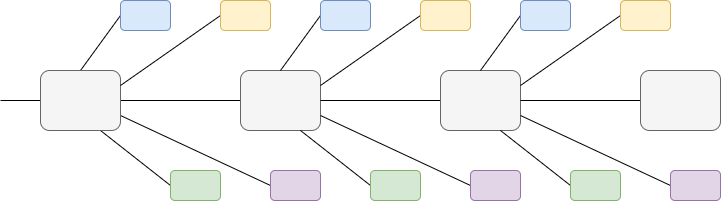
One of the ideas that becomes possible with sharding is the concept of staggering: having shards produce blocks at different times, allowing the system as a whole to have blocks at a regular frequency of more than one per second. Layer-2 projects (eg. rollups) built on top of this system could then have latencies on the order of a second or lower, despite the system as a whole having 12-second latencies.
The four colors represent four shards; each shard and the beacon chain have a latency of k seconds, but the system as a whole has a block appearing once every \frac{k}{4} seconds.
A significant challenge in implementing this, however, is incentives. Even if we add a protocol rule that shard proposers are “supposed to” publish their shard blocks at asymmetric times (eg. shard 0 publishes 1/8 after the start of a slot, shard 1 publishes 3/8 after the start of a slot, etc), the “supposed to” matters little if there are no actual protocol rules that ensures that this actually happens.
There are incentives that govern when block producers publish blocks: if you publish too early, you miss out on transactions, if you publish too late, you risk the block not getting included, and somewhere in the middle is the optimum. If we want shard blocks to be staggered, we need incentives that differ between shards so that the optimal publishing time is staggered too.
Let N = 64 be the number of shards. Let D = [8, 16, 24, 32] be a list of distances. Define an “optional ancestry link” as a link from the (k - D[i])'th header to the k'th header (the z'th header here means the header of shard k\ mod\ N in slot \lfloor \frac{z}{N} \rfloor).
Dotted lines represent optional ancestry links for N = 4 and D = [2, 3].
Idea 1: one byte per optional ancestry link in the header
We add to the shard header an “ancestry checksum” with |D| bytes: byte i of the k'th header is expected to be the same as the first byte of the hash of the (k - D[i])'th header. So for each optional ancestry link, there is a one-byte slot to include the first byte of the hash of the ancestor block.
These ancestry checksums being correct is not necessary for validity; it’s okay for shard headers to provide an ancestry checksum with some or all bytes being invalid. Rather, we add incentives to encourage them to be correct, without mandating it.
Note also that instead of requiring a shard block at slot N to reference the beacon block at slot N and be eligible for inclusion in slot N+1, we move the inclusion slot up to N+2. This allows shard blocks to be published around the same time as the beacon blocks themselves, so there is no “hole” in shard block progression around the time when beacon blocks get proposed.
Idea 2: one hash per optional ancestry link in the body
The first D chunks of a shard header body are reserved for ancestry links. Specifically, the i'th chunk of the k'th shard block is expected to be the same as the hash of the (k - D[i])'th header.
These hashes being correct is not necessary for validity; rather, we add incentives to encourage them to be correct, without mandating it.
Idea 3: checksum based on contents instead of header
Notation note: “[W]” means “a Kate commitment to the polynomial W”, e(a, b) is a pairing.
Let P be the polynomial committed to by the (k - D[i])'th header, and let z be the proposer’s private key. The first chunk of the shard block body is expected to equal P(z). Note that this is a linear function of the entire shard block body, and it requires the entire body to calculate.
It can easily be proven with a Kate proof: let Q(X) = P(X) // (X - z), where [Q] can be verified by checking e([X - z], [Q]) = e([P - c], [1]) where c is the claimed value. [X-z] can be computed as [X] - Z where Z is the proposer’s public key (so verification can be done publicly).
Using a function of the shard block body and the proposer’s private key ensures that the proposer needs to download and check the entire shard block body, and encourages the proposer of the older block to actually publish the data quickly. This mechanism does require the proposer to get on a few extra shards when they get assigned to propose, but it only affects the proposer so total impact on validator node complexity is low.
Ancestry checksum incentives
The core incentive in all three cases is simple. If a shard block correctly includes an optional ancestry link to another shard block, then we add a probabilistic lottery: based on some future RANDAO value, there is a \frac{1}{X} chance that a reward of size proportional to X is applied to both the producer of the shard block that included the link and the producer of the shard block that was included.