This document describes a maximally simple version of single secret leader election (SSLE) that still offers good-enough diffusion of the likely next location of the proposer. It relies on size-2 blind-and-swap as a code primitive. Size-2 blind-and-swap proves that two output commitments (OL1, OR1), (OL2, OR2) are re-encryptions of two given input commitments (IL1, IR1), (IL2, IR2), without revealing which is a re-encryption of which. The shuffle protocol uses a large number of these blind-and-swaps to shuffle a large number of commitments. Eventually one of these commitments is picked to be the proposer. The proposer would need to reveal themselves to “claim” this opportunity, but until the moment the block is published, no one knows who the proposer is; simply looking at the shuffle network would lead to hundreds of possible nodes that you need to take down in order to have even a 20% chance of taking down the next proposer.
Parameters
| Parameter | Recommended value | Notes |
|---|---|---|
WIDTH |
2048 |
|
SWAP_TREE_DEPTH |
5 |
2**depth - 1 swaps per slot |
Construction
We maintain in the state an array of blinded commitments: blinded_commitments: Vector[BlindedCommitment, WIDTH]. We also add to the Validator struct extra fields that allow a “fresh” (ie. not yet mixed/blinded) BlindedCommitment for a given validator to be generated. We initialize the array with fresh commitments from a randomly picked set of validators.
During each slot, we use public randomness from the randao_reveal to pick three indices:
proposer_blinded_index(satisfies0 <= proposer_blinded_index < WIDTH)fresh_validator_index(is an active validator, eg. member 0 of committee 0)shuffle_offset(an odd number2k + 1where0 <= k < WIDTH / 2)
We allow the validator who owns the blinded commitment at blinded_commitments[proposer_blinded_index] to reveal the commitment to propose the block at that slot. The proposer’s blinded commitment is replaced by a fresh blinded commitment from validators[fresh_validator_index].
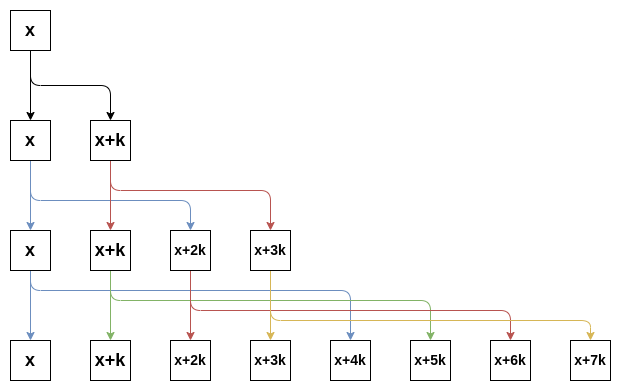
Finally, we perform the shuffling tree mechanism. The goal of the shuffling tree is to do a series of N-1 swaps that spread out the possible location of the freshly selected validator evenly across N possible locations, where N = 2**SWAP_TREE_DEPTH, in addition to further spreading out the possible locations of other proposers that end up in the shuffle tree. The shuffle tree of a given slot is based on the proposer_blinded_index and shuffle_offset at each slot, and looks as follows:
At depth 0, we do a swap between x and x+k. At depth 1, we do a swap between x and x+2k and another swap between x+k and x+3k. At depth 2, we do four swaps, one between x and x+4k, the next between x+k and x+5k, and so on. If, at the beginning, the validator at position x was known to be N, after running the full shuffle tree up to this point, the possible location of N could be anywhere in (x, x+k ... x+7k), with a 1/8 probability of being at each spot.
Because the WIDTH of the buffer of blinded commitments is limited, we wrap around. For example, the swaps involved in the shuffle tree for (x = 8, k = 3) would look as follows:
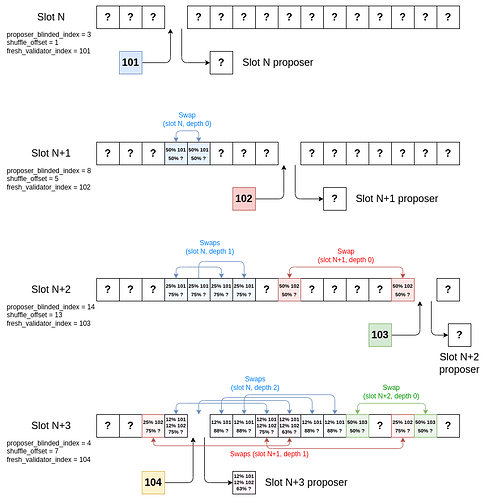
To ensure robustness, we don’t do a any single shuffle tree entirely within each slot. Instead, we stagger the shuffle trees. That is, we do the depth 0 layer of the slot k shuffle tree in slot k+1, the depth 1 layer of the slot k shuffle tree in slot k+2, etc. This ensures that if any single validator is malicious and reveals their swaps to an attacker, the minimum anonymity set of a proposer is only decreased from 2**SWAP_TREE_DEPTH to 2**(SWAP_TREE_DEPTH - 1).
Here is what a few rounds of the whole process would look like, tracking the probability distributions of which validators could be in which positions. For example, “50% 101, 25% 102, 25% ?” means “there’s a 50% chance this commitment is validator 101, a 25% chance it’s validator 102, and a 25% chance it’s someone else”.
Code specification of get_swap_positions
def get_swap_positions_at_depth(pivot: uint64, offset: uint64, depth: uint64) -> List[Pair[uint64, uint64]]:
output = []
for i in range(2**depth):
L = (pivot + offset * i) % WIDTH
R = (pivot + offset * (i + 2**depth)) % WIDTH
output.append((L, R))
return output
def get_swap_positions(state: BeaconState) -> List[Pair[uint64, uint64]]:
output = []
for depth in range(SWAP_TREE_DEPTH):
randao_at_depth = get_randao(state, state.slot - depth - 1)
proposer_blinded_index = randao_at_depth[:8] % WIDTH
shuffle_offset = randao_at_depth[8:16] % (WIDTH//2) * 2 + 1
output.extend(get_swap_positions_at_depth(proposer_blinded_index, shuffle_offset, depth))
return output
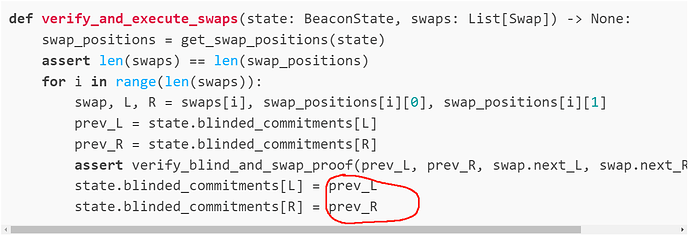
Code specification of verify_and_execute_swaps
def verify_and_execute_swaps(state: BeaconState, swaps: List[Swap]) -> None:
swap_positions = get_swap_positions(state)
assert len(swaps) == len(swap_positions)
for i in range(len(swaps)):
swap, L, R = swaps[i], swap_positions[i][0], swap_positions[i][1]
prev_L = state.blinded_commitments[L]
prev_R = state.blinded_commitments[R]
assert verify_blind_and_swap_proof(prev_L, prev_R, swap.next_L, swap.next_R, swap.proof)
state.blinded_commitments[L] = prev_L
state.blinded_commitments[R] = prev_R
Note that get_swap_positions may create swaps that overlap with each other. For this reason, it’s important to implement verify_and_execute_swaps as above, executing the swaps from first to last in order.
Simulation results
There is a script here that can run many rounds of the shuffle tree mechanism, and outputs the 20%-diffusion of the proposer location. This refers to the number of validators that an attacker would need to take offline (eg. with a targeted DoS attack) to have a 20% chance of taking down the proposer.
Here are some results. The values are given in pairs, where the left value is the average 20%-diffusion and the right value is the probability that the 20%-diffusion equals 1 (meaning that you only need to take down one validator to have more than a 20% chance of taking down the proposer).
| Swaps = 7 | 15 | 31 | 63 | |
|---|---|---|---|---|
| Width = 32 | (2.66, 0.20) | (4.43, 0.12) | (5.07, 0.036) | - |
| 64 | (3.02, 0.118) | (7.08, 0.102) | (9.53, 0.040) | (9.79, 0.028) |
| 128 | (3.13, 0.044) | (10.3, 0.056) | (18.8, 0.024) | (20.0, 0.020) |
| 256 | (3.13, 0.012) | (13.72, 0.046) | (36.0, 0.018) | (42.8, 0.022) |
| 512 | (3.02, 0.014) | (17.26, 0.01) | (65.31, 0.008) | (89.7, 0.004) |
| 1024 | (3.03, 0.009) | (19.23, 0.005) | (114, 0.004) | (177, 0.006) |
| 2048 | (2.98, 0.006) | (20.80, 0.005) | (194, 0.004) | (347, 0.004) |
The cost to increasing the WIDTH is relatively low; the main downside of an extremely large buffer is that it increases the chance of a missing proposer because by the time a validator is selected they have already left the validator set. Assuming a withdrawal time of 8192 slots (~1 day), this implies a maximum “reasonably safe” buffer width of around 1024-2048 (2048 would ensure that if a validator exits immediately after being added to the buffer, they would only get a wasted post-exit proposal opportunity less than 2% of the time). 31 swaps seems to be the minimum required to get a large amount of diffusion, and 63 swaps gives near-perfect diffusion: the 20%-diffusion set is close to 20% of the WIDTH, which is what you would get if you just shuffled the entire buffer in each slot.
Each Swap in the BeaconBlock takes up 7 elliptic curve points (2x BlindedCommitment + 3 curve points in the proof), so 336 bytes. Hence, 31 swaps would take up 10416 bytes. Switching to a 32-byte curve would reduce this to 224 * 31 = 6944 bytes. Verifying a blind-and-swap takes 4 elliptic curve multiplications and 3 size-4 linear combinations. A size-4 linear combination is ~2x more expensive than a multiplication, so this is equivalent to ~10 elliptic curve multiplications. Hence, the total verification complexity is ~310 elliptic curve multiplications (~31 milliseconds).
These facts together drive the choice of WIDTH = 2048 and SWAP_TREE_DEPTH = 5 (31 swaps per block).