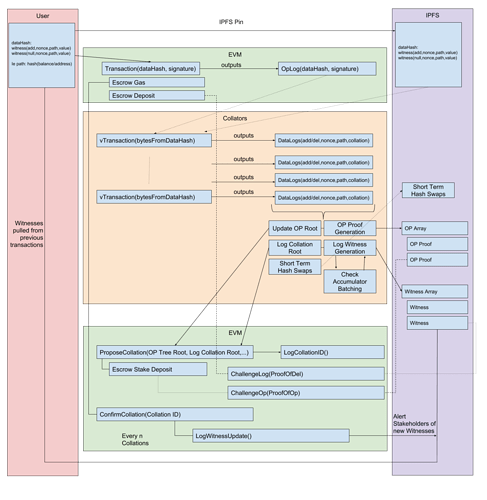
What is in place to keep us from doing this with the current EVM + Collators?
Say we write new contracts where each state-changing function has a corresponding virtual function that is view only. The state changing function does not do any work and only emits an OpLog requesting that a transaction should be performed. It is provided with a data hash and some funds for extra-gas and stake.
Collators see the OpLog and download the data from the datahash(say from IPFS or from some libp2p chatter network). This DataHash contains all the witnesses needed to execute the function ‘for real’, but it doesn’t get executed on the chain. Instead, the collator executes the view only function in whatever off chain client they like. This means we are not limited by max block gas limit. This makes high-cost transactions like snarks or massive air drops much more feasible(if you can get a collator willing to do the collation).
This virtual function does emit data logs(adds and dels) to the collator according to the contract. These logs don’t get appended to the EVM because this is a view function. These logs will be included in the resulting collation. The collator does this for as many OpLogs as it has found in the current time period. Becuase this is an external program it can keep track of short-term hash swaps for witnesses updates such that items can continue to be processed across collations.
Finally, it produces a collation log root that goes into our log accumulator and also updates an Op Patricia Tree with a hash of the OpLog so that we can later prove that this OpLog has already been processed. The collator is also responsible for producing the witnesses for the Datalogs and the proofs for the Op Tree and puts them somewhere they can be retrieved.
These two items are the inputs for proposing a collation. The collation can be challenged with a log proof showing that an add witness was used that already had a del witness invalidating it. A collation can also be challenged with an Op proof that shows the collator submitted an Op that had already been processed. If the collation is invalidated they have to start over or someone else has a turn.
There is some sort of confirmation(Maybe Truebit style challenge game based on random EVM stack challenges, or maybe a form of Casper, or maybe the proofs are enough). Once the collation is committed users can download all the relevant witnesses. We may have a proof of publication problem here, but that may be easily solvable by making the confirmers reassemble a hidden hash. Recommendations on confirmation encouraged.
If the confirmation is successful then the collator and set of confirmers split up the extra-gas provided in the initial transaction.
What major items am I missing?
I do still have concerns that I can’t prove that a value is 0. We may have to have some kind of special witness type for this, but it seems that it might be easy to exploit if someone isn’t paying attention to the whole history.
Which brings me to the question of why not use a Patrica Tree? The tradeoff is that the witnesses need to constantly be updated instead of being updated just once, but if we are using an external program to do that then we should be able to process and publish the hash swaps that need to occur. This table would be a new data set that users would need to sync with to update their witnesses. I have no frame of reference as to what the data size would end up being here, but most of this can all be kept in off EVM storage and queried as needed. If the ‘swaps’ computation gives you an invalid collation buffer then you did something wrong.
I haven’t run this path all the way out yet but I think you could also have contracts that track cross-shard collations as well such that the witnesses from those shards are easy to check. Maybe update the witness inputs to be (networkid,add/del/null,nonce,path,value) or maybe have the network ID be part of the path.
Any and all feedback encouraged. Here is a diagram of the process for discussion. I’d love to spend more time running down this rabbit hole and building out the contracts and collator software, so feel free to point me in the right direction.