There’s desire for more client diversity in the Ethereum ecosystem. Specifically there seems to be room for clients with different capabilities. EthereumJS VM was my entry point for working on the protocol, and I would like to see it become a light client running in the browser one day.
Light clients currently overwhelm altruistic servers and require complicated incentivization models to be sustainable. This problem can be attacked by minimizing the amount of data pulled from servers and where possible replacing that with servers broadcasting data to the network.
Overview
For the purposes of this post we’ll focus on one of the problems light clients try to solve: verify the inclusion of a transaction in the chain and its validity, on a resource-constrained device (equivalent to SPV nodes in Bitcoin). In order to do this check, the light client first needs to determine the canonical chain. The most naive, but secure approach is to download and validate all the block headers of the chain advertised to have the most accumulated difficulty. With the total size of block headers nearing somewhere between 5Gb and ~8Gb (depending on the implementation) this approach is completely infeasible. In LES this is worked around by hardcoding checkpoints in the form of CHTs in the client.
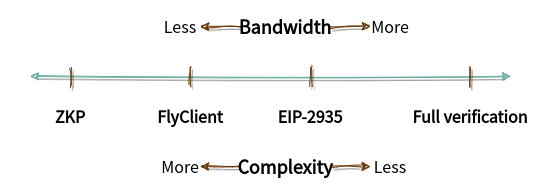
In the rest of this document we’ll go over some alternatives to the status quo. At a high-level these approaches imply different bandwidth requirements and have varying consensus complexity.
ZKP
The goal of this hypothetical approach (similar to the Coda blockchain) is to demonstrate the other end of the spectrum, where blocks include a zero-knowledge proof proving that:
- There exists an unbroken chain of blocks from genesis to the current block
- Block headers are valid according to the consensus rules
- The total difficulty of the chain is a certain value. In the presence of competing forks the light client can verify the proof in each fork’s head block and compare the total difficulty to find the heaviest chain.
What I want you to take away from this is the properties of the ideal approach:
- Short proof: Depending on the exact proof system the bandwidth required is likely less than 1Kb.
- Non-interactive proof: The proofs are so short they can be distributed along with the block. No need for light clients to request any data from servers. Having full nodes respond to light client requests is a massive bottleneck and severely limits the numbers of light clients each full node can serve.
- Guaranteed security: Same as in the naive approach of downloading all block headers, the light client can be sure about the canonical chain.
FlyClient
FlyClient is the state of the art when it comes to the initial syncing for light clients. It was recently activated on Zcash as part of the Heartwood network upgrade. It gives you relatively short proofs (500Kb for 7,000,000 blocks assuming 66% honest mining power according to the paper). These proofs are non-interactive and similar to the ZKP approach can be gossiped in scale. FlyClient is secure with an overwhelming probability. It can further be configured to tolerate more or less dishonet mining power by trading off bandwidth.
This approach requires a consensus change in the form of a new field in the block header. The new field historicalBlocks is the root hash of a tree storing all block hashes from genesis up to the parent block. The tree in question is a modified Merkle Mountain Range (MMR). The Difficulty MMR stores some extra metadata in the nodes of a vanilla MMR. The metadata allows us to verify the aggregate difficulty of all the blocks in the subtree under each node.
Now let’s see how this change helps light clients sync. Assume LC is a light client who performs a network handshake with multiple full nodes FN_i each of which advertise the total difficulty of their best chain and the hash of its head. Some of the full nodes might be malicious. LC sorts the full nodes in descending order of their advertised total difficulty and for each performs the following:
- Fetch and verify the last block
H’s header - Randomly sample log(N) historical blocks
B, for each:- Verify the header (incl. PoW)
- Verify proof against
H.historicalBlocksto make sureB’s hash matches the MMR leaf inH - Verify that
B’s historical blocks are a prefix ofH’s. MMR allows this check to be performed efficiently. However because we can’t modify past blocks, this condition can only performed for blocks after the hardfork that introduces thehistoricalBlocksfield.
The sampling algorithm tries to maximize the chance of finding at least one invalid block in a dishonet chain regardless of the adversary’s strategy. It samples from a smooth probability distribution, with relatively low probability for selecting a block from the beginning of the chain and continuosly increasing probably as you move towards the end of the chain. However to take Ethereum’s variable difficulty in mind, the beginning and end of the chain are not in terms of block numbers, rather in terms of cumulative difficulty. Hence the reason for embedding difficulty information in the tree nodes is to be able to query e.g. the block at 1/2 of the total difficulty.
Each sampling step is separate and doesn’t depend on the result of any other step. Hence the whole process above can be made non-interactive by using a publicly verifiable source of randomness, like the parent block’s hash or drand, as seed for the sampling algorithm. The result is a single proof that a full node can generate independently and broadcast for a host of light clients to verify. The proof shows there exists a connected chain from genesis to the advertised head with the given total difficulty.
EIP-2935
EIP-2935 proposes a simpler consensus change in comparison, which involves storing the hash of historical blocks in the storage slots of a system contract. Light client sync is stated as one of the motivations, along with being able to prove a historical block against only the head of the chain which would be useful in L2 state providing networks. Making the blockhashes explicitly part of the state also helps with stateless block witnesses.
So the question is how can we use this EIP for the purpose of syncing light clients. Here we go into two variants, both of which require the EIP to be modified to store all the historical block hashes since genesis, as opposed to the block hashes since the hardfork block.
Variant 1: Random sampling
I think you can build a protocol which somewhat resembles FlyClient—in that it does random sampling of blocks—on top of this EIP. However it will either have lower probabilistic security if we keep the bandwidth requirement constant, or require higher bandwidth if we want to have the same amount of security as in FlyClient.
First, let’s see the similarities between this variant and FlyClient. The general flow of the protocol will be very similar: Light client fetches the last block header. The state root in the header also commits to the hashes of the historical blocks stored in the blockhash contract (BHC). Therefore the client can verify the hash of a sampled block header by verifying a merkle branch against the storage root of the BHC. Note that if you wanted to sample a subset of the chain today on the mainnet an adversary could return blocks that are not necessarily chained together. Having the adversary commit to a whole chain as EIP-2935 makes these kind of attacks harder.
The major difference between the two approaches lies in the tree structure they use to store the historical block hashes. Two properties that the Difficulty MMR has which the storage trie doesn’t are (among others):
- Each node stores the cummulative difficulty of the blocks in that subtree
- MMR allows efficient subrange check, i.e. checking that two MMRs share the first N leaves. To do this check with the storage trie, you’d have to send all the first N leaves.
Both of these properties make it harder for a malicious actor to deceive a light client. Without the first one, an attacker could craft a chain with a high number of low difficulty but valid (PoW-wise) block headers and insert a few high difficulty but invalid blocks in the middle to raise the total advertised difficulty of the chain. When sampling blocks without knowing the relative difficulties you have less chance of discovering these invalid blocks. When sampling an old block B, the second property allows you to verify that the chain from genesis to B is a prefix of the chain from genesis to the head.
As such we won’t be able to use the same sampling algorithm as in FlyClient. The naive option is of course to do uniform sampling, which requires many more samples to achieve relatively high security. Paul Dworzanski proposed adding the cummulative difficulty to the leaves in the BHC alongside the blockhash, and then do a binary search (similar to section 5.2 in the FlyClient paper) over the blocks, zooming in on subchains that have suspicious difficulty. Overally the sampling strategy to use in combination with this EIP, its bandwidth requirement and security guarantees are open problems.
Variant 2: Superblock-based
An alternative variant to random sampling was suggested by the author of EIP-2935:
Make a subchain containing only blocks passing 1000x the difficulty threshold, with those blocks linked to each other through the history contract.
You might remember that each Ethereum block has a difficulty threshold that a PoW solution must surpass. Sometimes the PoW solution is higher than the threshold by a large margin. Since hashes are uniformly random, a PoW solution with a value double that of the threshold has 1/2 chance of occuring compared to a solution barely above the threshold.
Similar to NiPoPoW (where I borrowed the term superblock from to refer to these lucky blocks), this approach uses these rare events to “compress” the header chain. Effectively a full node sends all the block headers in the chain where the solution is 1000 times the difficulty target. This should convince a light client that there’s a lot of mining power behind this chain. To choose between forks, light clients count the number of the superblocks in the proof.
With regards to security, let’s set the difficulty adjustment mechanism aside for a moment. Assuming that an adversary controls less than 50% of the mining power, the probability that they produce as many superblocks as the honest chain is very low. But difficulty is not constant in Ethereum. A hypothetical attack is to fork off and bring the difficulty down significantly. Given that downwards difficulty adjustment is capped at ~5%, the attacker could for example bring the difficulty down by a factor of 10^8 in ~350 blocks. Afterwards mining superblocks would be easier. The adversary might require significant mining resources to pull off this attack, but I haven’t estimated how much exactly. To alleviate this we can modify the fork comparison algorithm to be the sum of the actual difficulty of the superblocks in a proof (changed from a simple count of the superblock).
At any time there could be several thousand blocks of distance between the head of the chain and the last produced superblock on the honest chain. To avoid the scenario where an adversary fools a light client by forking off after the last produced superblock, the proof includes the headers for several thousand blocks at the tip. To reduce proof sizes, it should be possible to instead send fewer superblocks of a lower degree, e.g. blocks with 512, 256 and 128 times the difficulty target.
With all this in mind, the size of the proof a full node has to send to a light client was estimated by Vitalik as follows. Note that the parent’s header is required to compute the canonical difficulty, so the first part of the estimate might need to be roughly doubled.
That would be roughly 10000 * (512 block header + 1500 for the proof), so about 20 MB, and then a bit more for the last few thousand blocks in the chain.
Conclusion
To wrap up, we went briefly over the landscape for syncing light clients. From full verification of every block header being one end of the spectrum, and the hypothetical ZKP approach being close to an ideal syncing experience. There are feasible improvements to be found in the middle of the spectrum. If complexity wasn’t an issue FlyClient provides very good trade-offs without sacrificing any of the other use-cases.
The competitor is EIP-2935, with a simpler consensus change, on top of which we can design various light client sync protocols, e.g. via random sampling or superblocks. These protocols might not match FlyClient in some metrics and haven’t been formally analysed, they might however suffice to remove the need for CHTs. A more detailed comparison of the superblock approach and CHTs in terms of bandwidth requirement is still pending. The next concrete step is to define a more precise superblock-based algorithm on top of EIP-2935 and prototype it in a client to get quantitative data.
Acknowledgements: This write-up would not have been possible without discussions and feedback from my teammates Alex Beregszaszi and Paul Dworzanski (from Ewasm), and Vitalik Buterin.